Учебное пособие: Электрические аппараты

За   время энергия, генерируемая в теле, будет расходоваться на повышение температуры тела                 а часть ее                      будет отдаваться в окружающую среду:

(6.30)

Следовательно, уравнение процесса нагрева тела

(6.31)

Частное решение последнего уравнения

 

(6.32)

Общее решение дополнительного уравнения

(6.33)

будет

(6.34)

где А — постоянная интегрирования, определяемая условиями задач.

Величина                       равная отношению полной теплоемкости С тела к его теплоотдающей способности          называется постоянной времени.

Общее решение уравнения:

(6.35)

Для определения постоянной А используем следующее условие: при

 должно быть               значит

(6.36)

Подставляя полученное выражение, будем иметь

(6.37)

На рис.6.6 представлено графическое изображение последнего выражения, из которого видно, что при t = со

(6.38)

Откуда следует, что

(6.39)

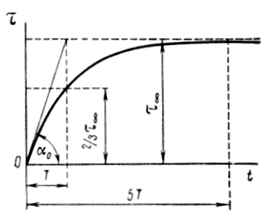
Рис.6.6. Зависимость превышения температуры от времени при нагреве однородного тела

Таким образом, т0 равно установившемуся превышению температуры, когда выделяемая мощность Р становится численно равной мощности, отдаваемой в окружающую среду с поверхности нагретого тела (k^0SxJ).

Очевидно

(6.40)

Из (6.39)следует:

(6.41)

Касательная к кривой  в   начале координат отсекает на прямой too отрезок, равный в выбранном масштабе постоянной времени Т.

Нетрудно показать, что при

(6.42)

На основании этого можно определять постоянную времени Т как время, необходимое для достижения     установившегося превышения температуры (см. рис.6.6).

С точностью                 можно считать, что процесс установления температуры происходит через время, равное

После отключения аппарата начинается его охлаждение. Так как энергия, подводимая к аппарату, равна нулю, то левая часть также равна нулю:

(6.43)

Решение уравнения (6.43) имеет вид:

(6.44)

где А — постоянная интегрирования, равная

(6.45)

Окончательно получаем:

 

Основы теории передачи тепла теплопроводностью

Основной закон теплопроводности био - Фурье

Основной закон теплопроводности математически описывается выражением

(6.46)

Здесь:          количество тепла, передаваемое за время dt

через площадку S в направлении нормали к последней;

 производная от температуры вдоль нормали (п) к

площадке S;

 коэффициент теплопроводности {вт/м°С).

Знак (—) показывает, что тепло передается в направлении убывания температуры вдоль нормали (п) к площадке (S).

Поделив обе части равенства на dt, получим количество тепла, проходящее в единицу времени через площадку S

(6.47)

Производная                         является тепловым потоком через площадку S. Отношение

(6.48)

представляет собой плотность теплового потока в какой-либо точке на поверхности S. Таким образом, равенство можно написать в следующем виде

(6.49)

Передача тепла теплопроводностью сквозь толщу стенки, ограниченную двумя плоскостями

Рассмотрим простейшие случаи, когда тепловой поток Ф и его плотность Ф0 не изменяются во времени (стационарное состояние) и в пространстве.

Такой случай может иметь место при наличии стенки толщиной б, ограниченной двумя параллельными плоскостями и разделяющей две среды (жидких или газообразных) с различными температурами (рис. 6.7).

Пусть температура fli на всем протяжении одной стороны стенки 1 будет больше, чем температура Ь2 на противоположной стороне. Предполагая, что площадь стенки достаточно велика (теоретически не ограничена), можно предположить, что поверхности с одинаковой температурой (изотермические поверхности) в толще стенки будут представлять собой плоскости, параллельные граничным поверхностям, имеющим постоянные (но различные) температуры на всем протяжении каждой поверхности. При этом естественно, что изменение температуры будет происходить только в направлении нормали к поверхности стенки. Вследствие этого, направляя ось ординат вдоль стенки 1, ось абсцисс — вдоль нормали к поверхности стенки, и заменяя букву п буквой х в равенстве можно написать:

Этому дифференциальному уравнению соответствуют следующие граничные условия:

Решением уравнения будет

(6.50)

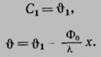Для определения Сх используем условие:

т. е.

Из последнего равенства следует, что температура в стенке изменяется по закону прямой.

Используя условие получим:

т. е.

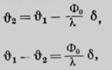(6.51)

где                       падение (перепад) температуры в толще стенки при данной плотности теплового потока.

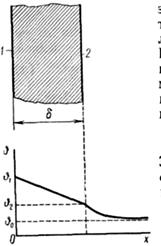
Рис.6.7. К расчету теплопередачи через плоскую стенку

Формулу (6.51) пишут иначе, учитывая, что

(6.52)

Следует обратить внимание на аналогию уравнений соответствующим уравнениям для электрических явлений,

Закон Ома для теплового потока

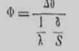
(6.53)

Закон Ома для однородного проводника

(6.54)

Тепловое сопротивление стенки

(6.55)

Видно, что между явлениями электрического тока в проводниках и явлениями теплового потока существует далеко идущая аналогия, которой часто пользуются для упрощения решения различных задач по теплопередаче. В частности, для решения задач по нагреву электрических машин и аппаратов весьма удобным оказывается применение понятия о сопротивлении тепловому потоку.

Режимы нагрева электрических аппаратов

Кратковременный и повторно-кратковременный режимы нагрева

Температура аппарата или отдельных его частей в процессе нагрева (или охлаждения) определяется отношением времени нагрева к постоянной времени нагрева аппарата или отдельной его части.

Уравнение процесса нагрева при отдаче тепла в окружающую среду по закону Ньютона имеет следующий вид

(6.56)

Теоретически время достижения установившегося превышения температуры бесконечно, но если задаться точностью 2%, то при этом можно считать, что для достижения установившегося превышения температуры время нагрева должно быть больше, чем AT,так как

Если время нагрева t<4T, то, очевидно, температура аппарата не достигнет установившегося значения.

Аналогично при охлаждении аппарата, если время охлаждения аппарата (ток через аппарат не протекает) больше 4T, то можно считать, что за такой промежуток времени температура аппарата станет равной температуре окружающей среды.

Часто встречаются такие режимы работы аппаратуры, когда время, в течение которого аппарат включен (время нагрева) меньше, чем время, необходимое для нагрева до установившейся температуры, т. е.                      , а время паузы t- (когда ток через аппарат не протекает) много больше, т. е.

Подобный режим работы аппарата называется кратковременным.

Очевидно, что при кратковременном режиме работы допустимая величина тока может быть принята большей, чем при длительном режиме.

Пусть известны допустимое превышение температуры аппарата ТДОП, длительно допустимый ток Iдл.доп или длительно допустимая мощность потерь PДЛ.ДОП и постоянная времени нагрева аппарата Т. Пусть через аппарат в кратковременном режиме за время Ткр протекает некоторый ток Iкр. Току Iкр соответствует мощность потерь Ркр. Если бы ток Iкр протекал достаточно долго, то в соответствии с уравнением (6.56) превышение температуры аппарата установилось бы равным (рис.6.8):

 

(6.57)

При времени протекания tкр максимальное превышение температуры окажется равным

(6.58)

В качестве условия мы примем, что это максимальное превышение температуры в кратковременном режиме не должно превзойти установившегося значения в длительном режиме, т. е.

 

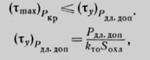
(6.59)

то, подставляя , получим

(6.60)

Откуда коэффициент допустимой перегрузки по мощности в кратковременном режиме

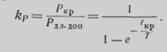
Если принять в простейшем случае, что мощность потерь пропорциональна квадрату тока, то коэффициент перегрузки по току в кратковременном режиме

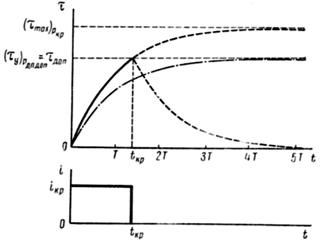
Рис.6.8. Кратковременный процесс нагрева

При конструировании аппаратов, специально предназначенных для кратковременного режима работы, надо стремиться к увеличению его постоянной времени нагрева Т, так как при этом растет коэффициент перегрузки по току и по мощности. Увеличение постоянной времени Т, как правило, достигается увеличением теплоемкости аппарата.

Если время бестоковой паузы недостаточно для полного остывания аппарата, т.е. если                     то при последующем включении аппарата его нагрев начнется при некотором значении температуры, отличающимся от температуры окружающей среды

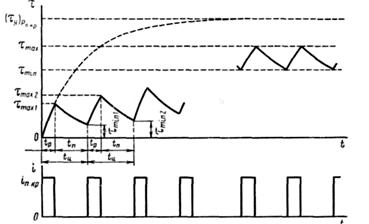
Рис.6.9.Повторно-кратковременный процесс нагрева

Существует ряд аппаратов, предназначенных для работы в повторно-кратковременном режиме. В этом режиме циклы нагрева и охлаждения аппарата строго чередуются. Обозначим время работы аппарата в одном цикле (время протекания тока) tр, а время бестоковой паузы tп. Пусть графически зависимость тока от времени в повторно-кратковременном режиме представлена на рис.6.9. Сумму назовем временем цикла tц.

В течение первого цикла за время tр1 аппарат нагревается до некоторого превышения температуры , а за время первой паузы tп1 произойдет его охлаждение до . Во втором цикле нагрев аппарата начнется при=  и за время tр2 будет достигнуто превышение температуры , но так как то >. За время второй паузы tn2 аппарат охладится и в конце второго цикла опять будет иметь место превышение температуры, которое будет больше, чем . Если такие циклы будут периодически повторяться достаточно долго, то в конце концов установится процесс колебания температуры аппарата, так называемый квазиустановившийся режим.

Если в повторно-кратковременном режиме мощность потерь в аппарате в промежутки tр равна Рп.кр, то, очевидно, максимальное превышение температуры в квазиустановившемся режиме будет ниже, чем если бы мощность Рп.кр выделялась бесконечно долго, т.е.

Для полного использования материалов в аппарате и для обеспечения надежности его работы должно соблюдаться условие

(6.61)

Рассмотрим п-й цикл при достаточно большом значении числа п квазиустановившегося режима. Для этого цикла справедливы равенства

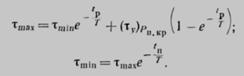
Подставив, будем иметь

(6.62)

Установившееся превышение температуры при длительном процессе выделения мощности

 

(6.63)

получим

(6.64)

тогда коэффициент перегрузки по мощности в повторно-кратковременном режиме

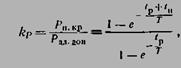
(6.65)

а коэффициент перегрузки по току

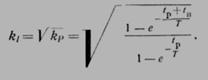
(6.66)

При расчетах аппаратов, предназначенных для повторно-кратковременного режима работы, часто используется величина относительной продолжительности включения ПВ%. Она является выраженным в процентах отношением времени работы ко времени всего цикла, т. е.

(6.67)

Для аппаратов, предназначенных к работе в повторно-кратковременном режиме, обычно задается частота включения в час п. Тогда время цикла и время работы аппарата могут быть записаны в виде

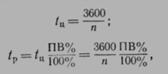
(6.68)

где п — заданная частота включений в час.

получим выражение коэффициента перегрузки по току

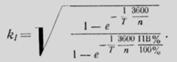
(6.69)

Процесс нагрева при коротком замыкании. Понятие 0 термической устойчивости

Режим короткого замыкания в цепи большей частью является аварийным и его обычно ликвидируют за малые промежутки времени — секунды и доли секунды, однако, как ни мала длительность протекания токов короткого замыкания, их воздействие может оказаться катастрофическим.

Обычно время воздействия токов к. з. tK 3 значительно меньше постоянной времени нагрева токоведущих частей. Легко показать, что при

      процесс нагрева происходит так, что тепло не отдается в окружающую среду. Такой процесс нагрева называют адиабатическим.

Действительно, если функцию       разложить в ряд Маклорена, то выражение примет вид

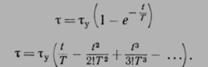
(6.70)

Так как температуры проводников в конце процесса короткого замыкания строго ограничены, каждый аппарат может быть охарактеризован допустимой величиной произведения Обычно задается не сама величина а величина тока неизменной силы, тепловое действие которого аппарат может выдержать в течение заданного времени так, что это не препятствует его дальнейшей нормальной работе. Эта величина тока называется током термической устойчивости. Чаще всего задается ток десяти-, пяти- или односекундиой термической устойчивости. Если необходимо найти ток термической устойчивости при времени действия t, отличающемся от 10 сек (или 5 сек соответственно), то это может быть легко сделано из условия

 

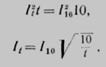
Лекция №7

Тема лекции:

Электроконтакты, понятия и теория. Конструкция и выбор коммутирующих контактов

Назначение и классификация электрических контактов

Любая электротехническая установка состоит из элементов, так или иначе связанных между собой. Соединение проводящих звеньев электрической цепи, обеспечивающее протекание электрического тока при наличии источника э. д. с, осуществляется с помощью электрических контактов.

Слово контакт от латинского слова contactus — прикосновение. Под электрическим контактом весьма часто понимается совокупность двух или нескольких проводников электрического тока, соединенных между собой и сжатых с определенной силой.

ГОСТ 2774—44 определяет электрический контакт, как «место перехода тока из одной токоведущей части в другую».

По своему назначению электрические контакты можно разделить на две группы.

1.  Соединительные контакты, которые служат только для соединения различных звеньев электрической цепи, т. е. для обеспечения протекания тока от одного звена к другому. Соединительные контакты всегда замкнуты.

2.  Коммутирующие контакты, предназначенные для включения, отключения и переключения электрических цепей.

Соединительные контакты, применяемые в токопроводах электрических аппаратов, весьма разнообразны. Некоторые типичные конструкции их изображены на рис. 3.1.

Основным требованием, предъявляемым к соединительным контактам, является надежность в длительной эксплуатации: соединительные контакты должны длительно, в пределах срока службы всей установки в целом и без повреждений допускать протекание токов нормального режима и кратковременных токов аварийных режимов работы.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25