Курсовая работа: Статистическое изучение объема, состава и динамики доходов и расходов государственного бюджета

Из табл.2 складываем все значения доходов бюджета, входящие в первый интервал, полученные значения вносим в табл.2.2, ячейку всего.

Пример: 0,7+0,5+1,2+0,9+0,8=4,1 (I)

Аналогично рассчитываем все значения расходов бюджета.

Для нахождения значения в ячейки доходы бюджета, в среднем, полученные значения ячейки всего делим на кол-во областей.

Пример: 4,1/5=1,85

Аналогично рассчитываем значения для расходов бюджета.

Вывод: В аналитической группировки с ростом доходов бюджета субъектов РФ наблюдается увеличение расходов бюджетных средств, т.е. прямая, достаточно-тесная взаимосвязь.

Сгруппируем имеющиеся признаки на группы (расчеты производим по табл.1, расходы бюджета)

R=Xmax - Xmin

R=8,7 – 1.7=7

I=R/n=7/5=1,4

Формируем интервалы:

Таблица 2.3

№ группы	Группы субъектов РФ по уровню доходов бюджета, млн. руб.	Число областей группы
1	1,9 – 3,4	3
2	3,4 – 4,9	4
3	4,9 – 6,4	8
4	6,4 – 7,9	6
5	7,9 – 9,4	9
Итого		30

2. Корреляционно-регрессионный анализ

Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению причинных связей и оценки факторов, оказывающих наибольшее влияние на результативный признак.

Построим корреляционную таблицу:

Расходы бюджета	Доходы бюджета
Группы по расходам	0,5 – 2,0	2,0 – 3,5	3,5 – 5,0	5,0 – 6,5	6,5 – 8
1,9 – 3,4	****	********
3,4 – 4,9			************
4,9 – 6,4
6,4 – 7,9				**	**
7,9 - более					**

Вывод: наличие достаточно тесной взаимосвязи между признаками доходов бюджета и расходов бюджета.

Задание 3

По результатам выполнения задания 1 с вероятностью 0,683 определите:

1.  Ошибку выборки среднего дохода бюджета и границы, в которых он будет находиться в генеральной совокупности.

2.  Ошибку выборки доли регионов со средним доходом бюджета 5 млрд. руб. и более и границы, в которых будет находиться генеральная доля.

Решение.

Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

для средней ;                  ;              (2.10)

для доли  ;                       .            (2.11)

Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от  до .

Аналогичным образом может быть записан доверительный интервал генеральной доли:  ; .

1. При механическом отборе предельная ошибка выборки для средней определяется по формуле:

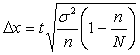,                                     (2.12)

Где t ─ нормированное отклонение ─ «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;  – генеральная дисперсия (дисперсия признака в генеральной совокупности) – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической;  – относительное число единиц.

Рассчитаем предельную ошибку по формуле (2.12):

 или 25% (по условию);

По данным Ф(t) для вероятности 0,683 находим t = 1 (см. табл. 2.4)

Таблица 2.4

Удвоенная нормированная функция Лапласа

t	1,00	1,96	2,00	2,58	3,00
ф(t)	0,683	0,95	0,954	0,99	0,997

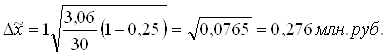
оверительный интервал (пределы) генеральной средней исчисляем, исходя из двойного неравенства (2.10):

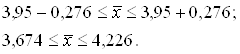
Таким образом, с вероятностью 0,683 можно утверждать, что средний доход бюджета регионов, в генеральной совокупности, колеблется в пределах от 3,621 до 4,179.

2.  Предельную ошибку доли определяем по формуле бесповторного отбора (механическая выборка всегда является бесповторной):

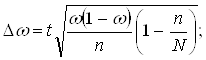 (2.13)

Число регионов со среднем доходом бюджета 5 млрд. руб. и более равно 7, т.е. m = 7, а        .

Находим предельную ошибку доли по формуле (2.13):

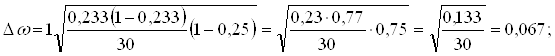
Доверительные пределы генеральной доли исчисляем, исходя из двойного неравенства (2.11):

0,1660,3

Таким образом, с вероятностью 0,683 можно утверждать, что доля регионов со среднем доходом бюджета 5 млрд. руб. и более колеблется от 16,6 до 30%.

Задание 4

Исполнение регионального бюджета в процентах к валовому региональному продукту (ВРП) характеризуется следующими данными:

Таблица 2.5

Месяц	Налоговые поступления
	2002 г.	2003 г.	2004 г.
Январь	2,5	2,6	2,4
Февраль	2,6	2,7	2,3
Март	3	2,8	2,5
Апрель	2,9	2,8	2,1
Май	2,8	2,7	2,3
Июнь	2,7	2,8	2,2
Июль	2,9	2,7	2,6
Август	2,8	2,7	2,6
Сентябрь	2,9	2,8	2,7
Октябрь	3	2,9	2,8
Ноябрь	3,1	3	3
Декабрь	3,2	2,9	3,3

ВРП в 2002 г. Составил 26 млрд. руб., а в 2003 и 2004 гг. соответственно 29,1 млрд. и 32,2 млрд. руб.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9