Курсовая работа: Статистическое изучение объема, состава и динамики доходов и расходов государственного бюджета

Признак ─ доходы бюджета.

Число групп ─ пять.

Решение.

Статистическая группировка в зависимости от решаемых задач подразделяются на типологические, структурные, аналитические. Статистическая группировка позволяет дать характеристику размеров, структуры и взаимосвязи изучаемых явлений, выявить их закономерности.

Важным направлением в статистической сводке является построение рядов распределения, одно из назначений которых состоит в изучении структуры исследуемой совокупности, характера и закономерности распределения.

Ряд распределения – это простейшая группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака.

1. Признак – это доходы бюджета (х).

Построим ранжированный ряд. Для этого найдем i.

Величина равного интервала рассчитывается по формуле:

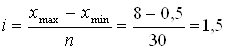,     (2.1)

где – число выделенных интервалов.

Таким образом распределение по группам:

1 группа: 0,5-2,0

2 группа: 2-3,5,0

3 группа: 3,5-5,0

4 группа: 5-6,5,0

5 группа: 6,5-8,0

Заполним таблицу по группам.

Таблица 2.1

Распределение регионов по доходам бюджета

№ группы	Группы субъектов РФ по уровню доходов бюджета, млн. руб.	Число областей группы
1	0,5-2,0	5
2	2-3,5,0	6
3	3,5-5,0	12
4	5-6,5,0	4
5	6,5-8,0	3
Итого		30

Т.о. интервальный ряд распределения показал, что наибольшее количество субъектов РФ имеют уровень доходов от 3,5-5 млн. руб.

2. Построим график полученного ряда распределения и графически изобразим на нем моду:

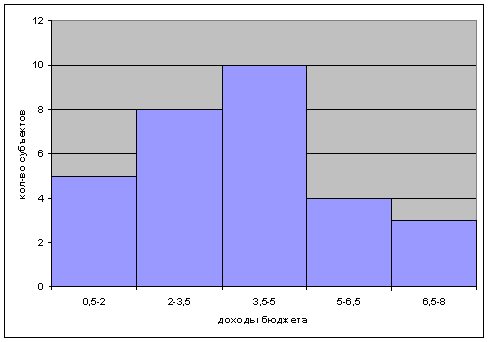
Рис. 2.1. График ряда распределения.

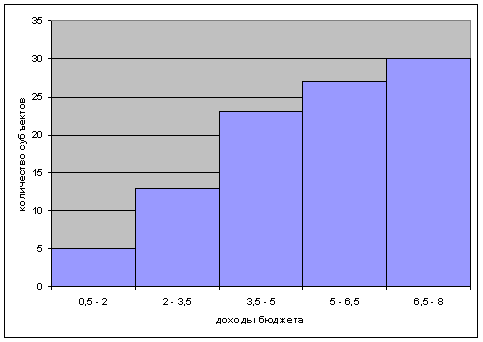
Для графического изображения медианы построим комуляты и рассчитаем комулятивные частоты таблицы.

Таблица 2.2

1	5	5
2	8 (5+8)	13
3	10 (5+8+10)	23
4	4 (5+8+10+4)	27
5	3 (5+8+10+4+3)	30

Рассчитаем показатели: моду и медиану.

Мода - наиболее часто встречающееся значение признака. В интервальном ряду определяется модальный интервал (имеет наибольшую частоту). Значение моды определяется по формуле:

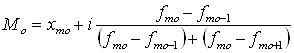       ,        (2.2)

  - нижняя граница модального интервала,

  - частота модального интервала,

        - частота интервала, предшествующего модальному,

        - частота интервала, следующего за модальным.

Модальный интервал – третий (3,5-5), т.к. он имеет наибольшую частоту (10).

Найдем моду по формуле (2.2):

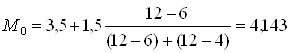
Итак, модальным значением доходов бюджета регионов являются доходы, равные 3,875 млн. руб.

Медиана Ме − это вариант, который находится в середине вариационного ряда. Чтобы найти медиану необходимо отыскать значение признака, которое находится в середине упорядоченного ряда.

Медианным является интервал, в котором сумма накопленных частностей превысит половину общего числа наблюдений, т.е. 15.

Значение медианы вычисляется по формуле:

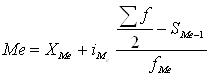 ,                                                           (2.3)

где −  - нижняя граница медианного интервала,

            - накопленная частота интервала, предшествующего медианному,

 - величина интервала,

 - частота медианного интервала.

 - половина от общего числа наблюдений

Найдем медианный интервал. Таким интервалом будет интервал доходов бюджета регионов (3,5-5 млн. руб.), поскольку его накопленная частота равна 23 (10+8+5), что превышает половину суммы всех частот (30:2=15). Нижняя граница интервала 3,5 млн. руб.. его частота 10; частота накопленная до него, равна 11.

Подставив данные в формулу (2.3), получим, млн. руб.:

.

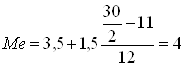Полученный результат говорит о том, что из 30 регионов 15 регионов имеют доходы бюджета менее 3 млн. руб., а 15 регионов − более.

3. Рассчитываем характеристику ряда распределения регионов. Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака () объединены в группы, имеющие различное число единиц (), называемое частотой (весом), применяется средняя арифметическая взвешенная:

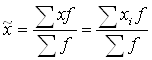                                                                (2.4)

где вес (частота повторения одинаковых признаков);

сумма произведений величины признаков на их частоты;

общая численность единиц совокупности;

i – номер группы

1 (0,5+2,0)/2=1,25

2 (2,0+3,5)/2=2,75

3 (3,5+5,0)/2=4,25

4 (5,0+6,5)/2=5,75

5 (6,5+8)/2=7,25

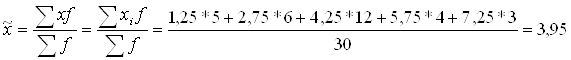 (2.4)        

Таблица 2.1

(хi-х2)	(хi-х2)*f	∑(хi-х2)*f
(1,25-3,95)2	7,29*5=36,45	36,45+8,64+1,08+12,96+32,67= 91,8
(2,75-3,95)2	1,44*6=8,64
(4,25-3,95)2	0,09*12=1,08
(5,75-3,95)2	3,24*4=12,96
(7,25-3,95)2	10,89*3=32,67

Среднее квадратическое отклонение () представляет собой корень квадратный из дисперсии и равно:

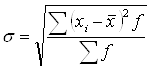- взвешенная. (2.5)

.

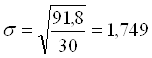Среднеквадратическое отклонение показывает, что значение признака в совокупности отклоняется от средней величины в ту или иную сторону в среднем на 1,772 млн. руб.

Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения и средней арифметической:

 (2.6)

По величине коэффициента вариации можно судить о степени вариации признаков, а, следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.

Вычислим коэффициент вариации по формуле (2.6):

.

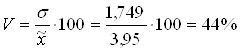Если коэффициент вариации выше 40%, значит вариация сильная, средняя величина плохо представляет всю совокупность, является нетипичной, ненадежной.

Задание 2

Связь между признаками – доходы и расходы бюджета.

Установить связь между признаками.

1. Аналитическая группировка позволяет изучать взаимосвязь факторного и результативно признаков.

Основные этапы проведения аналитической группировки – обоснование и выбор факторного и результативного признаков, подсчет числа единиц в в пределах созданных групп, а также исчисление средних размеров результативного показателя. Результаты группировки оформляют в таблице 2.2

Таблица 2.2

Группировка регионов по доходам бюджета

Интервалы	Кол-во областей	Доходы бюджета, млн.руб.		Расходы бюджета, млн.руб.
		Всего	В среднем	Всего	В среднем
0,5 – 2,0	5	4,1	0,82	5,4	1,8
2,0 – 3,5	6	13,5	2,25	11,4	2,85
3,5 – 5,0	12	48	4	35,2	4,4
5,0 – 6,5	4	23,2	5,8	33,6	5,6
6,5 – 8,0	3	23,1	7,7	68,9	7,65
∑	30	111,9 ∑30	0,686 ∑30/30	154,5 ∑30	0,743 ∑30/30

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9