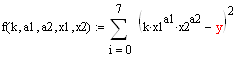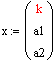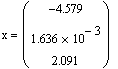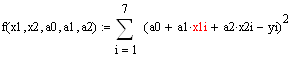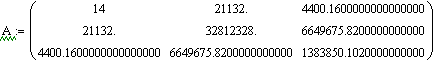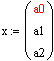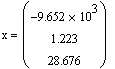Курсовая работа: Комплексный анализ рыбной отрасли

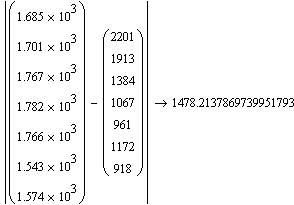
1. ПФ Кобба – Дугласа.

2. Линейная ПФ.

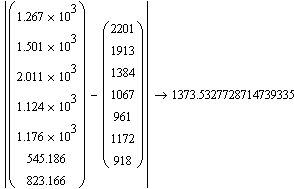
Следовательно, вычисление отклонения дает нам следующие результаты: линейная производственная функция F(K,L)=-9652+1,223K+28,676L лучше идентифицирует производственный процесс выпуска рыбной продукции за указанный период.

2.3. Построение статистической модели Леонтьева

Эффективное ведение народного хозяйства предполагает наличие баланса между отдельными отраслями. Каждая от­расль при этом выступает двояко: с одной стороны, как про­изводитель некоторой продукции, а с другой — как потреби­тель продуктов, вырабатываемых другими отраслями.

Предположим, что вся производящая сфера народного хозяйства разбита на некоторое число n отраслей, каждая из которых производит свой однородный продукт, причем раз­ные отрасли производят разные продукты. Разумеется, та­кое представление об отрасли является в значительной мере абстракцией, так как в реальной экономике отрасль опреде­ляется не только названием выпускаемого продукта, но и ве­домственной принадлежностью своих предприятий (например, данному министерству, тресту и т. п.). Однако представление об отрасли в указанном выше смысле (как "чистой" отрасли) все же полезно, так как оно позволяет провести анализ сло­жившейся технологической структуры народного хозяйства, изучить функционирование народного хозяйства "в первом приближении".

Итак, предполагаем, что имеется n различных отраслей; О1, …,Оn, каждая из которых производит свой продукт. В дальнейшем отрасль Оi будем коротко называть "i-я отрасль". В процессе производства своего продукта каждая отрасль нуж­дается в продукции других отраслей (производственное по­требление). Будем вести речь о некотором определенном про­межутке времени [Т0, Т1] (обычно таким промежутком служит плановый год) и введем следующие обозначения:

xi — общий объем продукции отрасли i за данный проме­жуток времени — так называемый валовой выпуск отрасли г;

xij — объем продукции отрасли i, расходуемый отраслью j в процессе производства;

yi — объем продукции отрасли i, предназначенный к по­треблению в непроизводственной сфере, — объем конечного потребления.

Этот объем составляет обычно более 75% всей произве­денной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление, обеспечение общественных по­требностей (просвещение, наука, здравоохранение и т. д.), по­ставки на экспорт.

Указанные величины можно свести в таблицу. Обратим наше внимание на элементы (xij ). Отрасль пред­ставлена двояким образом. Как элемент строки она выступа­ет в роли поставщика производимой ею продукции, а как эле­мент столбца — в роли потребителя продукции других отрас­лей экономической системы.

Производственное потребление	Конечное потребление	Валовой выпуск
x11 x12 x13….. x1n	y1	x1
x11 x12 x13….. x1n	y2	x2
x11 x12 x13….. x1n	yn	x3

Балансовый характер этой таблицы выражается в том, что при любом i =1,...,п должно выполняться соотношение:

хi= xi1 + xi2  +  xi3 + xin  +  уi ,           (4.1)                                                                                                                                                                                                                                                                                

означающее, что валовой выпуск хi расходуется на произ­водственное потребление, равное xi1 + xi2  +  xi3 + xin  и непроиз­водственное потребление, равное уi Будем называть (4.1) соотношениями баланса. Таким образом, таблица отражает ба­ланс между производством и потреблением.

Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки...), или стоимо­стными.

Леонтьев, рассматривая развитие экономики, обратил внимание на важное обстоятельство. Величины  остаются постоянными в течение ряда лет. Это обусловливается примерным постоянством используемой технологии.

Таким образом, сделаем такое допущение: для выпуска любого объема хj продукции j необходимо затратить продук­цию отрасли i в количестве ,  где  — постоянный коэф­фициент. Проще говоря, материальные издержки пропорцио­нальны объему производимой продукции. Это допущение по­стулирует линейность существующей технологии. Принцип ли­нейности распространяется и на другие виды издержек, на­пример, на оплату труда, а также на нормативную прибыль.

Итак, согласно гипотезе линейности имеем:

          (4.2)

Коэффициенты ац называют коэффициентами прямых затрат (коэффициенты материалоемкости).

В предположении линейности соотношения (4.1) прини­мают вид:

х1= а11х1 + а12х2 + ... + а1пхп + у1 ,

х1= а21х1 + а22х2 + ... + а2пхп + у2 ,

………

хn= аn1х1 + аn2х2 + ... + аnпхп + уn .

или в матричной записи:

,

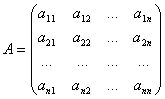
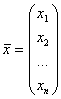
где   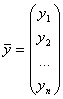                      (4.3)

Вектор  называется вектором валового выпуска, вектор у называется вектором конечного потребления, а матрица А — матрицей прямых затрат. Соотношение (4.3) называется урав­нением линейного межотраслевого баланса. Вместе с изложен­ной интерпретацией матрицы А и векторов  и  это соот­ношение называют также моделью Леонтьева.

Уравнения межотраслевого баланса можно использовать для целей планирования. В этом случае задача ставится так: для предстоящего планового периода [Т0, Т1] задается вектор  конечного потребления. Требуется определить вектор  валового выпуска. Проще говоря, нужно решить задачу: сколь­ко следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В этом случае необходимо решить систему линейных уравнений (4.3) с неизвестным вектором  при заданной матрице А и векто­ре . При этом нужно иметь в виду следующие особенности системы (4.3):

1)  Все компоненты матрицы А и вектора    неотрица­тельны (это вытекает из экономического смысла А и вектора у и записывается так: А  0,   0.

2)  Все компоненты вектора  также должны быть нео­трицательными:   0.

Замечание: Обратим внимание на смысл коэффициентов а у прямых затрат в случае стоимостного (а не натурального) баланса. В этом случае из (4.2) видно, что аij совпадает со значением xij при xi =1(1 руб. ). Таким образом, аij есть стоимость продукции отрасли i, вложенной в 1 руб. продукции j. Отсюда видно, что стоимостный подход по сравнению с натуральным обладает более широкими возможностями.

В стоимостном выражении первоначальная таблица выглядит следующим образом.

Производство продукции, B	Потребление продукции					Конечная продукция Y	Валовой выпуск
	Рыбная	Логистика	Судоремонтная	Пищевая	Машино и приборо-строение
Рыбная	452,64	6789,6	33042,72	4526,4	452,64	56700	101964
Логистика	5915,76	29578,8	14789,4	44368,2	53241,84	56430	204324
Судоремонтная	35239,8	1174,66	70479,6	5873,3	4698,64	390860	508326
Пищевая	250932	5018,64	50186,4	150559,2	45167,76	787890	1289754
Машино и приборо-строение	82186,6	82186,6	41093,3	82186,6	123279,9	323630	734563

Преобразуем таблицу, найдя коэффициенты a - коэффициенты прямых затрат

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13