Курсовая работа: Комплексный анализ рыбной отрасли

Про учет инфляции можно сказать следующее. На основные производственные фонды она не повлияет в силу их физического выражения. На спрос потребителей инфляция, конечно, повлияет (потребление рыбы будет повышаться как предмета первой необходимости, а еще вследствие снижения уровня жизни, ухудшения здоровья). Но это уже аспект не только экономики, но и других сфер деятельности человека, поэтому сказать что-то определенное относительно изменения объема спроса сложно. А вот изменение выпуска вполне предсказуемо. Спрос порождает предложение, следовательно, так при инфляции деньги обесцениваются, спрос повысится, что вызовет снижение объема предложения при более высокой цене. Еще, конечно, необходимо учесть повышение цен на ресурсы производства для производителя. Упрощая схему, можно предположить, что реальный объем предложения будет равен в момент времени t: , где i – годовой рост инфляции. Тогда таблица измененных объемов выпусков будет выглядеть следующим образом по годам:

Отрасль	x при t=1	x при t=2	x при t=3	x при t=4	x при t=5	x при t=6
Рыбная	137821,51	90735,98	63657,45	52173,46	57902,22	137821,51
Логистика	392426,65	355978,65	362658,68	335593,26	434097,43	392426,65
Судоремонтная	296000,20	291598,07	272025,21	282447,56	237135,95	296000,20
Пищевая	403250,75	375866,90	369337,88	302166,97	281985,13	403250,75
Машино и приборо-строение	477435,26	436090,78	407872,90	310504,67	303564,16	477435,26

2.6. Построение магистральной модели

Модели межотраслевого баланса Леонтьева позволяют планировать траекторию функционирования производственного сектора экономики. Так, в рамках динамической модели Леонтьева синхронно с траекторией валовых выпусков строятся сопутствующие траектории основных производственных фондов и конечных спросов .

С научной и практической точки зрения важно существование в рамках модели сбалансированной траектории, такой, что

при t = 0, 1, 2, ...

λ - const, λ > 1.

При этом траектории и , сопутствующие сбалансированной траектории, тоже являются сбалансированными и обладают тем же темпом роста λ, то есть

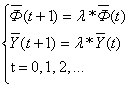
Возникают два вопроса:

1) Существует ли в СММБ и ДММБ сбалансированная траектория , темп роста λ, которой максимален?

2) Если ответ на первый вопрос положителен, то чем траектория лучше любой другой «хорошей» (в некотором смысле) траектории?

Ответ на первый вопрос применительно к ДММБ несложно дать тотчас: константа λ в сбалансированной траектории единственна (это следует из методики ее определения, а поэтому траектория является сбалансированной траекторией с максимальным темпом роста λ. Уравнение элементов этой траектории выглядит так:

Сложнее обстоит дело с ответом на второй вопрос, поскольку этот ответ базируется на специальной теории, развитой в рамках математической экономики для исследования производственного сектора при помощи общих теоретико-аналитических моделей «затраты-выпуск». Знакомство с важнейшими понятиями и моделями этой теории составляет содержание данного пункта. В итоге будет получен ответ на второй вопрос в форме точного математического утверждения. Качественно же суть этого утверждения такова: при определенных условиях любая «хорошая» (в некотором смысле) траектория

экономики лишь только на начальном и конечном временном интервале, возможно, отклоняется от магистрали . Именно данное свойство магистралей обусловливает интерес к тем моделям «затраты-выпуск», в которых магистрали существуют. Модели «затраты-выпуск», в которых существуют магистрали, принято называть магистральными.

Первую магистральную модель построил в 30-х годах 20-го века выдающийся американский математик Дж. фон Нейман. Эта модель, которую называют моделью расширяющейся экономики фон Неймана, отказала глубокое воздействие на математическую экономику. Подчеркнем, что СММБ Леонтьева суть частный случай модели фон Неймана.

При обсуждении модели потребуется формализация понятий производства и производственного процесса.

Под производством понимается преобразование конкретных количеств затрачиваемых продуктов в некоторые конкретные количества выпускаемых продуктов. Такое преобразование осуществляется при помощи заданной технологии Т. Технологическим (или производственным) процессом называется пара (, ), состоящая из конкретного вектора затрат и конкретного вектора выпусков.

Рассмотрим некоторый технологический процесс (ТП) (, ). Чтобы подчеркнуть, что его компоненты и связаны технологией Т, будем, при необходимости, обозначать ТП еще и так: (Т).

Пусть Т - какая-то заданная технология. В общем случае она позволяет реализовать некоторое множество М конкретных и различных ТП, как-то: (, ), (, ), ... Все эти ТП, собранные в множество М, принято именовать технологическим множеством (ТМ) производственного сектора экономики. Так что

Модель Гейла

Моделью Гейла называется ТМ, элементы которого удовлетворяют 4-м условиям, как то:

1. Если , то =0 . Это естественное свойство принято называть неосуществимостью «рога изобилия».

2. М представляет собой выпуклый конус в .

3. Для каждого номера i=1,2, ..., n, где n — количество компонент векторов и , существует ТП такой, что компонента вектора положительна. Другими словами, свойство 3 означает, что каждый из n продуктов может быть произведен, так что невоспроизводимые ресурсы продуктами в модели Гейла не являются.

4. Множество М замкнуто в . Это свойство, означающее, что множество М содержит все свои предельные точки, имеет сугубо математическую подоплеку, доставляющую удобство в аналитических исследованиях.

Пусть М — модель Гейла. В рамках модели М естественно задается динамика развития экономики. Пусть ; будем полагать, что вектор потребляется (в процессе производства) в текущий момент времени t, а вектор производится в следующий момент (t+1). Тогда характеризует состояние экономики (в смысле запаса продуктов) в текущий момент t. Аналогично, вектор характеризует состояние экономики в следующий момент (t + 1), причем пара . Далее, вектор будет потребляться в момент (t + 1), а в момент (t + 2) окажется произведенным вектор и т.д. Таким образом, осуществляется динамическое движение экономики

Это движение самоподдерживающееся, поскольку какой-либо приток извне, полагаем, отсутствует.

Последовательность называется допустимой траекторией в модели Гейла М на конечном интервале времени Т, если при t = 0, 1, 2, ..., T-1 справедливо отношение . Если Т бесконечно, то траектория допустима на бесконечном интервале времени. Не равная тождественно нулю допустимая траектория называется траекторией сбалансированного роста, если при t = 0, 1, 2,... справедливо равенство

в котором λ - положительная константа, темп роста сбалансированной траектории. Сбалансированная траектория называется магистралью, если ее темп роста λ максимален.

Как следует из данного определения, магистраль, если она существует, принадлежит при всех t = 0, 1,2,... лучу

Этот луч принято называть неймановским лучом.

Понятие темпа роста определено выражением применительно к сбалансированным траекториям модели Гейла.

Рассмотрим сначала специальное подмножество МоМ тривиальных ТП модели Гейла, то есть таких процессов , у которых . Можно показать (см. задачу 18 в конце гл. 9), пользуясь определением модели Гейла, что подмножество Мо состоит из одного элемента (,). Его темп роста определяем следующим образом

λ(,) = 0.

Пусть теперь - любой нетривиальный ТП; его темп роста определяется так:

В правой части последнего равенства минимум берется по всем положительным компонентам вектора .

Рассмотрим 2 последних выражения (9.6.16)-(9.6.17), задающих определение темпа роста любого ТП , или говоря иначе, определяющие на множестве М скалярную неотрицательную функцию . Каковы свойства этой функции? Отметим три из них.