 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Дипломная работа: Моделирование нагрева асинхронного двигателя
где RΔc – тепловое сопротивление стыка сердечник станина, 0С / Вт;
Rсп – тепловое сопротивление спинки сердечника (2.41), 0С / Вт.
Тепловое сопротивление стыка сердечник станина:
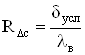 , (2.52)
, (2.52)
где δусл – условный зазор в стыке сердечник станина, м.
Для двигателей серии 4А величина условного зазора приблизительно равна:
δусл≈(20∙Da+26) ∙10-6. (2.53)
7) Тепловое сопротивление между внутренним воздухом и корпусом
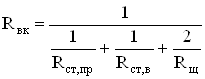 , (2.54)
, (2.54)
где Rст,пр – тепловое сопротивление между внутренней поверхностью станины со стороны привода и внутренним воздухом, 0С / Вт;
Rст,в-тепловое сопротивление между внутренней поверхностью станины со стороны вентилятора и внутренним воздухом, 0С / Вт;
Rщ – тепловое сопротивление между внутренней поверхностью подшипникового щита и внутренним воздухом, 0С / Вт.
Тепловое сопротивление между внутренней поверхностью станины со стороны привода и внутренним воздухом:
 , (2.55)
, (2.55)
где Fст,пр – площадь внутренней поверхности свеса станины со стороны привода, м2;
αс – коэффициент теплоотдачи внутренней поверхности свесов станины, Вт/(м2∙0С).
Площадь внутренней поверхности свеса со стороны привода:
![]() , (2.56)
, (2.56)
где lсв,пр – длина свеса станины со стороны привода, м.
Коэффициент теплоотдачи внутренней поверхности свесов станины:
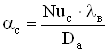 , (2.57)
, (2.57)
где Nuc – число Нуссельта для внутренней поверхности свесов станины.
Число Нуссельта для внутренней поверхности свесов станины зависит от высоты оси вращения и от наличия диффузора в полости лобовых частей.
Для высоты оси вращения h<160 мм:
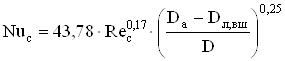 , (2.58)
, (2.58)
для высоты оси вращения h=160–250 мм:
без
диффузора- ![]() ; (2.59)
; (2.59)
с диффузором-
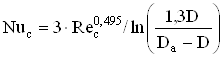 , (2.60)
, (2.60)
где Rec – число Рейнольдса для внутренней поверхности свесов станины;
D – внутренний диаметр сердечника статора, м.
Число Рейнольдса для внутренней поверхности свесов станины:
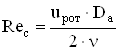 . (2.61)
. (2.61)
Тепловое сопротивление между внутренней поверхностью станины со стороны вентилятора и внутренним воздухом:
 , (2.62)
, (2.62)
где Fст,в- площадь внутренней поверхности свеса со стороны вентилятора, м2;
αс – коэффициент теплоотдачи внутренней поверхности свесов станины, Вт/(м2∙0С).
Площадь внутренней поверхности свеса со стороны вентилятора:
![]() , (2.63)
, (2.63)
где lсв,в- длина свеса станины со стороны вентилятора, м.
Тепловое сопротивление между внутренней поверхностью подшипникового щита и внутренним воздухом:
 , (2.64)
, (2.64)
где Fщ – площадь внутренней поверхности подшипникового щита, м2;
αщ – коэффициент теплоотдачи внутренней поверхности подшипникового щита, Вт/(м2∙0С).
Площадь внутренней поверхности подшипникового щита:
 . (2.65)
. (2.65)
Коэффициент теплоотдачи внутренней поверхности подшипникового щита:
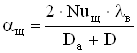 , (2.66)
, (2.66)
где Nuщ – число Нуссельта для внутренней поверхности подшипникового щита.
Число Нуссельта для внутренней поверхности подшипникового щита зависит от высоты оси вращения и от наличия диффузора в полости лобовых частей.
Для высоты оси вращения h<160 мм:
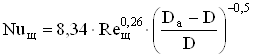 , (2.67)
, (2.67)
для высоты оси вращения h=160–250 мм:
без
диффузора- 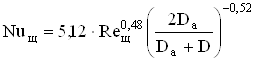 ; (2.68)
; (2.68)
с диффузором-
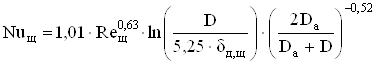 , (2.69)
, (2.69)
где Reщ – число Рейнольдса для внутренней поверхности свесов станины;
δд,щ – зазор между диффузором и щитом в месте крепления, м.
Число Рейнольдса для внутренней поверхности подшипниковых щитов:
 . (2.70)
. (2.70)
8) Тепловое сопротивление между внешним воздухом и корпусом
 , (2.71)
, (2.71)
где Rвс,пр – тепловое сопротивление между наружной поверхностью свисающей части станины со стороны привода и внешним воздухом, 0С / Вт;
Rвс – тепловое сопротивление между наружной поверхностью станины над пакетом и внешним воздухом, 0С / Вт;
Rвс,в- тепловое сопротивление между наружной поверхностью свисающей части станины со стороны вентилятора и внешним воздухом, 0С / Вт;
Rвщ,пр – тепловое сопротивление между наружной поверхностью подшипникового щита со стороны привода и внешним воздухом, 0С / Вт;
Rвщ,в- тепловое сопротивление между наружной поверхностью подшипникового щита со стороны вентилятора и внешним воздухом, 0С / Вт.
Тепловое сопротивление между наружной поверхностью станины над пакетом и внешним воздухом:
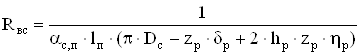 , (2.72)
, (2.72)
где αс,п – коэффициент теплоотдачи наружной поверхности станины над пакетом, Вт/(м2∙0С);
Dc – диаметр станины у основания ребер, м;
zp – количество ребер станины;
δр – толщина ребра станины, м;
hр – высота ребра станины, м;
ηр – коэффициент качества ребра станины.
Тепловое сопротивление между наружной поверхностью свисающей части станины со стороны привода и внешним воздухом:
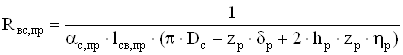 , (2.73)
, (2.73)
где αс,пр – коэффициент теплоотдачи наружной поверхности станины со стороны привода, Вт/(м2∙0С).
Тепловое сопротивление между наружной поверхностью свисающей части станины со стороны вентилятора и внешним воздухом:
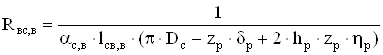 , (2.74)
, (2.74)
где αс,в- коэффициент теплоотдачи наружной поверхности станины со стороны вентилятора, Вт/(м2∙0С).
Коэффициент теплоотдачи наружной поверхности станины над пакетом:
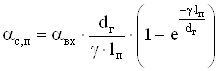 , (2.75)
, (2.75)
где αвх – коэффициент теплоотдачи на входе в межреберные каналы станины, Вт/(м2∙0С);
dг – гидравлический диаметр межреберного канала, м;
γ – коэффициент уменьшения теплоотдачи по длине станины.
Коэффициент теплоотдачи наружной поверхности станины со стороны привода:
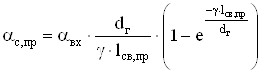 . (2.76)
. (2.76)
Коэффициент теплоотдачи наружной поверхности станины со стороны вентилятора:
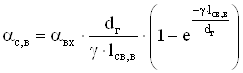 . (2.77)
. (2.77)
Гидравлический диаметр межреберного канала:
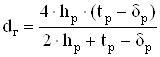 , (2.78)
, (2.78)
где tр – шаг ребер станины, м.
Коэффициент уменьшения теплоотдачи по длине станины:
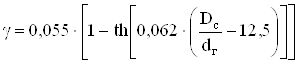 . (2.79)
. (2.79)
Коэффициент теплоотдачи на входе в межреберные каналы станины:
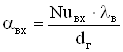 , (2.80)
, (2.80)
где Nuвх – число Нуссельта для межреберных каналов.
Число Нуссельта для межреберных каналов:
![]() , (2.81)
, (2.81)
где Reэф – число Рейнольдса для межреберных каналов.
Число Рейнольдса для межреберных каналов:
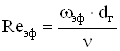 , (2.82)
, (2.82)
где ωэф – эффективная скорость на входе в межреберные каналы, м/с.
Эффективная скорость на входе в межреберные каналы:
![]() , (2.83)
, (2.83)
где ωвх≈0,45∙uвент – расходная скорость на входе в каналы, м/с;
uвент – окружная скорость вентилятора, м/с.
Коэффициент качества ребра станины:
![]() , (2.84)
, (2.84)
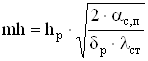 , (2.85)
, (2.85)
где λст – коэффициент теплопроводности материала станины, Вт/(м∙0С).
Тепловое сопротивление между наружной поверхностью подшипникового щита со стороны привода и внешним воздухом:
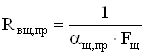 , (2.86)
, (2.86)
где αщ,пр – коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны привода, Вт/(м2∙0С).
Коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны привода:
![]() . (2.87)
. (2.87)
Тепловое сопротивление между наружной поверхностью подшипникового щита со стороны вентилятора и внешним воздухом:
 , (2.88)
, (2.88)
где αщ,в- коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны вентилятора, Вт/(м2∙0С).
Коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны вентилятора зависит от высоты оси вращения.
Для высоты оси вращения h<160 мм:
![]() , (2.89)
, (2.89)
для высоты оси вращения h>160 мм:
![]() . (2.90)
. (2.90)
Как видно, для определения тепловых сопротивлений требуется знать большое количество конструктивных параметров. Ниже приводятся полный перечень необходимых для расчета сопротивлений данных:
Паспортные данные
1. Синхронная частота вращения n1, об/мин;
2. Количество пар полюсов p.
Параметры станины
1. Высота оси вращения h, мм;
2. Диаметр станины у основания ребер Dc, м;
3. Длина свисающей части станины со стороны привода lсв.пр, м;
4. Длина свисающей части станины со стороны вентилятора lсв.в, м;
5. Зазор между диффузором и подшипниковым щитом в месте крепления δд.щ, м;
6. Количество ребер станины zp;
7. Высота ребра станины hp, м;
8. Толщина ребра станины δр, м.
Параметры вентилятора
1. Внешний диаметр вентилятора Dвент, м.
Параметры статора
1. Внешний диаметр сердечника Da, м;
2. Внутренний диаметр сердечника D, м;
3. Длина паза lп, м;
4. Число пазов статора Z1;
5. Коэффициент шихтовки (заполнения пакета сталью) kш=0,97.
Параметры паза статора
1. Большая ширина паза b1, м;
2. Меньшая ширина паза b2, м;
3. Высота паза hп, м;
4. Коэффициент заполнения паза kз;
5. Высота шлица hш;
6. Ширина шлица bш, м;
7. Высота зубца hз, м;
8. Ширина зубца bз, м.
Параметры обмотки
1. Количество витков в обмотке фазы ω1;
2. Число параллельных ветвей а;
3. Средняя длина витка обмотки lср1, м;
4. Длина вылета лобовой части обмотки с одной стороны lл.в, м;
5. Диаметр изолированного проводника dи, мм;
6. Коэффициент пропитки обмотки kп;
7. Толщина окраски обмотки в лобовой части δокр, м;
Параметры пазовой изоляции
1. Толщина пазовой изоляции δи.п, м.
Параметры ротора
1. Внешний диаметр ротора Dрот, м;
2. Число пазов ротора Z2;
3. Ширина короткозамыкающего кольца bк, м;
4. Высота короткозамыкающего кольца aк, м;
5. Ширина лопатки ротора bл, м;
6. Высота лопатки ротора ал, м;
7. Количество лопаток ротора zл;
8. Коэффициент качества лопатки, рассматриваемой как ребро ηл;
9. Толщина воздушного зазора между ротором и статором δ, м.
Общие физические величины
1. Кинематическая вязкость воздуха ν, м2/с;
2. Коэффициент теплопроводности воздуха λв, Вт/(0С∙м);
3. Средняя температура обмотки Tср, 0С;
4. Коэффициент теплопроводности меди обмотки λм, Вт/(0С∙м);
5. Коэффициент теплопроводности алюминия клетки λа, Вт/(0С∙м);
6. Коэффициент теплопроводности материала станины λст, Вт/(0С∙м);
7. Коэффициент теплопроводности стали пакета статора λс, Вт/(0С∙м);
8. Коэффициент теплопроводности пропиточного состава обмотки λп, Вт/(0С∙м);
9. Коэффициент теплопроводности изоляции проводов λи, Вт/(0С∙м);
10. Коэффициент теплопроводности окраски обмотки в лобовой части λокр, Вт/(0С∙м).
Расчет теплоемкостей меди и стали
2.3.1 Определение теплоемкости меди
Теплоемкость меди равна:
![]() , (2.91)
, (2.91)
где mм – масса меди обмотки статора, кг;
см – удельная теплоемкость меди обмотки статора, Дж/(кг∙0С).
Масса меди обмотки статора:
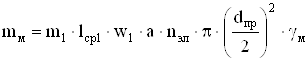 , (2.92)
, (2.92)
где m1 – число фаз обмотки статора;
lср1 – средняя длина витка обмотки статора, м;
w1 – число витков обмотки статора;
а – количество параллельных ветвей обмотки статора;
nэл – количество элементарных проводников в эффективном;
dпр – диаметр элементарного проводника, м;
γм – плотность меди обмотки, кг/м3.
Определение теплоемкости стали
![]() , (2.93)
, (2.93)
где mя – масса ярма статора, кг;
mз – масса зубцов статора, кг;
сст – удельная теплоемкость стали пакета статора, Дж/(кг∙0С).
Масса ярма статора:
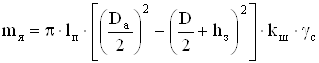 , (2.94)
, (2.94)
где γс – плотность стали пакета статора, кг/м3.
Масса зубцов статора:
![]() . (2.95)
. (2.95)
2.4.1 Потери в обмотке статора
При определении потерь в обмотке статора не учитываем увеличение активного сопротивления пазовой части обмотки статора за счет эффекта вытеснения тока.
Потери в лобовой и пазовой частях обмотки [4]:
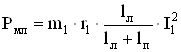 , (2.96)
, (2.96)
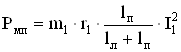 , (2.97)
, (2.97)
где r1 – активное сопротивление фазы обмотки статора, Ом;
lл – длина лобовой части обмотки с одной стороны, м;
I1 – ток фазы обмотки статора, А.
Полные потери в меди обмотки статора:
![]() . (2.98)
. (2.98)
Активное сопротивление фазы обмотки статора:
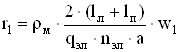 , (2.99)
, (2.99)
где ρм – удельное сопротивление меди обмотки статора при ожидаемой температуре, Ом∙м;
qэл=π(dэл/2)2 – площадь поперечного сечения элементарного проводника, м2.
Ток фазы обмотки статора:
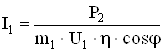 , (2.100)
, (2.100)
где Р2 – мощность на валу двигателя, Вт;
η – коэффициент полезного действия, о.е;
cosφ – коэффициент мощности;
U1 – фазное напряжение, В.
2.4.2 Потери в обмотке ротора
Потери в коротозамкнутой обмотке ротора определяются по формуле [13]:
![]() , (2.101)
, (2.101)
где r2 – активное сопротивление фазы обмотки ротора, Ом;
I2 – ток ротора, А.
Активное сопротивление фазы обмотки ротора:
![]() , (2.102)
, (2.102)
где rст – активное сопротивление стержня клетки, Ом;
rкл – активное сопротивление короткозамыкающего кольца, Ом;
Активное сопротивление стержня клетки:
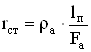 , (2.103)
, (2.103)
где ρа – удельное сопротивление алюминия обмотки ротора при ожидаемой температуре, Ом∙м.
Активное сопротивление короткозамыкающего кольца:
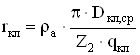 , (2.104)
, (2.104)
где Dкл,ср – средний диаметр короткозамыкающего кольца, м;
qкл – площадь поперечного сечения короткозамыкающего кольца, м2.
Коэффициент приведения тока кольца к току стержня:
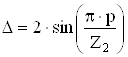 , (2.105)
, (2.105)
где p – количество пар полюсов.
Ток в обмотке ротора:
![]() , (2.106)
, (2.106)
где ki – коэффициент, учитывающий влияние тока намагничивания и сопротивления обмоток на отношение I1/I2;
νi – коэффициент приведения токов.
Коэффициент, учитывающий влияние тока намагничивания и сопротивления обмоток на отношение I1/I2:
![]() . (2.107)
. (2.107)
Коэффициент приведения токов:
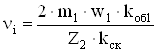 , (2.108)
, (2.108)
где kоб1 – обмоточный коэффициент обмотки статора;
kск – коэффициент скоса пазов ротора.
2.4.3 Потери в стали пакета статора
При расчете электрических машин потери в стали, определяют через массу стали и удельные потери, которые в свою очередь определяются значением магнитной индукции в стали и частотой питающего напряжения [13,14,15]. Такой способ определения потерь неудобен из-за того, что необходимо знать значение магнитной индукции в сердечнике статора.
![]() , (2.109)
, (2.109)
где РΣ – суммарная мощность потерь в двигателе, Вт;
Рмех – мощность механических потерь, Вт;
Рдоб – мощность добавочных потерь, Вт.
Суммарная мощность потерь в двигателе:
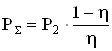 . (2.110)
. (2.110)
Мощность механических потерь [13]:
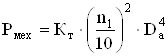 , (2.111)
, (2.111)
где Кт – коэффициент механических потерь.
Коэффициент механических потерь для двигателей с 2 р=2
![]() , (2.112)
, (2.112)
при 2 р≥4 Кт=1.
Мощность добавочных потерь:
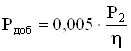 . (2.113)
. (2.113)
3. Реализация тепловой модели асинхронного двигателя в программном пакете Matlab
3.1 Переход к операторной форме
Для решения системы дифференциальных уравнений (1.20) на ЭВМ при помощи приложения Simulink, входящего в состав пакета MatLab, представим ее в операторной форме. Следует заметить, что недостатком приложения Simulink является отсутствие задания начальных условий в блоке передаточных функций. Поэтому при преобразовании (1.20) необходимо учесть начальные условия, то есть начальные температуры меди и стали.
В системе (1.20) присутствуют превышения температур меди и стали, которые равны:
![]() , (3.1)
, (3.1)
![]() . (3.2)
. (3.2)
Подставив (3.1) и (3.2) в (1.20) и раскрыв скобки получим:
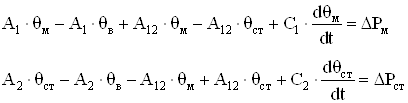 (3.3)
(3.3)
Представим систему (7.3) в операторной форме, по правилам преобразования Лапласа:
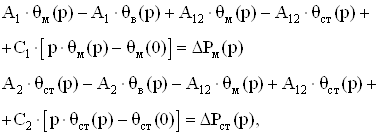 (3.4)
(3.4)
где θм(0) – начальная температура меди, 0С;
θст(0) – начальная температура стали, 0С;
Сгруппируем неизвестные θм(р) и θст(р) в левых частях уравнений (3.4), а остальные члены в правых частях:
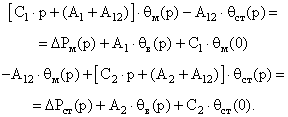 (3.5)
(3.5)
Представим систему (3.5) в матричной форме:
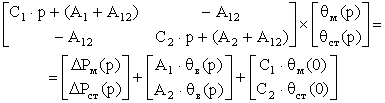 (3.6)
(3.6)
Решим систему (3.6) методом наложения относительно неизвестных θм(р) и θст(р). Решение имеет вид:
![]() , (3.7)
, (3.7)
![]() , (3.8)
, (3.8)
где
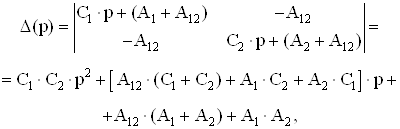
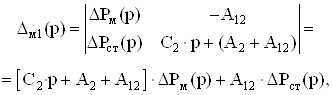
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |