Дипломная работа: Моделирование нагрева асинхронного двигателя

Дипломная работа: Моделирование нагрева асинхронного двигателя

Введение

Нестационарные тепловые процессы в электрических машинах имеют место при их эксплуатации. Ими сопровождаются режимы пуска, отключения, торможения, изменения нагрузки и частоты вращения машин. Большое значение процессы нестационарного нагрева имеют при перегрузках по току и напряжению, при частых и затяжных пусках двигателей, а так же при работе их в заторможенном состоянии.

Особенностью нестационарных тепловых режимов, или тепловых переходных процессов, в электрических машинах является их инерционность, проявляющаяся в значительном отставании изменений температуры от электромеханических переходных процессов. Благодаря этому машины могут выдерживать в течение некоторого времени воздействие перегрузок, токов короткого замыкания и других ненормальных условий. Учет тепловой инерционности в расчетах нестационарного нагрева является обязательным условием достоверности результатов.

Повышенная температура электрических машин влияет на долговечность изоляции обмоток, на работу подшипников и др. Повышенная температура обмоток вызывает тепловое старение изоляции, приводящее к необратимому снижению электрической и механической прочности. Правило Монтзингера гласит, что повышение температуры на 8–100 С сокращает срок службы изоляции в два раза.

Основной целью данной работы является создание тепловой модели для выбора асинхронного двигателя по нагреву. Данная модель является упрощенным представлением процессов нагрева и охлаждения двигателя. Суть модели заключается в том, что, задавая характер изменения нагрузки во времени на входе, на выходе имеем кривую изменения температуры меди обмоток или стали статора.

1. Обзор литературы

1.1 Фундаментальные законы теплопередачи

В основе математической модели нагрева двигателя лежит основной закон теплопроводности [1,2,3,4,5], сформулированный Фурье в итоге анализа экспериментальных данных. Данный закон устанавливает количественную связь между тепловым потоком и разностью температур в двух точках тела: количество переданной теплоты пропорционально градиенту температуры, времени и площади сечения F, перпендикулярного к направлению распространения теплоты.

Если количество переданной теплоты отнести к единице времени, то сформулированная зависимость выразится следующим образом:

, (1.1)

где р – количество переданной теплоты, отнесенное к единице времени, то есть мощность;

λ – коэффициент теплопроводности;

F – площадь сечения, перпендикулярного к направлению распространения теплоты;

θ – температура точек тела.

Знак «минус» в (1.1) означает, что передача теплоты происходит в сторону, противоположную направлению градиента, то есть в сторону понижения температуры.

Коэффициент теплопроводности λ в уравнении (1.1) является физическим параметром и характеризует способность вещества проводить теплоту.

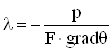, (1.2)

.

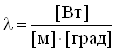Аналитическое решение, полученное путем непосредственного интегрирования уравнения (1.1), дает возможность вычислить температуру в любой точке системы. Однако решение уравнения в частных производных является довольно громоздким и слишком усложняет задачу. Поэтому на практике, для упрощения решения широко используется метод конечных разностей [3]. Сущность метода заключается в том, что в дифференциальном уравнении производные искомой функции заменяются приближенным соотношением между конечными разностями в отдельных узловых точках температурного поля. В результате такой замены получаем уравнение в конечных разностях, решение которого сводится к выполнению простых алгебраических операций:

, (1.3)

где δ – расстояние между исследуемыми точками;

Δθ – падение температуры на длине δ.

Для решения задач по определению температурного поля используют дифференциальное уравнение теплопроводности [1,2,3,4], которое выводится на основе закона сохранения энергии и закона Фурье. При выводе уравнения рассматривается нестационарное трехмерное температурное поле в однородном твердом теле, с распределенными по объему источниками теплоты. В пределах рассматриваемого тела берется элементарный объем dV=dx∙dy∙dz (рисунок 1.1), достаточно малый для того, чтобы считать физические параметры в нем постоянными, а потери – равномерно распределенными и пренебречь производными выше второго порядка от температуры θ по координатам.

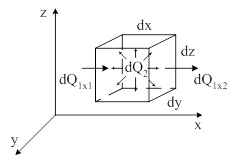
Рисунок 1.1 – Элементарный объем dV

Для элементарного объема dV составляется тепловой баланс за элементарный промежуток времени dt. Тепловой баланс является следствием закона сохранения энергии при допущении, что в энергетическом процессе не участвуют другие виды энергии, кроме тепловой:

, (1.4)

где dQ1 – тепловой поток, притекающий в объем dV за счет теплопроводности;

dQ2 – мощность источников теплоты, действующих внутри объема;

dQ – повышение внутренней энергии в объеме dV.

На рисунке 1.1 показаны только тепловые потоки, направленные вдоль оси x. Поток, притекающий слева, исходя из закона Фурье:

, (1.5)

тепловой поток, проходящий через противоположную грань (с учетом изменения производной ∂θ/∂x на интервале dx):

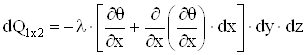. (1.6)

Результирующий приток теплоты за единицу времени вдоль оси x:

. (1.7)

Аналогично для других координатных осей:

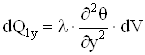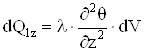; . (1.8)

Суммарный тепловой поток, притекающий в объем dV за счет теплопроводности:

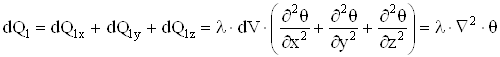. (1.9)

Мощность источников теплоты, действующих внутри объема:

, (1.10)

где р0 – мощность потерь в единице объема.

Изменение внутренней энергии в объеме dV:

, (1.11)

где с – удельная теплоемкость тела;

ρ – плотность материала тела.

Подставив (1.9), (1.10), (1.11) в (1.4) и проведя некоторые преобразования, получаем дифференциальное уравнение теплопроводности в частных производных:

. (1.12)

где  – слагаемое, описывающее изменение теплосодержания тела;

 – слагаемое, обуславливающее тепловой поток, притекающий в систему за счет теплопроводности;

 – слагаемое, обуславливающее внутреннее тепловыделение.

Рассмотрим процесс нагрева тела с собственным тепловыделением мощностью P, с поверхности S которого происходит теплоотдача конвекцией и излучением при коэффициенте теплоотдачи α [1,3,5]. Для упрощения математического описания процесса вводятся следующие допущения:

1.  Тело обладает неограниченной теплопроводностью, что приводит к отсутствию градиента температуры по любому направлению в его объеме.

2.  Температура окружающей среды θс неизменна, то есть окружающая среда обладает неограниченной теплоемкостью.

3.  Коэффициент теплоотдачи α между поверхностью машины и окружающей средой не зависит от места и длительности протекания процесса.

Уравнение теплового баланса составляется на том основании, что теплота, выделившаяся за элементарный промежуток времени dt, частично идет на изменение собственного теплосодержания тела и частично отводится в окружающую среду. В соответствии с этим уравнение теплового баланса имеет вид [1,3,5]:

, (1.13)

где ΔP – выделяемые в данном объеме потери мощности;

θ – температура тела;

θс – температура окружающей среды;

c – удельная теплоемкость;

G – масса исследуемого объема тела;

α – коэффициент теплоотдачи с единицы площади поверхности;

F – площадь поверхности охлаждения.

В правой части уравнения (1.13) первое слагаемое обуславливает повышение температуры тела, а второе – обмен теплотой с окружающей средой.

После преобразования уравнение теплового баланса (1.13) принимает вид:

, (1.14)

где C=с∙G – теплоемкость тела;

А=α∙F – коэффициент теплоотдачи тела.

1.2 Обзор методов теплового расчета и существующих моделей

В соответствии с разнообразием условий теплоотвода для теплового расчета электрических двигателей используются различные методы [4]:

1.  Метод точного или приближенного аналитического решения уравнений для трех- или двухмерных температурных полей обычно применяется при значительной неравномерности поля. При этом зачастую требуются определенные упрощения геометрической формы и граничных условий в математической модели.

2.  Численный метод сеток применяется в подобных случаях, но не требует значительных упрощений формы рассчитываемых областей пространства.

3.  Метод одномерного температурного поля применяется для расчета распределения температуры по длине обмоток и других частей электрических машин. Основан на приведении трех- и двухмерных полей к одномерному путем упрощенного представления теплопередачи вдоль всех осей координат, кроме одной, с помощью дискретных параметров (тепловых сопротивлений).

4.  Метод эквивалентных тепловых схем (ЭТС) получил наибольшее распространение ввиду простоты и достаточной точности расчета. Недостаток метода заключается в том, что он дает не полную картину температурного поля, а только некоторые средние значения температуры для отдельных элементов машины.

Данный метод основан на использовании тепловых сопротивлений [1], которые соединяются в тепловую сеть, имитирующую реальные пути передачи тепловых потоков в машине, и предполагает аналогию теплового потока с электрическим током, основанную на одинаковой форме основного закона теплопроводности (закон Фурье) [6]

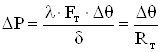 (1.15)

и электрического тока (закон Ома)

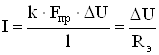, (1.16)

где Fт – площадь сечения, перпендикулярного распространению теплоты;

λ – коэффициент теплопроводности;

Δθ – падение температуры на длине δ;

Rт – тепловое сопротивление данного участка на пути теплового потока;

k – удельная электрическая проводимость;

ΔU – разность потенциалов на длине проводника l с сечением Fпр;

Rэ – электрическое сопротивление.

Узлы тепловой схемы имитируют отдельные части двигателя. Если в какой-либо части двигателя присутствуют распределенные по объему источники теплоты, то при составлении эквивалентной тепловой схемы они заменяются сосредоточенным источником (источником теплового потока), помещенным в узел, имитирующий эту часть. Узлы с внутренним тепловыделением на схеме обозначаются кружками, узлы без тепловыделения – точками.

Для детального расчета значений температур используют подробные эквивалентные тепловые схемы. Так, например в [2] приводится тепловая схема закрытого обдуваемого двигателя (рисунок 1.2). Система уравнений для данной схемы в установившемся режиме:

 (1.17)

где m – количество узлов эквивалентной тепловой схемы;

θв – температура воздуха снаружи машины;

Λki=1/Rki – тепловая проводимость соответствующего участка схемы;

Рi – потери в i-ом узле.

Отметим, что коэффициент теплоотдачи тела А в (1.14) и тепловые проводимости Λ в (1.17) имеют одинаковый физический смысл и размерность. Для расчета нестационарного режима используется та же тепловая схема, но каждый узел соединяется через емкость с внешним воздухом [4]. В этом случае электрическая емкость эквивалентна теплоемкости тела. Система уравнений для нестационарного режима:

 (1.18)

где Сi – теплоемкость соответствующего узла схемы.

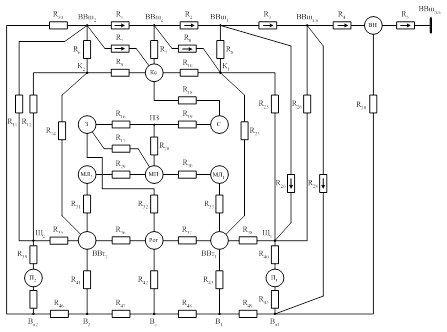
Рисунок 1.2 – ЭТС закрытого обдуваемого двигателя, учитывающая неоднородность температуры корпуса

Однако авторы [4] замечают, что пользоваться подробными схемами с большим количеством узлов целесообразно лишь в редких случаях (например, при проектировании системы охлаждения машины). В практических расчетах конкретных машин удобнее использовать упрощенные эквивалентные тепловые схемы. Упрощения состоят в том, что симметричные узлы подробной схемы, находящиеся в приблизительно одинаковых условиях, объединяются (лобовые части обмотки, воздух внутри машины, подшипниковые щиты) и эквивалентными преобразованиями тепловая схема преобразовывается в схему с меньшим количеством узлов – источников тепловыделения. Объединение узлов, по сути, является заменой нескольких источников тепловыделения, сгруппированных по определенным признакам, в один. Так, в [4,9] предлагается приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя (рисунок 1.3).

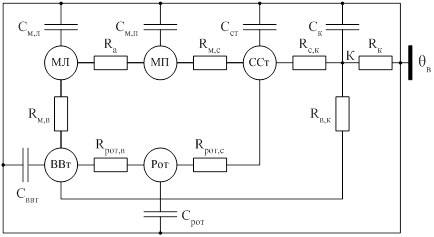
Рисунок 1.3 – Приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя

Данная схема имеет шесть узлов: МЛ – лобовая часть обмотки, МП – пазовая часть обмотки, ВВт – воздух внутри машины, Рот – ротор, ССт – сталь сердечника статора, К – корпус двигателя (станина и подшипниковые щиты). Система уравнений нестационарного режима для схемы (см. рисунок 1.3) имеет вид [4,9]:

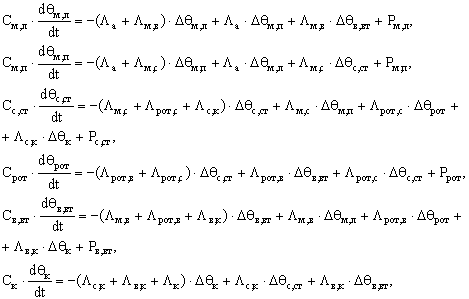
где Δθм,л – превышение температуры лобовых частей обмотки;

Δθм,п – превышение температуры пазовой части обмотки;

Δθс,ст – превышение температуры стали пакета статора;

Δθрот – превышение температуры ротора;

Δθв,вт – превышение температуры воздуха внутри машины;

Δθк – превышение температуры корпуса;

См,л – теплоемкость лобовых частей обмотки;

См,п – теплоемкость пазовой части обмотки;

Сс,ст – теплоемкость стали пакета статора;

Срот – теплоемкость ротора;

Св,вт – теплоемкость воздуха внутри машины;

Ск – теплоемкость корпуса;

Рм,л – мощность электрических потерь в лобовых частях обмотки;

Рм,п – мощность электрических потерь в пазовой части обмотки;

Рс,ст – мощность потерь в стали статора на вихревые токи и гистерезис;

Ррот – мощность электрических потерь в роторе;

Рв,вт – мощность механических и добавочных потерь;

Λа – тепловая проводимость между лобовой и пазовой частями обмотки;

Λм,с – тепловая проводимость между пазовой частью обмотки и сердечником статора;

Λм,в-тепловая проводимость между лобовыми частями обмотки и воздухом внутри машины;

Λрот,в-тепловая проводимость между ротором и внутренним воздухом; Λрот,с – тепловая проводимость между ротором и сердечником статора; Λв,к – тепловая проводимость между воздухом внутри машины и корпусом;

Λс,к – тепловая проводимость между сердечником статора и корпусом;

Λк – тепловая проводимость между корпусом и внешним воздухом.

Системы дифференциальных уравнений (1.18) и (1.19), описывающие процессы нагрева двигателя, по сути, являются тепловыми моделями асинхронного двигателя. Основные факторы, определяющие точность расчета по уравнениям (1.18) и (1.19) следующие:

– точность задания источников теплоты, то есть потерь;

– точность определения тепловых проводимостей Λ, которые в свою очередь зависят:

а) от коэффициентов теплопроводности λ, которые подвержены значительному разбросу по технологическим причинам, под влиянием появления воздушных промежутков и т.п.;

б) от коэффициентов теплоотдачи α, поскольку имеющиеся для их определения эмпирические формулы и графики не могут учесть всех влияющих факторов и условий.

В связи с этим, а так же для сокращения объема вычислений, рядом авторов [7,8,9,10,11,12] предложены упрощенные математические модели нагрева асинхронного двигателя.

Так в [7,8] предложена тепловая модель двигателя, состоящая из двух цилиндров (рисунок 1.4).

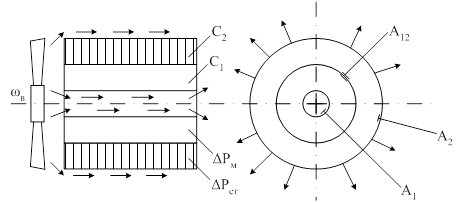
Рисунок 1.4 – Упрощенная модель двигателя как тела нагрева

Внешний цилиндр с теплоемкостью С2 моделирует массу железа машины, внутренний с теплоемкостью С1 – обмотки статора. Мощность теплового потока от стали к окружающей среде пропорциональна коэффициенту А2. Во внутреннем цилиндре предусмотрен канал, моделирующий отвод теплоты потоками воздуха от внутренних частей машины. Мощность теплового потока от меди статора к окружающей среде пропорциональна коэффициенту А1. Теплопередача между медью и сталью определяется коэффициентом А12, моделирующим термическое сопротивление изоляции.

Данной модели соответствует система уравнений [7,8]:

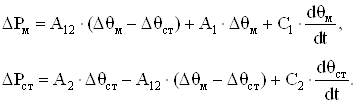 (1.20)

где Δθм и Δθст – превышения температуры меди и стали соответственно над температурой окружающего воздуха.

В [9] авторы получают уравнения, описывающие поведение температуры обмотки двигателя, путем аналитического решения системы (1.19)

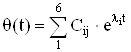, (1.21)

и замены решения (1.21), состоящего из шести экспонент, приближенным решением, состоящим из двух экспонент:

, (1.22)

где θ(t) – текущее превышение температуры обмотки;

θуст – превышение температуры в установившемся режиме;

Ii – текущее значение тока статора;

Iн – номинальный значение тока статора;

Tmax – максимальная постоянная нагрева (постоянная нагрева стали магнитопровода);

Tmin – минимальная постоянная нагрева (постоянная нагрева обмотки);

Kн – коэффициент нагрева, учитывающий составляющую превышения температуры стали в превышении температуры обмотки.

По такому же принципу в [9] рассчитывается охлаждение двигателя после отключения его от сети. Зависимость температуры от времени при охлаждении двигателя описывается следующим выражением:

, (1.23)

где To max – максимальная постоянная охлаждения;

To min – минимальная постоянная охлаждения;

Kо – коэффициент охлаждения.

Значение θуст определяется решением (1.19) для установившегося режима, то есть при dθ/dt=0.

По сути дела, в модели [9] двигатель так же представлен двумя телами нагрева: обмоткой статора с минимальной постоянной нагрева Tmin и сталью машины с максимальной постоянной нагрева Tmax. Недостатком данной модели является отсутствие задания начальных условий.

Самой простой тепловой моделью электродвигателя является представление его одним телом нагрева [7,8,10,11]. При этом вводятся следующие допущения:

1.  Электродвигатель имеет бесконечно большую теплопроводность и, как следствие, одинаковую температуру по всему объему;

2.  Количество теплоты, которым электродвигатель обменивается с окружающей средой, пропорционально разности температур двигателя и окружающей среды;

3.  Тепловые параметры электродвигателя и окружающей среды постоянны и не связаны с температурой двигателя (это обстоятельство обеспечивает линейность тепловой модели).

В этом случае уравнение, описывающее нагрев двигателя:

. (1.24)

Решение этого уравнения при постоянстве потерь двигателя ΔP=const и, следовательно, постоянном установившемся превышении температуры:

, (1.25)

где Δθ(t) – текущее превышение температуры двигателя над температурой окружающей среды;

Δθуст – установившееся превышение температуры двигателя;

Δθ0 – начальное превышение температуры двигателя;

Тθ=С/А – постоянная времени нагрева.

В силу того, что асинхронный двигатель представляет собой сложную термодинамическую систему, неоднородную по своим тепловым параметрам, последняя модель является довольно грубым приближением.

Страницы: 1, 2, 3, 4, 5