Дипломная работа: Разработка оборудования для уплотнения балластной призмы

где BМ – максимально допустимый вылет исполнительных органов в сторону междупутья, м (BМ=2,050 м); Lшп – длина шпалы, м (Lшп=2,75); вК – вылет клина относительно корпуса плиты, м (вk = - 0,085 м); δ – заход клина под торцы шпал, м (δ= - 0,17 м).

.

Конструктивно принято Bк = 0,35 м.

В процессе разработки возбудителя колебаний размеры корректируются.

При транспортировке машины плита не должна выходить за приделы габаритов подвижного состава.

Эскизная компоновка корпуса виброплиты показана на рисунке 2.3.

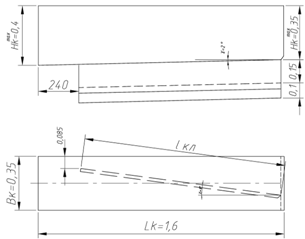
Рисунок 2.3 - Эскизная компоновка корпуса виброплиты

2.1.3 Разработка возбудителя колебаний

Для дебалансного возбудителя рассчитывается требуемая вынуждающая сила FВ и, соответственно, конструкция дебалансов, обеспечивающих колебания виброплиты, с заданной амплитудой.

При вращении дебалансов с угловой частотой ω и амплитудой Sa суммарная вынуждающая сила составит:

, (2.10)

где mn – приведенная масса колеблющихся элементов, кг; ωo – частота свободных колебаний плиты с учётом жёсткости балласта, с-1; h – коэффициент демпфирования, с-1.

Находим mn:

mn = an ·m, (2.11)

где m –масса корпуса плиты с вибровозбудтелем, кг (m = 400 кг); aп – коэффициент приведения (aп=1,15 [1]).

mn = 1,15·400=460 кг.

Находим ωo:

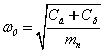 ,(2.12)

где Cр – приведенный коэффициент жёсткости рессорной подвески (принят Cр = 1·106 Н/м); Cб – приведенный коэффициент жёсткости балласта, Н/м.

Cб = Cуд ·Z ·a · l , (2.13)

где Z – заглубление под шпалу, м (Z=0,1 м); a – толщина клина, м (a=0,1 м); l – длина клина, м (l=1,35 м); Cуд – удельный коэффициент жёсткости балласта, Н/м4 , принимается по графику, при:

 (Cуд= 3·107 Н/м4 [1]).

Cб = 3·107 ·0,1·0,1·1,35 = 40,5 ·104 Н/м .

Тогда:

 .

Далее находится h:

, (2.14)

где bб , bр – соответственно коэффициент сопротивлений балласта и рессор, Н·с/м (принят bр = 5·103 Н·с/м [1]).

bб = bуд·Z ·a · l, (2.15)

где bуд – удельный коэффициент вязкостных сопротивлений, Н·с/м4, принимается по графику [1], при :

 bуд = 12 · 104 Н·с/м4.

bб = 12·104·0,1·0,1·1,35 = 1,62·103 Н·с/м .

Тогда:

.

В итоге по формуле (2.10) получили:

.

Принята FВ = 90 кН.

По найденной FВ и принятой компоновке вибровозбудителя найдём вынуждающую силу одного дебаланса FВ’:

FВ’ = FВ / n,(2.16)

где n – принятое число дебалансов (n=4).

FВ’ = 90 / 4 = 22,5 кН .

Предварительно назначается расчётная длина вала дебаланса (рисунок 2.4) равная lв = 0,22.

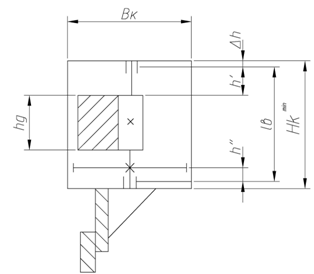
Рисунок 2.4 – Схема дебаланса

Для нахождения диаметра вала строится эпюра изгибающего момента. Для этого находятся реакции в точках опоры (рисунок 2.5)

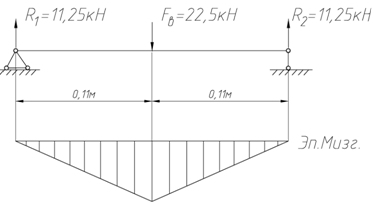
Рисунок 2.5 –Эпюра изгибающего момента

Максимальный изгибающий момент равен:

Mmax = R1 · 0,11 =11,25 · 0,11 =1,24 кН · м .

Прочность вала:

,(2.17)

где W – момент сопротивления при изгибе, м3 ; (для круглого сечения ); [σ] – допускаемое напряжение, МПа .

,(2.18)

где σFlim – предел длительной выносливости, МПа; SF – коэффициент безопасности (для Ст 45 - SF = 1,75 , [2] стр. 90).

Для стали 45 :

σFlim =1,8 НВ,(2.19)

где НВ – твёрдость стали (для стали 45 HB = 248,5 , источник [2] стр.426).

Допускаемое напряжение равно:

[σ] = (1,8·248,5)/1,75 =255,6 МПа.

Находится диаметр вала по формуле:

;(2.20)

.

Принят d = 40 мм ([2] стр. 296)

2.1.3.1 Компоновка дебалансов

Неуравновешенные части дебалансов в сечении имеют форму кругового сектора. Значение r0 (расстояние от оси вращения до центра тяжести дебаланса) зависит от угла сектора φ0 внешнего Rв и внутреннего rв радиусов дебаланса (рисунок 2.6).

Угол φ0 по рекомендациям [1] назначается 120˚. Радиус Rв предварительно определяется выражением:

Rв = 0,5· ВК – δД – bК, (2.21)

где δД – зазор между дебалансом и стенкой корпуса, м (δД = 0,045 м); bК – толщина корпуса виброплиты, м (bК = 0,01 м).

Rв = 0,5·0,35 – 0,02 – 0,01 = 0,12 м.

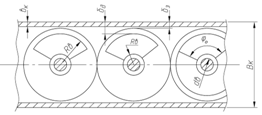
Рисунок 2.6 – Схема компоновки дебалансов

Расстояние от оси вращения до центра тяжести дебаланса:

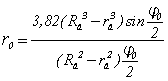.(2.22)

Внутренний радиус дебаланса:

,(2.23)

где δст – ширина ступицы, м (принимается конструктивно δст=0,02 м)

.

Тогда

.

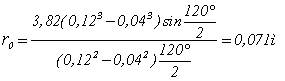При требуемых силе Fв’ , частоте ω и установленном r0 определяется масса неуравновешенной части дебаланса:

;(2.24)

.

Площадь дебаланса, м2 :

;(2.25)

.

Длина дебаланса, м:

 ,(2.26)

где ρ – плотность металла, кг/м3 (ρ =7800 кг/м3).

.

2.2 Мощность, необходимая при виброобжатии балласта

Затраты мощности при виброподбивке шпал представлены в виде:

Рв = Рб + Pвс, (2.27)

где Рб – средняя мощность, необходимая для преодоления сопротивлений колебаниям виброплиты от балласта и рессорной подвески, Вт; Pвс – мощность, необходимая для преодоления внутренних сопротивлений вибровозбудителя, Вт.

,(2.28)

где φ - фаза вынужденных колебаний по отношению к фазе возмущающей силы, град; Fв – максимальная вынуждающая сила, Н (Fв=90·103Н).

,(2.29)

где h – коэффициент демпфирования, с-1 (h = 7,2 с-1); ω0 – частота свободных колебаний плиты с учётом жёсткости балласта, с-1 (ω0=55,26 с-1).

По формуле (2.28) находится:

.

Мощность  находится по формуле:

,(2.30)

где P0 – мощность, необходимая для преодоления диссипативных сопротивлений вращению, Вт.

Р0 =0,5·Fв · dв·ω ·fn, (2.31)

где fn – приведённый коэффицент трения в подшипниках дебелансного вала, fn = 0,001 ( [3] стр.148).

P0 = 0,5·90 ·103·0,04 ·188,4·0,001 = 339,12 Вт

Находится PВМ :

PВМ = 0,02 · P0 , (2.32)

PВМ = 0,02 · 339,12 = 6,7 Вт

Находим Р33 по формуле:

,(2.33)

где ηз – КПД зубчатой передачи синхронизатора (ηз = 0,96 – [2] стр. 23); m – количество зубчатых зацеплений (m=4).

Pзз= (4246 +339,12) · (1 – 0,964) = 690,7 Вт.

Тогда:

Pвс’ = 339,12 + 6,7 + 690,7 = 1036,8 Вт.

В итоге суммарные затраты мощности равны:

Pв = 1036,6 + 4246 = 5282,3 Вт.

В некоторые моменты работы виброплиты могут возникнуть ситуации, такие как совпадение фазы вынужденных колебаний с фазой возмущающей силы.

Максимально возможные значения Рб возможно при sin2 φ0 =1:

.

Максимально возможные потери мощности в зубчатом зацеплении:

P33max = (25570+339,12)(1-0,964) = 3801,1 Вт.

Тогда мощность PВС’ max:

PВС’ max = 339,12 + 6,7 + 3801,1 = 4146,9 Вт.

В итоге максимально возможная мощность, затрачиваемая на виброподбивку шпал равна:

Pв max = 25570 + 4146,9 = 29716,9 Вт.

Для того чтобы учесть возрастание сопротивления на виброподбивку шпал, при попадании плиты в резонанс, при выборе двигателя возьмём среднее значение мощности Pв ср:

Pв ср = (5282,6 +29716,9)/2 =17499,7 Вт ≈17,5 кВт.

Потребная мощность двигателя вибровозбудителя подбивочной плиты, кВт:

Pв ср = Pв ср / ηn,(2.34)

где ηn – КПД передачи от двигателя до ведущего вала вибровозбудителя (ηn = 0,98).

Pдв = 17,5/0,98 =17,85 кВт.

Выбирается асинхронный двигатель с фазным ротором ([2] стр.27) таблица 2.1:

Таблица 2.1 – Характеристики асинхронного двигателя 4А160М2У3

Типоразмер	Мощность PH, кВт	Синхр. частота вращения, об/мин	Скольжение, %	nH, oб/мин	Тmax/ Тном
4А160М2У3	18,5	1500	2,2	1467	1,4

Находится крутящий момент на валу двигателя, H·м:

Тmax = 9550 · PH / nH ;(2.35)

Тmax = 9550 · 18,5/ 1467= 120,43 H·м.

Учитывая разность частоты вращения валов дебалансов и частоты вращения вала двигателя устанавливается дополнительный вал с зубчатым колесом повышающим частоту вращения вала дебаланса (рисунок 2.7).

Для передачи крутящего момента от вала двигателя к ведущему валу дебалансов устанавливается карданный вал от ГАЗ – 53 [8], который рассчитан на Pmax = 84,6 кВт ; Тmax = 284,4 H·м ; n = 2000 об/мин.

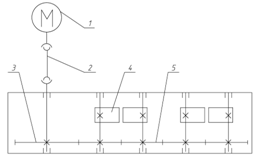
1 – двигатель; 2 – карданный вал; 3 – ускоряющее зубчатое колесо; 4 – дебаланс; 5 – синхронизирующие зубчатые шестерни.

Рисунок 2.7 – Привод виброплиты

2.3 Расчёт цилиндрической зубчатой передачи внешнего зацепления

Исходные данные:

Максимальный крутящий момент на тихоходном валу Тmax I = 120,43 H·м

Частота вращения ведущего (ведомого) вала nII = 1800 об/мин

Частота вращения ведомого (ведущего) вала nI = 1467 об/мин

Материал шестерни ст 40Х У

Материал колесаст 40Х ТВ4

Передаточное отношение:

u21 = nII / nI =1800/1467 =1,22.

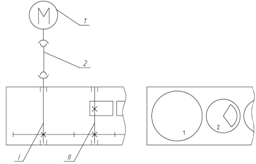
I – тихоходный вал; 1 – зубчатое колесо; II – быстроходный вал; 2 – шестерня.

Рисунок 2.8 – Зубчатая передача внешнего зацепления

Расчёт произведён на ЭВМ (программа ДМ – 1).

2.3.1 Алгоритм расчёта зубчатой передачи (силовой расчёт).

1) Определяется по контактным напряжениям межосевое расстояние aW в мм по формуле :

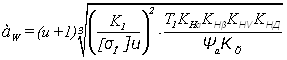, (2.35)

где u – передаточное число рассчитываемой передачи (u = 1,22); K1 – вспомогательный численный коэффициент (K1 = 315 [2]); [σH] – допускаемое контактное напряжение, МПа; Т1 – крутящий момент на валу колеса, H·мм; KНα – коэффициент распределения нагрузки (KНα = 1 [2]); KНβ – коэффициент концентрации нагрузки ( [2] ст 92) ;KНV – коэффициент динамичности [2]; KНД – коэффициент долговечности лимитирующего колеса [2]; Ψa – коэффициент ширины венца, принимается из единого ряда [2 стр. 52] (Ψa = 0,2 …0,4); KХ – коэффициент, учитывающий смещение.

2) Ширина колеса в мм:

b2 = Ψa· aW.(2.36)

3) Модуль зацепления m в мм из расчёта на изгиб ориентировочно определяется по формуле:

,(2.37)

где K2 – численный коэффициент (для прямозубых колёс K2 = 5); KFα , KFβ , KFv ,KFД – коэффициенты, аналогичные KНα , KНβ , KНV , KНД определяются по [2]; [σF] – допускаемое изгибное напряжение лимитирующего колеса, МПа ([2] стр. 91).

4) Расчёты по формулам (2.35)…(2.36) составляют программу ДМ – 1. Машина выдаёт на печать исходные данные и величины aW ,b2 и m в миллиметрах. Полученные данные подлежат обработке.

Значения aW и b2 выбираются из единого ряда ([2], ст 51). Допускается их округление по ГОСТ 6636 – 69 ([2] ст 296). Модуль округляется в большую сторону.

2.3.2 Алгоритм геометрического и проверочного расчёта зубчатой передачи

Определение чисел зубьев:

1) Суммарное число зубьев ZΣ:

ZΣ = 2·aW· cos β / m ,(2.38)

где β – угол наклона линии зуба.

Величина ZΣ округляется до ближайшего целого числа.

2) Число зубьев шестерни Z1 :

Z1 = ZΣ / (u + 1).(2.39)

3) Число зубьев колеса Z2:

Z2 = ZΣ – Z1.(2.40)

4) Окружная скорость колёс v, м/с:

 .(2.41)

5) Уточнённое передаточное число u 21:

u 21 = Z2 /Z1.(2.42)

6) Ширина шестерни b2, мм:

b2 = 1,1 b2.(2.43)

7) Межосевое расстояние, мм:

aW = 0,5·m(Z1 + Z2) + (Х1 + X2 – Δy)m ,(2.44)

где Х1 , X2 – коэффициенты смещения (Х1 = X2=0 [2]); Δy – коэффициент уравнительного смещения (Δy = 0 [2]).

8) Угол наклона линии зуба для прямозубых колёс β = 0.

9) Делительные диаметры d, мм:

d = m · z / cos β.(2.45)

10) Диаметр вершин d a, мм:

d a = d + (2 + 2x– 2Δy)m.(2.46)

11) Диаметр впадин d f , мм:

d f = d – (2,5 – 2x)m.(2.47)

12) Окружная толщина зубьев по делительной окружности St, мм:

St = (π/(2cos β) + 2x·tgα)m.(2.48)

13) Угол зацепления αW:

,(2.49)

где α – угол профиля (α = 20˚).

14) Торцевой коэффициент перекрытия εα:

 .(2.50)

15) Коэффициент суммарной длины контактных линий Zε:

.(2.51)

16) Угол наклона линии зуба по основной окружности βв:

.(2.52)

17) Коэффициенты формы сопряжённых поверхностей зубьев в полосе зацепления Zн:

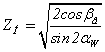.(2.53)

18) Рабочее контактное напряжение σн, мПа:

,(2.53)

где  - коэффициент, учитывающий механические свойства материалов сопрягаемых поверхностей (= 275) [14].

19) Отклонение рабочего контактного напряжения от допускаемого ∆σн, %:

.(2.54)

20) Окружное усилие Ft, H:

,(2.55)

где - начальный диаметр колеса, мм.

,(2.56)

где - начальный диаметр шестерни, мм.

.(2.57)

21) Радиальное усилие Fy, H:

. (2.58)

22) Осевое усилие Fa, H:

.(2.59)

23) Коэффициент перекрытия зубьев Yε :

Yε=1.

24) Коэффициент наклона зубьев Yβ :

Yβ=1.

25) Рабочее изгибное напряжение зубьев шестерни σF2, мПа:

.(2.60)

26) Рабочее изгибное напряжение колеса σF1, мПа:

.(2.61)

27) Максимальное контактное напряжение σн max, мПа:

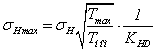.(2.62)

28) Максимальное изгибное напряжение σF max, мПа:

.(2.63)

Значения рассчитываемых величин представлены на распечатках результатов расчёта, сделанного на ЭBM (программа ДМ-1).

2.3.3 Результаты расчёта зубчатой передачи, выданные ЭВМ

2.3.4 Анализ результатов расчёта зубчатой передачи

Геометрические параметры округляем до сотых долей миллиметра.

По допускаемым и рабочим напряжениям делаем вывод, что прочность достаточна.

Усилие в зацеплении округляем с точностью до целых.

2.4 Уточнённый расчёт валов и выбор подшипников

Данный расчёт даёт более достоверные результаты, чем ориентировочный расчёт.

В этом разделе исходными данными являются: силы, действующие на колесо шестерни, расстояния между линиями действия всех сил, диаметры колёс.

Для наглядного представления изобразим аксонометрическую схему нагружения валов (рисунок 2.9).

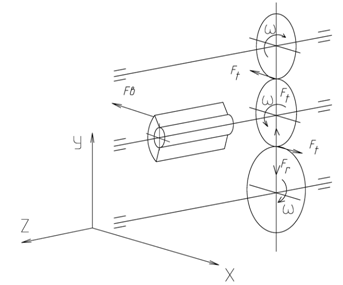
Рисунок 2.9 – Схема нагружения валов

2.4.1 Расчёт дебалансного вала

Для уточнённого расчёта выполним эскизную компоновку элементов вала (рисунок 2.10).

Предварительно назначаем подшипник по ГОСТ 5720 – 75: № 1608 с d=40 мм, D =90 мм, B =33 мм [2].

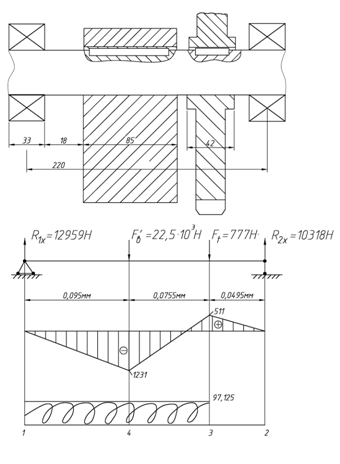
Рисунок 2.10 – Эскизная компановка элементов вала

На вал действуют две силы в направлении X (рисунок 2.10, б) F’в , Ft и крутящий момент T.

Составим уравнения суммы моментов относительно точек 1 и 2, найдём реакции в этих точках.

ΣM1=0;

.

ΣM2=0;

.

Находим изгибающий момент в т. 1, 2, 3 ,4 (Рисунок 2.10, в):

;

;

Страницы: 1, 2, 3, 4, 5, 6, 7, 8