Курсовая работа: Проектирование привода электролебёдки (редуктор)

YF2=3,62

zv1=39/cos311,48°= 41,44

YF1=3,69

Yb=1-β0/140                                                                                      (33)

Yb=1-11,48°/140=0,918

sF2=2×174950×3,62×1×0,918×1,11/(240,3×30×1,5) = 119,4 МПа

sF2= 119,4£200,85 Н/мм2

sF1=119,4(3,69/3,62) = 121,7 £[sF]2

sF1= 121,7 £ 213,21Н/мм2

Колесо и шестерня проходят проверку на изгиб.

Таблица 3.

Параметры первой ступени косозубой передачи

	Шестерня	Колесо
Материал	Сталь 45	Сталь 45
Твердость НВ	207	195
Допускаемое контактное напряжение [σн], Н/мм2	439,6	418
Допускаемое напряжение на изгиб [σF], Н/мм2	213,21	200,85
Ширина венца b, мм	34	30
Делительный диаметр d, мм	59,7	240,3
Диаметр впадин df, мм	55,95	236,55
Диаметр вершин dа, мм	62,7	243,3
Число зубьев z	39	157
Контактное напряжение σн, Н/мм2		412,7
Напряжение на изгиб σF, Н/мм2	121,7	119,4
Межосевое расстояние аw, мм	150
Угол наклона зубьев b, °	11,48
Фактическое передаточное число редуктора uф	4,03
Модуль передачи m	1,5

3.2.  Расчет второй ступени цилиндрического редуктора

3.2.1. Выбор материала и определение допускаемых напряжений

По таблице 3.2 [4,с.50] выбираем марку стали: 45 термообработка –нормализация.  Принимаем твёрдость шестерни НВ1=207, твёрдость колеса НВ2=195.

Допускаемое контактное напряжение:

 [σн.]1=1,8· 207+67= 439,6 Н/мм2

[σн.]2=1,8· 195+67= 418 Н/мм2

За расчётное допускаемое напряжение принимаем меньшее из двух допускаемых контактных напряжений [σн]=418 Н/мм2.

Допускаемое напряжение изгиба определяется:

 [σ F]1=1,03·207 = 213,21 Н/мм2

[σ F]2=1,03·195 = 200,85 Н/мм2

3.2.2. Определение значения межосевого расстояния

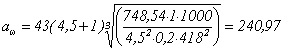мм

Полученное значение межосевого расстояния округляем до ближайшего по ГОСТ 6636-69  aω=240 мм.

3.2.3. Определение рабочей ширины венца колеса и шестерни

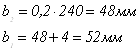
3.2.4. Определение модуля передачи

 мм

Полученное значение модуля округляет до ближайшего значения из стандартного ряда по ГОСТ 9563-60 m = 2,5 мм.

3.2.5. Определение суммарного числа зубьев и угла  наклона зуба

3.2.6. Определение числа зубьев шестерни и колеса

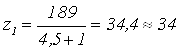
z2=189 – 34= 155

3.2.7. Определение фактического значения передаточного числа. Проверка передачи по передаточному числу

Du=(|4,56-4,5|)/4,5·100%=1,33% <4%

3.2.8. Определение фактического межосевого расстояния.

мм

3.2.9. Определение геометрических параметров колеса и шестерни

Делительные диаметры

d1=2,5×34/cos10,14°=86,4 мм

d2=2,5×155/cos10,14°=393,6 мм.

Диаметры вершин зубьев

da1=86,4+2×2,5= 91,4 мм

da2=393,6+2×2,5= 398,6 мм

Диаметры впадин зубьев

df1=86,4 – 2,5×2,5= 80,15мм

df2=393,6 – 2,5×2,5= 387,35 мм

3.2.10. Проверка зубьев шестерни и колеса на контактную выносливость

Кнα – коэффициент учитывающий распределение нагрузки между зубьями, по графику [4,с.63] находим Кнα = 1,11;

Kнυ – коэффициент, учитывающий динамическую нагрузку, определим по таблице 4.3. [4,с.62] Kнυ = 1,01;

Колесо и шестерня проходят проверку на контактную выносливость.

3.2.11. Проверка зубьев шестерни и колеса на выносливость при изгибе.

KFn - коэффициент, учитывающий динамическую нагрузку, KFn=1,04.

Значение YF1,2 определяем по таблице 4.4 [4,с.64] в зависимости от эквивалентного числа зубьев, zv1,2= z1,2/cos3β.

zv2=155/cos310,14°= 162,5

YF2=3,62

zv1=34/cos310,14°= 35,6

YF1=3,75

Yb=1-10,14°/140=0,928

sF2=2×748540×3,62×1×0,928×1,04/(393,6×48×2,5) = 110,7 МПа

sF2= 110,7£200,85 Н/мм2

sF1=110,7(3,75/3,62) = 114,7 £[sF]2

sF1= 114,7 £ 213,21Н/мм2

Колесо и шестерня проходят проверку на изгиб.

Таблица 4.

Параметры первой ступени косозубой передачи

	Шестерня	Колесо
Материал	Сталь 45	Сталь 45
Твердость НВ	207	195
Допускаемое контактное напряжение [σн], Н/мм2	439,6	418
Допускаемое напряжение на изгиб [σF], Н/мм2	213,21	200,85
Ширина венца b, мм	52	48
Делительный диаметр d, мм	86,4	393,6
Диаметр впадин df, мм	80,15	387,35
Диаметр вершин dа, мм	91,4	398,6
Число зубьев z	34	155
Контактное напряжение σн, Н/мм2		405,6
Напряжение на изгиб σF, Н/мм2	114,7	110,7
Межосевое расстояние аw, мм	240
Угол наклона зубьев b, °	10,14
Фактическое передаточное число редуктора uф	4,56
Модуль передачи m	2,5

Страницы: 1, 2, 3, 4