Курсовая работа: Проектирование привода электролебёдки (редуктор)

Курсовая работа: Проектирование привода электролебёдки (редуктор)

СОДЕРЖАНИЕ

1.  Техническое задание 2.  Энерго-кинематический расчет привода 3.  Расчет редуктора 4.  Подбор и проверочный расчет подшипников 5.  Смазывание редуктора 6.  Конструирование корпуса и деталей редуктора 7.  Подбор и проверочный расчет муфт 8.  Расчет шпоночных соединений 9.  Технический уровень редуктора Вывод Литература

1.  ТЕХНИЧЕСКОЕ ЗАДАНИЕ

Спроектировать привод электролебедки по схеме, представленной на рисунке 1.

Исходные данные для варианта 2:

w  Тяговое усилие каната F = 10 кН;

w  Скорость каната u = 0,42 м/с;

w  Диаметр барабана D = 150 мм;

w  Срок службы редуктора L = 5 лет.

2.  ЭНЕРГО-КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДА. ПОДБОР ЭЛЕКТРОДВИГАТЕЛЯ                        

2.1.  Выбор электродвигателя

,                                                                               (1)

где h - кпд привода;

 hм - кпд муфты, hм.=0,98;

 hп.к..- кпд подшипников качения, hп.к.= (0,99  ¸  0,995);  

 hз.п.- кпд закрытой передачи, hз.п.= (0,96  ¸  0,98).

h = 0,992·0,982·0,982=0,904

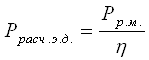,                                                                           (2)

где Р - расчётная мощность электродвигателя, кВт;

Рр.м. - мощность рабочей машины, кВт.

,                                                                                  (3)

где F - тяговое усилие каната, кН;

u - скорость каната, м/с.

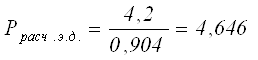кВт

кВт

По таблице [4, с.384] выбираем подходящий электродвигатель.

Таблица 1.

Типы двигателей

Мощность, кВт	Тип двигателя	Номинальная частота, об/мин
5,5	4А100L2У3	2880
	4А112М4У3	1445
	4А132S6У3	965
	4А132М8У3	720

2.2.  Определение общего передаточного числа привода и его разбивка по ступеням

u=u1·u2 ,                                                                                             (4)

где u – общее передаточное число привода;

u1 – передаточное число первой ступени;

u2 – передаточное число второй ступени.

Определим передаточное число привода для всех приемлемых вариантов типа двигателя.

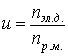                                                                        (5)

где nэ.д. – частота вращения вала электродвигателя, об/мин;

nр.м – частота вращения рабочей машины, об/мин.

                                                                    (6)

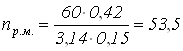об/мин

          

    

Из стандартного ряда передаточных чисел первой ступени u1 = 4.

          

           

Из стандартного ряда передаточных чисел второй ступени u2 = 4,5.

2.3.  Определение частоты вращения и моментов на валах

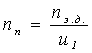                                                                                       (7)

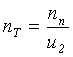                                                                                            (8)

где nт – частота вращения тихоходного вала редуктора, об/мин;

nб – частота вращения промежуточного вала редуктора, об/мин;

об/мин

об/мин

Проверка отклонения частоты вращения рабочей машины от расчетной.

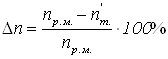< 5%                                                                (9)

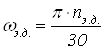                                                                        (10)

 где ωэ.д. – угловая скорость вала электродвигателя, с-1.

 с-1

 с-1

 с-1

P = T·ω,                                                                                            (11)

где Pэл – мощность электродвигателя, Вт;

       Tэд – крутящийся момент на валу электродвигателя, Н·м.

Н·м

Т1=Тэд·u1 ∙    ,                                                                  (12)

Т2=Т1·u2      ,                                                                  (13)

где Т1 – крутящийся момент промежуточного вала редуктора, Н·м;

Т2 – крутящийся момент тихоходного вала редуктора, Н·м.

Тп=46·4∙0,99∙0,98∙0,98=174,95 Н·м

Тт=174,95·4,5∙0,99∙0,98∙0,98=748,54 Н·м

Таблица 2.

Параметры привода

	Крутящий момент Т, Н×м	Частота n, об/мин	Угловая скорость w, с-1	Передаточное число u
Двигатель 4А250М6У3	46	965	101
Редуктор, промежуточной вал	174,95	241,25	25,25	4
Рабочий тихоходный вал	748,54	53,61	5,61	4,5

Вывод: в данном пункте был произведен энерго-кинематический расчет привода. Выбран асинхронный двигатель. Рассчитаны передаточные числа каждой ступени. Определены крутящие моменты, угловые скорости и частоты вращения на валах ступеней.

3.  РАСЧЁТ РЕДУКТОРА

3.1.  Расчет первой ступени цилиндрического редуктора

3.1.1. Выбор материала и определение допускаемых напряжений

По таблице 3.2 [4,с.50] выбираем марку стали: 45 термообработка –нормализация.  Принимаем твёрдость шестерни НВ1=207, твёрдость колеса НВ2=195.

Допускаемое контактное напряжение:

[σн]= (1,8· НВср+67)×КHL ,                                                                (14)

где [σн]- допускаемое контактное напряжение, Н/мм2;

КHL – коэффициент долговечности, КHL =1;

НВср – твердость детали.

[σн.]1=1,8· 207+67= 439,6 Н/мм2

[σн.]2=1,8· 195+67= 418 Н/мм2

За расчётное допускаемое напряжение принимаем меньшее из двух допускаемых контактных напряжений [σн]=418 Н/мм2.

Допускаемое напряжение изгиба определяется:

[σF]= 1,03· НВ×КFL         ,                                                                            (15)

где [σF] - допускаемое напряжение изгиба, Н/мм2;

KFL – коэффициент долговечности,  KFL=1;

[σ F]1=1,03·207 = 213,21 Н/мм2

[σ F]2=1,03·195 = 200,85 Н/мм2

3.1.2. Определение значения межосевого расстояния

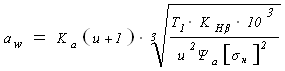,                                                (16)

где Kнβ – коэффициент неравномерности нагрузки по длине зуба, Kнβ = 1;

Ka – вспомогательный коэффициент: для косозубых передач    Ka=43;

ψa – коэффициент ширины венца колеса, для несимметричных редукторов, ψa=0,2….0,25, принимаем ψa= 0,2;

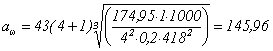мм

Полученное значение межосевого расстояния округляем до ближайшего по ГОСТ 6636-69  aω=150 мм.

3.1.3. Определение рабочей ширины венца колеса и шестерни

                                                                                     (17)

                                                                          (18)

где  - рабочая ширина венца шестерни, мм;

        - рабочая ширина венца колеса, мм.

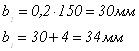
3.1.4. Определение модуля передачи

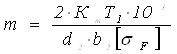   ,                                                                   (19)

где m – модуль передачи, мм;

Кm – вспомогательный коэффициент, для косозубой передачи Кm = 5,8;

d2 – делительный диаметр колеса, мм.

                                                                                          (20)

 мм

Полученное значение модуля округляет до ближайшего значения из стандартного ряда по ГОСТ 9563-60 m = 1,5 мм.

3.1.5. Определение суммарного числа зубьев и угла  наклона зуба

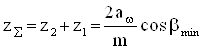,                                                               (21)

Принимаем минимальный угол наклона зуба βmin равным 10°.

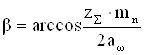                                                                             (22)

где zΣ – суммарное число зубьев;

z1,z2 – числа зубьев шестерни и колеса;

β – действительное значение угла наклона зуба.

3.1.6. Определение числа зубьев шестерни и колеса

                                                                                      (23)

z2=196 – 39= 157

3.1.7. Определение фактического значения передаточного числа.

Проверка передачи по передаточному числу

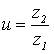                                                                                                   (24)

Δu=(|uт-u|/uт)·100%  <4% ,                                                                       (25)

где u – фактическое значение передаточного числа редуктора;

uт – теоретическое значение передаточного числа взятого из стандартного ряда редукторов, uт=4;

Du – отклонение фактического значения передаточного числа редуктора от заданного, %.

Du=(|4,03-4|)/4·100%=0,75% <4%

3.1.8. Определение фактического межосевого расстояния.

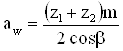                                                                                 (26)

мм

3.1.9. Определение геометрических параметров колеса и шестерни

Делительные диаметры

d1=m×z1/cosb,                                                                                     (27)

d2=m×z2/cosb,

 где d1 – диаметр шестерни, мм;

d2 – диаметр колеса, мм.

d1=1,5×39/cos11,48°=59,7 мм

d2=1,5×157/cos11,48°=240,3 мм.

Диаметры вершин зубьев

da1=d1+2×m,                                                                                     (28)

da2=d2+2×m,

где da1 – диаметр вершины зуба шестерни, мм;

da2 – диаметр вершины зуба колеса, мм.

da1=59,7+2×1,5= 62,7 мм

da2=240,3+2×1,5= 243,3 мм

Диаметры впадин зубьев

df1= d1-2,5×m,                                                                                      (29)

df2= d2-2,5×m,

 где df1 – диаметр впадины зуба шестерни, мм;

df2 – диаметр впадины зуба шестерни, мм.

df1=59,7 – 2,5×1,5= 55,95мм

df2=240,3 – 2,5×1,5= 236,55 мм

3.1.10. Проверка зубьев шестерни и колеса на контактную выносливость

,                                                   (30)

где К – вспомогательный коэффициент, для косозубых передач К=376 [4,с.61]

Кнα – коэффициент учитывающий распределение нагрузки между зубьями, по графику [4,с.63] находим Кнα = 1,14;

Kнυ – коэффициент, учитывающий динамическую нагрузку, определим по таблице 4.3. [4,с.62] Kнυ = 1,04;

Колесо и шестерня проходят проверку на контактную выносливость.

3.1.11. Проверка зубьев шестерни и колеса на выносливость при изгибе.

sF2=YF2×Yb× KFb×KFn×2×Т2/(d2b2×m)£[sF]2,                                            (31)

sF1=sF2(Y F1/YF2) £[sF]1,                                                                    (32)

где sF1,2 – фактические напряжения изгиба для шестерни и колеса, Н/мм2;

YF1,2 – коэффициенты формы зуба для колеса и шестерни, определяются в зависимости от эквивалентного числа зубьев (zv1=z1/cos3b1 ; zv2=z2/cos3b2), и коэффициента смещения равный 0, и определяется по графику;

Yb - коэффициент, учитывающий наклон зуба;

KFb - коэффициент неравномерности нагрузки по длине зуба,

KFb =1;

KFn - коэффициент, учитывающий динамическую нагрузку, KFn=1,11.

Значение YF1,2 определяем по таблице 4.4 [4,с.64] в зависимости от эквивалентного числа зубьев, zv1,2= z1,2/cos3β.

zv2=157/cos311,48°= 166,8

Страницы: 1, 2, 3, 4