Курсовая работа: Проектирование привода пресс-автомата с плавающим ползуном

Характеристики подшипника качения № 7308 взяты из справочника [4].

  

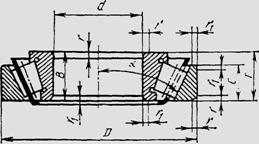
Рисунок 14. Схема конического подшипника качения.

Формула для определения диаметра делительной окружности колеса d1 имеет вид:

d1=z2 , (15)

где m – нормальный модуль зубчатого зацепления;

β – угол наклона линии зуба;

z2 – число зубьев колеса;

d1=1,5·100/cos16˚15΄37˝=150/0,96=156,25 (мм);

Окружную силу определим по формуле:

Ft=2·М∑max/d1, (16)

где М∑max – максимальный момент на тихоходном валу;

dк=d1 – диаметр начальной окружности;

Ft=2·216/156,25·10-3=432/156,25·10-3=2764,8 Н .

Осевую составляющую Fa определим по формуле:

Fa=Ft·tgβ , (17)

Fa=2764,8·tg16˚15΄37˝=805,87 Н.

Радиальную силу определим по формуле:

Fr=(Ft·tgαw)/cosβ , (18)

где αw – угол зацепления косозубой передачи в нормальном сечении (αw≈20˚);

Fr==1048,032 Н .

РАСЧЁТ ТИХОХОДНОГО ВАЛА НА ПРОЧНОСТЬ

Расчёт состоит из нескольких этапов:

1. формирование расчётной схемы вала;

2. расчёт вала на статическую прочность;

3. проектировочный расчёт шпоночного или шлицевого соединения;

4. расчёт вала на выносливость.

Валы в редукторах выполняют ступенчатыми, т.к. это обеспечивает удобный монтаж, надёжную фиксацию подшипников и зубчатых колёс.

Расчёт проводится для тихоходного вала, как наиболее нагруженного.

ФОРМИРОВАНИЕ РАСЧЁТНОЙ СХЕМЫ ВАЛА

Будем считать, что сила, действующая со стороны ролика, на беговую дорожку внутреннего кольца подшипника, приложена в геометрическом центре конического ролика.

Будем полагать, что геометрический центр ролика определяется в осевом направлении размером С/2 и лежит на окружности диаметром

dср===65 (мм).

В качестве прототипа был взят чертёж тихоходного вала мотор-редуктора МЦ-80 (Лист 38) из каталога [3].

Формирование расчётной схемы тихоходного вала показано на Рисунке 16.

При установке радиально-упорных конических подшипников враспор наблюдается смещение опор на расчётной схеме внутрь относительно тел качения на величину 1.

Определим S – смещение опоры относительно середины наружного кольца подшипника:

S===·tg12˚=6,91 (мм).

Определим L=2T+tk+a+b , - расстояние между внешними торцами подшипников,

где T – габаритная ширина подшипника;

tk – ширина венца зубчатого колеса;

a – ширина упорного буртика;

b – размер ступенчатой части колеса.

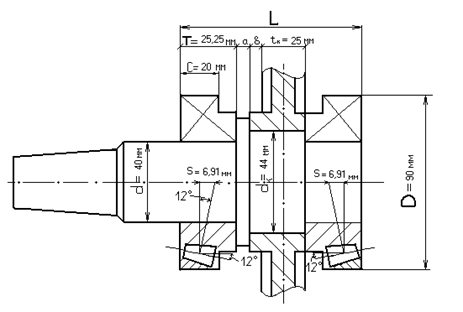
Формирование расчётной схемы вала.

Размеры a и b получены масштабированием сборочного чертежа мотор-редуктора МЦ-80 – [3] и исходя из рекомендаций по выбору данных размеров.

a=6 , b=8

Тогда получим:

L=2·25,25+25+6+8=89,5 (мм).

Определим расчётную длину вала lрас по формуле:

 

lрас=L-2·(+1)=89,5-2·()=67,5 (мм);

где с – ширина наружного кольца подшипника.

Найдём длину lk2, которая определяет положение срединной плоскости колеса:

 

lk2=(Т+tk/2)-(+1)=(25,25+25/2)-()=26,75 (мм).

Зная lk2 , определим размер lk1:

 

lk1=lрас-lk2=67,5-26,75=40,75 (мм).

РАСЧЁТ ВАЛА НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ

Заменим шарнирные опоры силами реакции, а силы, действующие в зубчатом зацеплении, приведём к оси вала:

Ma=Fa·dw/2=Ft·tgβ·dw/2=(2·М∑max/dw)·tgβ·dw/2=М∑max·tgβ=216·0,292=62,96(Н·м);

Mt=Ft·dw/2=(2·М∑max/dw)·dw/2=М∑max=216 (Н·м);

Разложим реакции опор Ra и Rc на составляющие по осям, и найдём их.

1. Составляющие по оси X:

∑Mcy=-xa·lрас+Ft·lk2=0;

 xa=( Ft·lk2)/lрас=(2764,8·26,75·10-3)/67,5·10-3=1095,68 Н;

∑May= xc·lрас-Ft·lk1=0;

 xc=( Ft·lk1)/lрас=(2764,8·40,75·10-3)/67,5·10-3=1669,12 Н;

2. Составляющие по оси Y:

∑Mcx=-ya·lрас+Ma+Fr·lk2=0;

 ya=(Ma+Fr·lk2)/lрас=(62,96+1048,032·26,75·10-3)/67,5·10-3=1348,07 Н;

∑Max=yc·lрас+Ma-Fr·lk1=0;

 yc=(-Ma+Fr·lk1)/lрас=(-62,96+1048,032·40,75·10-3)/67,5·10-3=-300,04 Н;

3. Составляющие по оси Z:

∑Fz=Fa-zc=0; zc=Fa=805,87 Н.

Допущения:

1) пренебрежём влиянием на прочность касательных напряжений от поперечной силы.

2) не учитываем циклический характер нагружения вала, а также влияние на прочность конструктивных (концентрация напряжения) и технологических факторов.

Расчётная схема вала показана на Рисунке 17.

По эпюрам внутренних силовых факторов видно, что опасным сечением является сечение B (под срединной плоскостью колеса (слева)).

В точке Е реализуется плоское упрощенное напряжённое состояние. Для определения эквивалентного напряжения в точке Е воспользуемся третьей теорией прочности.

Запишем условие прочности:

σЕэкв=[σ], для стали 40Х [σ]=80 МПа; (*)

σІІІэкв=σ1-σ3=((σ/2)+√(σ/2)2+τ2)-((σ/2)-√(σ/2)2+τ2)=√σ2+4τ2 .

Для нашего случая воспользуемся частной формулой для определения σэкв:

σЕэкв=·√M2изг+M2∑max .

Подставим данное выражение для σЕэкв в условие прочности и выразим параметр d:

·√M2изг+M2∑max ≤[σ];

 d3≥(32·√M2изг+M2∑max)/[σ]·π; d≥ √(32·√M2изг+M2∑max)/[σ]·π ;

[d]=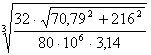==3,07·10-2 (м) = 30,7 (мм).

По ГОСТ 6636-69 «Нормальные линейные размеры» выбираем размер [d]ГОСТ=31 мм.

Тогда d=max(dкат ;[d]ГОСТ)=max(0,044 ; 0,031)=0,044 (м) =44 (мм).

ПРОЕКТИРОВОЧНЫЙ РАСЧЁТ ШПОНОЧНОГО СОЕДИНЕНИЯ

Таблица 7. Размеры шпонки по ГОСТ 23360-78.

Диаметр вала d, мм	Ширина шпонки b, мм	Высота шпонки h, мм	Глубина паза вала t1, мм
44	12	8	5,0

Расчёт шпоночного соединения проводим по напряжениям смятия σсм:

σсм ≤ [σсм] (19)

Для стали 45, из которой чаще всего изготавливают шпонки [σсм]=180 МПа, но так как характер нагрузки – сильные толчки, то это напряжение необходимо понизить на 35%. В результате получим [σсм]=117 МПа.

σсм = Nсм/Sсм ,

где Nсм – сила смятия; Sсм – площадь смятия.

Sсм=(h-t1)·lраб , lраб=l-b , Sсм=(h-t1)·(l-b).

Nсм определим из условия равновесия:

∑Mz=M∑max-Nсм·d/2=0 , Nсм=2· M∑max/d .

Подставим полученные выражения для Sсм и Nсм в условие прочности (19):

2· M∑max/d·(h-t1)·(l-b) ≤ [σсм] . (20)

Из полученного равенства (20) выразим l:

l ≥ (2· M∑max/[σсм]·d·(h-t1))+b;

[l]==0,04 (м) = 40 (мм).

Т.к. длина шпонки [l]=40 (мм) получилась больше, чем длина ступицы Lст=33 (мм) (Lст=tk+b=25+8=33 (мм)), то одна шпонка не удовлетворяет условию прочности. Исходя из этого, необходимо поставить две диаметрально расположенные шпонки. В этом случае длина шпонки будет определяться неравенством:

 

l ≥ (M∑max/[σсм]·d·(h-t1))+b;

[l]==0,026 (м) = 26 (мм).

Согласно ГОСТ 23360-78 длину шпонки выбираем l=28 (мм).

Lст-l =33-28=5 (мм),

что удовлетворяет условию выбора шпонок: Lст-l =5…15 (мм).

По результатам проектировочного расчёта шпоночного соединения назначим две диаметрально расположенные шпонки 12×8×28 по ГОСТ 23360-78.

РАСЧЁТ ВАЛА НА ВЫНОСЛИВОСТЬ

Все расчётные зависимости и значения коэффициентов взяты из учебника [5].

Проверочный расчёт вала на выносливость выполним с учётом формы циклов нормального и касательного напряжений, конструктивных и технологических факторов. Проверочный расчёт заключается в определении расчётного фактического коэффициента запаса прочности и сравнении его со значением нормативного коэффициента.

n ≥ [n] ,

где [n]=2,5 – значение нормативного коэффициента запаса прочности.

Значение n найдём по формуле:

n=, (21)

где nσ – фактический коэффициент запаса прочности по нормальным напряжениям;

nτ – фактический коэффициент запаса прочности по касательным напряжениям.

Величину nσ определим по формуле:

nσ=σ-1/[(kσ·β·σa/εσ)+σm·ψσ] , (22)

где σ-1=410 МПа для стали 40Х (термообработка улучшение) – предел выносливости стали при симметричном изгибе;

kσ=1,77 – (для канавки, полученной пальцевой фрезой) – эффективный коэффициент концентрации нормальных напряжений при изгибе;

β=1,2 – коэффициент, отражающий влияние качества обработки поверхности вала (вид обработки – точение);

εσ=0,81 – коэффициент масштабного фактора (соответствует диаметру вала равному 44 мм);

ψσ=0,1 – коэффициент, отражающий влияние асимметрии цикла на усталостную прочность;

σa – амплитуда цикла нормальных напряжений при изгибе;

σm – среднее напряжение цикла при изгибе.

При определении параметров цикла (σm и σa) будем использовать следующие допущения:

1) максимальные и минимальные напряжения реализуются в одной и той же опасной точке, положение которой было определено ранее (пункт 7.2);

2) будем считать, что изгибающий момент в сечении изменяется пропорционально крутящему моменту.

Значения σa вычисляется по формуле:

σa=(σmax-σmin)/2 .

Значения σm вычисляется по формуле:

σm=(σmax+σmin)/2 .

Найдём величину σmax по формуле:

σmax =Mmaxизг / Wx ,

где Mmaxизг=70,79 Н·м;

Wx=0,1·d3-b·t1·(d-t1)2/d –

момент сопротивления сечения вала с двумя шпоночными канавками.

Wx=0,1·(44·10-3)3 - =6,44·10-6 (м3);

σmax ==11·106 (Па).

Из графика зависимости нормальных напряжений от угла поворота вала (Рисунок 21) видно, что минимальные нормальные напряжения σmin действуют, когда вал находится в 9 положении.

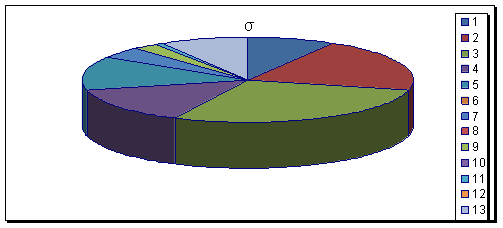
Схема к определению нормальных напряжений и график зависимости нормальных напряжений от угла поворота вала.

Величину σmin вычислим по формуле:

|σmin|=|M∑(9)/M∑max|·σmax·|y(9)/ymax|=·11·106·sin90˚=1,012·106 (Па).

В результате расчётов получим, что

σmax= σ3=11 МПа и σmin= σ9=-1,012 МПа.

σа=(σmax -σmin)/2==6,006 МПа;

σm=(σmax +σmin)/2==4,994 МПа.

Определим значение коэффициента запаса прочности по нормальным напряжениям nσ по формуле (22):

nσ=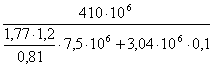=20,53.

Значение nτ определяется по формуле:

nτ= τ-1/[(kτ·β·τa/ετ)+τm·ψτ] , (23)

где τ-1=240 МПа для стали 40Х – предел выносливости стали при симметричном кручении; kτ=2,22 – эффективный коэффициент концентрации напряжений при кручении;

β=1,2 – коэффициент, отражающий влияние качества обработки поверхности вала;

ετ=0,75 – коэффициент масштабного фактора;

ψτ=0,05 – коэффициент, отражающий влияние асимметрии цикла на усталостную прочность вала;

τa – амплитуда цикла касательных напряжений при кручении;

τm – среднее напряжение цикла при кручении.

Закон распределения касательных напряжений τ(φ) совпадает с законом изменения суммарного момента M∑(φ).

Вычислим значение τmax по формуле:

τmax =M∑max / Wx ,

где M∑max=216 Н·м;

Wx=0,2·d3-b·t1·(d-t1)2/d=0,2·(44·10-3)3 - =

=14,96·10-6 (м3);

τmax ==14,44·106 (Па).

Аналогично вычислим τmin:

 τmin=M∑min / Wx== -7,17·106 (Па).

Зная τmax и τmin, определим значения τa и τm:

τa=(τmax -τmin)/2==10,81·106 (Па);

τm=(τmax +τmin)/2==3,64·106 (Па).

График зависимости касательных напряжений от угла поворота вала.

Вычислим коэффициент запаса прочности nτ по формуле (23):

nτ=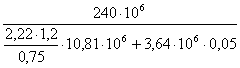=6,221.

Найдём значение расчётного коэффициента запаса прочности по формуле (21):

n==5,95.

Расчётное значение фактического коэффициента запаса прочности получилось больше значения нормативного коэффициента запаса прочности: n ≥ [n], 5,95 > 2,5 - это удовлетворяет расчёту вала на выносливость.

ПРОВЕРОЧНЫЙ РАСЧЁТ ЗУБЧАТОЙ ПАРЫ НА ПРОЧНОСТЬ

Все используемые в этом разделе формулы и расчётные зависимости взяты из конспекта лекций [2].

ОПРЕДЕЛЕНИЕ РЕСУРСА ПЕРЕДАЧИ

Ресурс передачи вычислим по формуле:

Lп=365·Г·Кг·8·C·Кс ,

где Г=7 – количество лет службы передачи;

Кг===0,658 –

коэффициент годового использования;

С=2 – количество смен;

8 – продолжительность рабочей смены в часах;

Кс===0,875 –

коэффициент сменного использования.

В результате получим:

Lп=365·7·0,658·2·8·0,875=23536,66 (часов).

Шестерню изготавливают более твёрдой (твёрдость поверхности зубьев определяется термообработкой), т.к. число её зубьев меньше, чем у колеса, поэтому она совершает большее число оборотов и испытывает большее число циклов нагружения.

Следовательно, для равномерного изнашивания зубъев передачи твёрдость материала шестерни должна быть выше твёрдости материала колеса на 3…5 единиц по шкале Раквелла.

Характеристики материала колеса и шестерни приведены в Таблице 8.

Таблица 8. Характеристики материала зубчатой пары

Элемент зубчатого зацепления	марка стали	твёрдость HRC	технология упрочнения
колесо	40Х	50	поверхностная закалка
шестерня	40Х	54	поверхностная закалка

РАСЧЁТ ПОВЕРХНОСТИ ЗУБА КОЛЕСА НА ПРОЧНОСТЬ ПО КОНТАКТНЫМ НАПРЯЖЕНИЯМ

Расчёт проводим для колеса, как наиболее слабого элемента зацепления.

Запишем условие прочности:

σн ≤ [σн] ,

где σн – действующее напряжение при циклическом контактном воздействии;

[σн] – допускаемое контактное напряжение.

Значение допускаемого контактного напряжения [σн] определяется по формуле:

[σн]=(σно·kHL)/[kH] , (24)

где σно – предел контактной выносливости при базовом числе циклов нагружения (зависит от материала и термообработки);

σно=17·HRC+200=17·50+200=1050 МПа;

kHL – коэффициент долговечности;

kHL= ,

где NHO=4·106 – базовое число циклов нагружения (взято из конспекта лекций [2]).

NHE=60·c· n1·Lп , - число циклов за весь период эксплуатации;

где c=1 – число вхождений зуба в зацепление за один оборот;

NHE=60·140·23536,66=197,71·106 ;

kHL=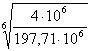=0,522 ,

т.к. у нас термообработка поверхности зубьев - поверхностная закалка, то 1 ≤ kHL ≤ 1,8 и, следовательно, берём kHL=1.

[kH]=1,25 – коэффициент безопасности (выбирается в зависимости от вида термохимической обработки зубьев: поверхностная закалка).

Вычислим значение [σн] по формуле (24):

[σн]=·1=840·106 Па.

Значение σн вычислим по формуле:

σн=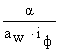· 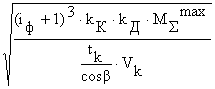, (25)

где α=340000 Н·м2 – вспомогательный коэффициент, который зависит от материала колеса и шестерни (сталь – сталь);

kД – коэффициент динамичности, отражающий неравномерность работы зубчатой передачи (зависит от скорости и точности передачи);

kК – коэффициент концентрации, отражающий неравномерность распределения напряжений по длине линии контакта;

kД ·kК =1,3 ;

Vк=1,35 – коэффициент, отражающий повышенную нагрузочную способность косозубых и шевронных колёс;

aw=100·10-3 м – межосевое расстояние;

iф=3,57 – передаточное число редуктора;

tk=25·10-3 м – ширина венца зубчатого колеса;

β=16˚15΄37˝ - угол наклона линии зуба;

M∑max=216 (Н·м) – максимальный суммарный момент.

Следовательно, σн по формуле (25) получится:

σн=·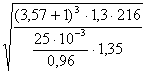=831,54·106 Па.

Как видно из расчёта, условие прочности по контактным напряжениям выполняется: 831,54•106 < 840·106. Следовательно, вид термохимической обработки зубьев выбран верно.

РАСЧЁТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННОМ ИЗГИБЕ

Запишем условие прочности:

σF ≤ [σF] ,

где σF - действующее напряжение при переменном изгибе;

[σF] – допускаемое напряжение при переменном изгибе.

Значение [σF] определим по формуле:

[σF]=·kFL , (26)

где σ-1F = 700 МПа – предел выносливости материала при симметричном изгибе; [kF]=1,75 – коэффициент безопасности (зависит от технологии изготовления зубчатого колеса: заготовка получается штамповкой); kFL – коэффициент долговечности;

kFL= ,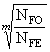

где NFO=4·106 – базовое число циклов нагружения (взято из конспекта лекций [2]);

NFЕ = NHE =197,71·106 – число нагружений зуба колеса за весь срок службы передачи;

m=9, т.к. HB>350.

kFL==0,648.

Т.к. 1 ≤ kFL ≤ 1,63 ,то принимаем kFL = 1.

Вычислим значение [σF] по формуле (26):

[σF]=·1=400·106 Па.

Величину σF определим по формуле:

σF =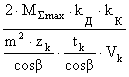 ·YF , (27)

где M∑max=216 (Н·м) – максимальный суммарный момент;

kД ·kК =1,3 , где kК – коэффициент концентрации, kД – коэффициент динамичности;

m=1,25·10-3 м – нормальный модуль зубчатого зацепления;

tk=25·10-3 м – ширина венца зубчатого колеса;

β=16˚15΄37˝ - угол наклона линии зуба;

zk = z2 = 100 - число зубьев колеса;

Vк=1,35 – коэффициент формы зуба.

YF выбираем по эквивалентному числу зубьев zv, где

zv===113.

Соответственно YF = 3,75.

Найдём величину σF по формуле (27):

σF = 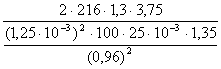==368,05 МПа.

Получили, что 368,05 МПа < 400 МПа , а это удовлетворяет условию σF ≤ [σF].

 

ЗАКЛЮЧЕНИЕ

По заданным геометрическим, весовым и эксплуатационным параметрам был выполнен синтез плоского рычажного механизма с одной степенью свободы, в результате которого были найдены размеры звеньев механизма и межопорные расстояния.

Был произведен кинематический анализ механизма, основанный на построении ряда последовательных положений звеньев механизма и соответствующих им планов скоростей, в результате которого были определены относительные линейные скорости характерных точек и относительные угловые скорости звеньев.

Далее был проведен силовой анализ механизма. С целью его упрощения были заменены все звенья и усилия эквивалентной с точки зрения нагруженности привода динамической моделью. На основе динамического анализа были определены составляющие момента движущих сил (Мдв), предназначенные для преодоления сил статистического сопротивления – статический момент (Мст), и динамического сопротивления – динамический момент (Мдин). При определении суммарного момента движущих сил (М∑) были учтены потери на трение (КПД механизма равен 68%).

На основе расчетного момента Мрасч (Мрасч=k1·k2·Мн=222,32 Н·м, где величина Мн – есть среднеинтегральное значение функции М∑(φ), К1 – коэффициент, отражающий повышенную частоту вращения быстроходного вала редуктора, К2 – коэффициент, отражающий влияние характера нагрузки) был выбран цилиндрический одноступенчатый мотор-редуктор МЦ-100 с максимальным крутящим моментом на выходном валу Т=230 Н·м передаточным числом i=3,57 и коническими радиальноупорными подшипниками №7308 на тихоходном валу, установленными враспор.

Для тихоходного вала редуктора, который выполнен из стали 40Х (термическая обработка – улучшение), в результате проектировочного расчёта на статическую прочность был определён диаметр вала (d=44 мм) в опасном сечении – под срединной плоскостью зубчатого колеса. По результатам проектировочного расчёта на прочность при смятии для соединения «вал – колесо» были выбраны две диаметрально расположенные призматические шпонки 12×8×28 со скруглёнными краями по ГОСТ 23360-78.

Далее был произведён проверочный расчёт вала на выносливость с учётом конструктивных и технологических факторов, а также форм циклов нормальных и касательных напряжений, в результате которого было установлено, что вал удовлетворяет условию усталостной прочности, т.к. значение фактического коэффициента запаса прочности n=5,95 больше, чем значение нормативного коэффициента [n]=2,5.

Проверочный расчёт зубчатой пары на прочность (в качестве материала колеса и шестерни была выбрана сталь 40Х с поверхностной закалкой рабочей поверхности зубьев) по контактным и изгибающим напряжениям подтвердил работоспособность зубчатой пары (действующее контактное напряжение σн примерно равно допускаемому напряжению [σн], действующее напряжение при переменном изгибе σF примерно равно допускаемому напряжению [σF]).

Следовательно, можно сказать, что спроектированный привод пресс-автомата удовлетворяет всем условиям работоспособности, рассмотренным в расчётно-пояснительной записке.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Порошин В.Б., Худяков А.В. Проектирование привода механического оборудования. : Учебное пособие по курсовому проектированию – Челябинск: ЮУрГУ, 1997 – 38с.

2. Порошин В.Б., Ребяков Ю.Н., Деккер В.В. Конспект лекций по прикладной механике. – Челябинск: ЮУрГУ, 2003. – 210 с. (На правах рукописи).

3. Анфимов М.И. Редукторы. Конструкции и их расчёт. : Альбом. – М.: Машиностроение, 1993 – 464с.

4. Перель Л.Я. Подшипники качения: Расчёт, проектирование и обслуживание опор: Справочник. – М.: Машиностроение, 1983. – 543с.

5. Иосилевич Г.Б., Лебедев П.А., Стреляев В.С. Прикладная механика. – М.: Машиностроение, 1985. -576с.

6. Гузенков П.Г. Детали машин: учебное пособие для втузов – М. : 1982. – 351с.