Курсовая работа: Проектирование привода пресс-автомата с плавающим ползуном

Проведём расчёт Iпр для всех выбранных положений механизма по формуле (9):

Iпр1=336,7·(0,025)²+7,653·(0,083)²+2,251·(0)²+102·(0)²=0,21+0,053=0,263 (кг·м²);

Iпр2=336,7·(0,032)²+7,653·(0,082)²+2,251·(0,115)²+102·(0,025)²=0,345+0,052+0,030+ +0,064=0,491 (кг·м²);

Iпр3=336,7·(0,046)²+7,653·(0,05)²+2,251·(0,22)²+102·(0,044)²=0,712+0,019+0,109+ +0,197=1,037 (кг·м²);

Iпр4=336,7·(0,05)²+7,653·(0)²+2,251·(0,238)²+102·(0,05)²=0,842+0+0,128+0,255=1,225 (кг·м²);

Iпр5=336,7·(0,043)²+7,653·(0,051)²+2,251·(0,193)²+102·(0,042)²=0,623+0,02+0,084+ +0,180=0,907 (кг·м²);

Iпр6=336,7·(0,031)²+7,653·(0,079)²+2,251·(0,107)²+102·(0,024)²=0,324+0,048+0,026+ +0,059=0,457 (кг·м²);

Iпр7=336,7·(0,025)²+7,653·(0,083)²+2,251·(0)²+102·(0)²=0,210+0,053+0+0=0,263 (кг·м²);

Iпр8=336,7·(0,037)²+7,653·(0,068)²+2,251·(0,129)²+102·(0,028)²=0,461+0,035+0,037+ +0,08=0,613 (кг·м²);

Iпр9=336,7·(0,045)²+7,653·(0,035)²+2,251·(0,197)²+102·(0,042)²=0,682+0,01+0,087+ +0,18=0,959 (кг·м²);

Iпр10=336,7·(0,05)²+7,653·(0)²+2,251·(0,238)²+102·(0,05)²=0,842+0+0,126+0,255=1,223 (кг·м²);

Iпр11=336,7·(0,046)²+7,653·(0,035)²+2,251·(0,21)²+102·(0,043)²=0,712+0,01+0,099+ +0,189=1,01 (кг·м²);

Iпр12=336,7·(0,036)²+7,653·(0,062)²+2,251·(0,133)²+102·(0,027)²=0,436+0,029+0,04+ +0,074=0,579 (кг·м²);

Значение первой производной приведённого момента инерции по углу поворота кривошипа определим, используя аппроксимацию первой производной конечными разностями:

I´прi=(dIпрi/dφi)=(Iпр(i+1) -Iпрi)/(φ(i+1) -φi) , (10)

где Iпр(i+1), Iпрi – значения приведённого момента инерции для i+1 и i-го положений кривошипа, соответственно;

φ(i+1) и φi – значения угла поворота кривошипа для i+1 и i-го положений кривошипа, соответственно.

Для вычисления первой производной I´пр(φ) по формуле (10) необходимо дополнительно разбить график Iпр(φ) на интервалы, т.к. стандартных двенадцати положений явно недостаточно.

В положениях 8, 15, 22 функция Iпр(φ) имеет экстремумы, поэтому первая производная I´пр(φ) в этих точках равна нулю. Проведём расчёт I´пр(φ) по формуле (10):

I´пр1=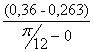==0,371 (кг·м²/рад);

I´пр2=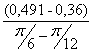==0,5 (кг·м²/рад);

I´пр3=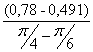==1,104 (кг·м²/рад);

I´пр4=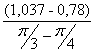==0,982 (кг·м²/рад);

I´пр5=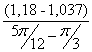==0,546 (кг·м²/рад);

I´пр6=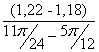==0,306 (кг·м²/рад);

I´пр7=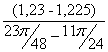==0,076 (кг·м²/рад);

I´пр8=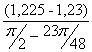==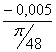-0,076 (кг·м²/рад);

I´пр9=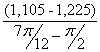==-0,458 (кг·м²/рад);

I´пр10=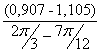==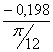-0,756 (кг·м²/рад);

I´пр11=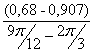==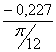-0,867 (кг·м²/рад);

I´пр12=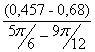==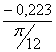-0,852 (кг·м²/рад);

I´пр13=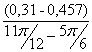==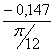-0,562 (кг·м²/рад);

I´пр14=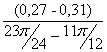==-0,31 (кг·м²/рад);

I´пр15=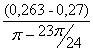==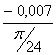-0,054 (кг·м²/рад);

I´пр16=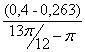==0,523 (кг·м²/рад);

I´пр17=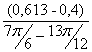==0,814 (кг·м²/рад);

I´пр18=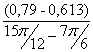==0,676 (кг·м²/рад);

I´пр19=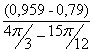==0,646 (кг·м²/рад);

I´пр20=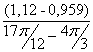==0,615 (кг·м²/рад);

I´пр21=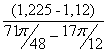==0,535 (кг·м²/рад);

I´пр22=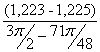==-0,008 (кг·м²/рад);

I´пр23=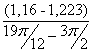==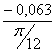-0,241 (кг·м²/рад);

I´пр24=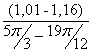==-0,573 (кг·м²/рад);

I´пр25=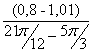==-0,802 (кг·м²/рад);

I´пр26=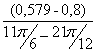==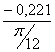-0,844 (кг·м²/рад);

I´пр27=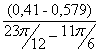==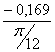-0,646 (кг·м²/рад);

По результатам вычислений I´пр(φ) строим график зависимости первой производной Iпр от угла поворота кривошипа. Значения I´пр(φ) в выбранных положениях (в таблицу занесены только основные положения) приведены в Таблице 4. Экстремумы функции в точках 8, 22 смещены в положения 4, 10, соответственно.

По формуле 6 рассчитаем момент движущих сил для преодоления сил динамического сопротивления во всех выбранных положениях механизма:

Мдин=107,3113·dIпр/dφ ;

Мдин1=107,3113·0=0 (н·м);

Мдин2=107,3113·0,5=53,656 (н·м);

Мдин3=107,3113·0,982=105,38 (н·м);

Мдин4=107,3113·(-0,08)=-8,585 (н·м);

Мдин5=107,3113·(-0,76)=-81,557 (н·м);

Мдин6=107,3113·(-0,85)=-91,215 (н·м);

Мдин7=107,3113·(-0,05)=-5,366 (н·м);

Мдин8=107,3113·0,814=87,351 (н·м);

Мдин9=107,3113·0,646=69,323 (н·м);

Мдин10=107,3113·(-0,01)=-1,073 (н·м);

Мдин11=107,3113·(-0,57)=-61,167 (н·м);

Мдин12=107,3113·(-0,84)=-90,142 (н·м).

Полученные значения Мдин приведены в Таблице 4.

График зависимости Мдин(φ) показан на Рисунке 13.

Рисунок 12. Зависимости приведённого момента инерции Iпр и его первой производной I´пр от угла поворота кривошипа.

РАСЧЁТ КПД МЕХАНИЗМА

Момент движущих сил Мдв, в соответствии с зависимостью (1), был определён в предположении, что кинематические пары механизма идеальны.

Влияние сил трения учитывают с помощью коэффициента полезного действия η. При последовательном соединении кинематических пар их общий КПД определяется следующим выражением:

η=η1·η2·……·ηк , где к-число кинематических пар.

При параллельном соединении кинематических пар КПД определяется как среднее арифметическое КПД отдельных пар, при условии, что поток мощности распределяется равномерно между кинематическими парами:

η=(η1+η2+…+ηк)/к , где к-число кинематических пар.

Суммарный КПД для нашего механизма (Рисунок 14) равен:

η∑= [(ηс+ηс)/2]·ηс·ηк·ηпн2·ηпн4·ηк·[(ηс+ηс)/2]= ηс·ηс·ηк·ηпн2·ηпн4·ηк·ηс=

= η3с· η2к·ηпн2·ηпн4 , (11)

где ηс=0,98 – КПД подшипника скольжения;

ηк=0,99 – КПД подшипника качения;

ηпн2=0,86 – КПД кинематической пары «ползун по направляющей»;

ηпн4=0,86 – КПД кинематической пары «пуансон по направляющей»;

Т.к. сила, определяющая в направляющих потери на трение, была учтена явным образом при подсчёте статического момента, то в формулу вычисления КПД она не входит.

η∑=(0,98)3·(0,99)2·0,86·0,86=0,68.

РАСЧЁТ ДВИЖУЩЕГО МОМЕНТА М∑(Φ)

По формуле (1) мы определяем момент движущих сил, считая, что кинематические пары идеальны. Однако силы трения присутствуют всегда, и их обычно учитывают с помощью коэффициента полезного действия – КПД.

Выражение для суммарного момента движущих сил М∑ с учётом потерь на трение примет вид:

М∑=k·(Мст+Мдин) , (12)

где k – коэффициент, учитывающий присутствие сил трения в кинематических парах, равный: k=η , если (Мдв<0) – соответствуетработе привода в режиме генератора (когда привод играет роль тормоза);

k=1/η , если (Мдв>0) – соответствует работе привода в режиме двигателя.

Используя данные Таблицы 4, рассчитаем суммарный момент движущих сил М∑ для всех выбранных положений механизма:

М∑1=Мдв1/η=82,5/0,68=121,32 (н·м);

М∑2=Мдв2/η=115,2/0,68=169,41 (н·м);

М∑3=Мдв3/η=138,8/0,68=204,12 (н·м);

М∑4=Мдв4/η=78,91/0,68=116,04 (н·м);

М∑5=Мдв5/η=123,6/0,68=181,76 (н·м);

М∑6=Мдв6·η=-151·0,68=-102,68 (н·м);

М∑7=Мдв7·η=-87,9·0,68=-59,77 (н·м);

М∑8=Мдв8·η=-1,85·0,68=-1,26 (н·м);

М∑9=Мдв9/η=12,92/0,68=19 (н·м);

М∑10=Мдв10·η=-1,07·0,68=-0,73 (н·м);

М∑11=Мдв11·η=-13,3·0,68=-9,04 (н·м);

М∑12=Мдв12·η=-14,6·0,68=-9,93 (н·м);

М∑13=Мдв13/η=82,5/0,68=121,32 (н·м);

Полученные данные приведены в Таблице 4.

Зависимость М∑(φ) представлена на Рисунке 13.

Таблица 4. Результаты расчёта момента движущих сил и его составляющих.

№ положения	1	2	3	4	5	6	7	8	9	10	11	12	1
φ, рад	0	π/6	π/3	π/2	2π/3	5π/6	π	7π/6	4π/3	3π/2	5π/3	11π/6	2π
Мст, н•м	82,5	61,58	33,41	87,5	205,2	-59,6	-82,5	-89,2	-56,4	0	47,9	75,48	82,5
Q , кН	0	0	0	1,75	5,54	0	0	0	0	0	0	0	0
Iпр, кг•м²	0,263	0,491	1,037	1,225	0,907	0,457	0,263	0,613	0,959	1,223	1,01	0,579	0,263
I´пр, кг•м²/рад	0	0,5	0,982	-0,08	-0,76	-0,85	-0,05	0,814	0,646	-0,01	-0,57	-0,84	0
Мдин, н•м	0	53,66	105,4	-8,59	-81,6	-91,2	-5,37	87,35	69,32	-1,07	-61,2	-90,1	0
Мдв, н•м	82,5	115,2	138,8	78,91	123,6	-151	-87,9	-1,85	12,92	-1,07	-13,3	-14,6	82,5
М∑, н•м	121,3	169,4	204,1	116	181,8	-103	-59,8	-1,26	19	-0,73	-9,04	-9,93	121,3

Страницы: 1, 2, 3, 4, 5