Курсовая работа: Редуктор двухступенчатый соосный двухпоточный

- радиальная

; где α=20° - угол зацепления; (3.8)

; Н;

Осевые силы в прямозубой передачи отсутствуют.

Все вычисленные параметры заносим в табл.2.

3.2 Проверочный расчет по контактным напряжениям

Проверку контактных напряжений производим по формуле {4, c.64]:

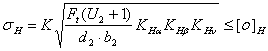; (3.9)

где: - К - вспомогательный коэффициент, для прямозубых передач К=436;

Ft =531Н (табл.2);

U2=5;

КНα – коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых колес КНα =1;

КНβ – см. п.3.1;

КНυ – коэффициент динамической нагруки, зависящий от окружной скорости колес и степени точности передачи, КНυ =1,04 [4, табл.4.3].

(3.10)

Определяем ∆σН

;

; недогрузки, что допускается.

3.3 Проверочный расчет зубьев на изгиб

Расчетные напряжения изгиба в основании ножки зубьев колеса и шестерни [4,с.67]:

; (3.11)

; (3.12)

где: КFβ – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев КFβ =1;

КFv - коэффициент динамической нагруки, зависящий от окружной скорости колес и степени точности передачи, КНυ =1,1 [4, табл.4.3];

YF1 и YF2 – коэффициенты формы зуба шестерни и колеса, YF1 =3,9, YF2 =3,61 [4,табл.4.4].

Подставив значения в формулы (3.11) и (3.12), получим:

;

Прочность зубьев на изгиб обеспечивается.

Определяем ∆σF

;

Все вычисленные параметры проверочных расчетов заносим в табл.3.

Таблица 3 Параметры проверочных расчетов

Параметр	Обозн.	Допускаемое	Расчетное	Недогрузка(-) или перегрузка(+)
Контактное напряжение, МПа	σН	482,7	435	-10%
Напряжение изгиба, МПа	σF1	281	59,4	-79%
Напряжение изгиба, МПа	σF2	257	55	-78%

4 Расчет быстроходной ступени привода

Межосевое расстояние для быстроходной ступени с учетом того, что редуктор соосный и двухпоточный, определяем половину расстояния тихоходной ступени:

а=d2-d1;

а=84-14=70мм.

Из условия (3.2) принимаем модуль mn=1,5мм

Определяем суммарное число зубьев по формуле (3.12) [1,c.36]:

zΣ=2а/mn;

zΣ=2·70/1,5; zΣ=93,3

Принимаем zΣ=94.

Определяем число зубьев шестерни и колеса по формулам (3.13) [2,c.37]:

z1= zΣ/(U1+1); z1=94/(2,5+1); z1=26,1; принимаем z1=26.

Тогда z2= zΣ-z1=94-26=68

Фактическое передаточное соотношение U1=68/26=2,6

Отклонение передаточного числа от номинального незначительное.

Определяем делительные диаметры шестерни и колеса по формуле (3.17) [2,c.37]:

d1=mn·z1=1,5х26=39мм;

d2=mn·z2=1,5х68=102мм;

Определяем остальные геометрические параметры шестерни и колеса по формулам [2,c.37]:

; ;

; ; ;

мм;

; мм;

; мм

; мм;

Определяем окружные скорости колес

; м/с.

Назначаем точность изготовления зубчатых колес – 7А [2,c.32].

Определяем силы в зацеплении (3.7, 3.8):

- окружная

; Н;

- радиальная

; Н.

Осевые силы в прямозубой передачи отсутствуют.

Все вычисленные параметры заносим в табл.4.

Таблица 4 Параметры зубчатой передачи быстроходной ступени

Параметр	Шестерня	Колесо
mn,мм	1,5
ha,мм	1,5
ht,мм	1,875
h,мм	3,375
с, мм	0,375
z	26	68
d,мм	39	102
dа,мм	42	105
df,мм	35,25	98,25
b, мм	22	25
аW,мм	70
v, м/с	1,4
Ft, Н	166,7
Fr, Н	60,7

Учитывая, что геометрические параметры быстроходной ступени незначительно отличаются от тихоходной, выполнение проверочных расчетов нецелесообразно.

5 Проектный расчет валов редуктора

По кинематической схеме привода составляем схему усилий, действующих на валы редуктора по закону равенства действия и противодействия. Для этого мысленно расцепим шестерни и колеса редуктора, при этом дублирующий вал не учитываем.

Схема усилий приведена на рис.1.

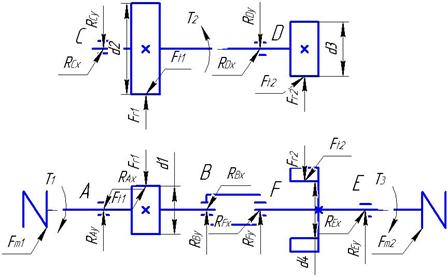
Рис.2 Схема усилий, действующих на валы редуктора.

Из табл.1,2,4 выбираем рассчитанные значения:

Т1=3,4 Нм; Т2=8,5 Нм; Т3=42,5 Нм;

Ft1=166,7 Н; Ft2=1012 Н; Fr1=60,7 Н; Fr2=368 Н;

d1=39мм; d2=102мм; d3=14мм; d4=84мм.

Fm1 и Fm1 – консольные силы от муфт, которые равны [4, табл.6.2]:

; ;

Н; Н.

Rx и Ry – реакции опор, которые необходимо рассчитать.

Так как размеры промежуточного вала определяются размерами остальных валов, расчет начнем с тихоходного вала.

5.1 Расчет тихоходного вала редуктора

Схема усилий действующих на валы редуктора представлена на рис.2.

Назначаем материал вала. Принимаем сталь 40Х, для которой [2, табл.8.4] σв=730Н/мм2; Н/мм2; Н/мм2; Н/мм2.

Определяем диаметр выходного конца вала под полумуфтой из расчёта на чистое кручение [2,c.161]:

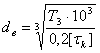
где [τк]=(20…25)МПа

Принимаем [τк]=20МПа.

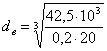; мм.

Принимаем окончательно с учетом стандартного ряда размеров Rа20 (ГОСТ6636-69):

мм.

Намечаем приближенную конструкцию ведомого вала редуктора (рис.3), увеличивая диаметр ступеней вала на 5…6мм, под уплотнение допускается на 2…4мм и под буртик на 10мм.

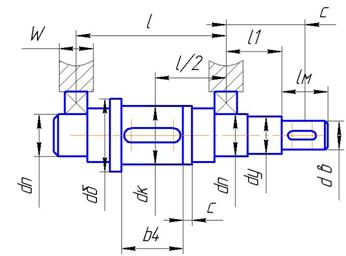
Рис.3 Приближенная конструкция тихоходного вала

мм;

мм – диаметр под уплотнение;

мм – диаметр под подшипник;

мм – диаметр под колесо;

мм – диаметр буртика;

b4=25мм.

Учитывая, что осевых нагрузок на валу нет предварительно назначаем подшипники шариковые радиальные однорядные особо легкой серии по мм подшипник №106, у которого Dп=55мм; Вп=13мм [4,табл.К27].

Выбираем конструктивно остальные размеры:

W=20мм; lм=20мм; l1=35мм; l=60мм; с=5мм.

Определим размеры для расчетов:

l/2=30мм;

с=W/2+ l1+ lм/2=55мм – расстояние от оси полумуфты до оси подшипника.

Проводим расчет тихоходного вала на изгиб с кручением.

Заменяем вал балкой на опорах в местах подшипников (см. рис.4). Назначаем характерные точки 1,2, 3 и 4.

Определяем реакции в подшипниках в вертикальной плоскости.

ΣМ2y=0; RFy·0,06-Fr2·0,03=0

RFy= 368·0,06/ 0,03;

RЕy= RFy=736Н.

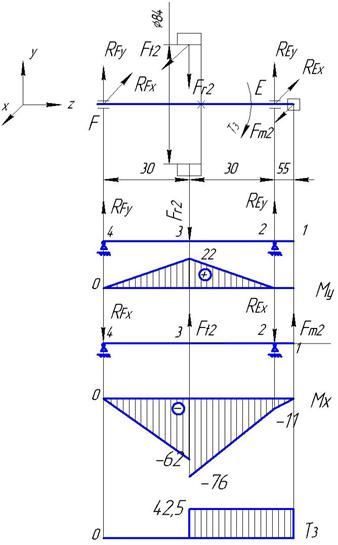
Рис.4 Эпюры изгибающих моментов тихоходного вала

Определяем изгибающие моменты в характерных точках:

М1у=0;

М2у=0;

М3у= RЕy·0,03;

М3у =22Нм2;

М3у=0;

Строим эпюру изгибающих моментов Му, Нм2 (рис.3)

Определяем реакции в подшипниках в горизонтальной плоскости.

ΣМ4x=0; Fm2·0,115- RЕx·0,06+ Ft2·0,03=0;

RЕx=( 814·0,115+ 1012·0,03)/ 0,06;

RЕx=2066Н;

ΣМ2x=0; Fm2·0,055- Ft2·0,03+ RFx·0,6=0;

RFx= (1012·0,03- 814·0,055)/ 0,06;

RFx=-240Н, результат получился отрицательным, следовательно нужно изменить направление реакции.

Определяем изгибающие моменты:

Страницы: 1, 2, 3

МЕНЮ

Курсовая работа: Редуктор двухступенчатый соосный двухпоточный

ИНТЕРЕСНОЕ