Курсовая работа: Привод к лебедке

аW = 61 × 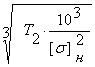, (35)

где Т2 - вращающий момент на валу червячного колеса, Т2 = 231,16 Нм

аW = 61 × 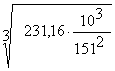= 132,029 мм

Принимаем по ГОСТ аW = 140 мм

Число витков червяка при Uч = 16 (стр.21 [2]) принимаем Z = 2.

Число зубьев червячного колеса Z2, определяем по формуле

Z2 = Z1 × Uч, (36)

Z2 = 2 × 16 = 32

Принимаем Z2 = 32

Модуль зацепления m, мм определяем по формуле

m = (1,4…1,7) × аW / Z2, (37)

m = (1,4…1,7) × 140/32 = (6,56….7,43) мм

Округляем в большую сторону m =7 мм.

Коэффициент диаметра червяка q, определяем по формуле

q = (2 × аW/m) - Z2, (38)

q = (2 × 140/7) - 32 = 8

Принимаем q = 8

Коэффициент смещения инструмента х, определяем по формуле

Х = (аW/ m) - 0,5 × (q + Z2), (39)

Х = (140/4) - 0,5 × (8 + 32) = 0 > - 1, условие не выполняется

Фактическое передаточное число Uф, определяем по формуле

Uф = Z2/Z1,Uф = 32/2 = 16 (40)

Отклонение ΔUф = 100% (Uф - U) / U = 0% < 4%

Фактическое межосевое расстояние аWф, мм определяем по формуле

аWф = 0,5 × m × (q + Z2 + 2 × Х), (41)

аWф = 0,5 × 7 × (8 + 32 + 2 × 0) = 140 мм

Делительный диаметр червяка d1, мм определяем по формуле

d1 = q × m, (42)

d1 = 8 ×7 = 56 мм

Начальный диаметр червяка dW1, мм определяем по формуле

dW1 = m × (q + 2 × Х), (43)

dW1 = 7 × (8 + 2 × 0) =56 мм

Диаметр вершин витков червяка d а1, мм определяем по формуле

d а1 = d1 + 2 × m, (44)

d а1 = 56 + 2 × 7 = 70 мм

Диаметр впадин витков червяка d F1, мм определяем по формуле

d F1 = d1 - 2.4 × m, (45)

d F1 = 56 - 2,4 × 7 = 39,2 мм

Делительный угол подъема линии витков червяка Y, o определяем по формуле

Y = arctg (Z1 /q), (46)

Y = arctg (2/8) =14 o03 /

Длина нарезаемой части червяка b1, мм определяем по формуле

b1 = (10 + 5,5 × |Х| + Z1) × m + С, (47)

где Х = 0, С = 0

b1 = (10 + 5,5 × |0| + 2) × 7 + 0 = 84 мм

Делительный диаметр червячного колеса d2, мм определяем по формуле

d2 = d W 2 = m × Z2, (48)

d2 = d W 2 = 7 × 32 = 224 мм

Диаметр вершин зубьев червячного колеса d а2, мм определяем по формуле

d а2 = d2 + 2 × m × (1 + Х), (49)

d а2 = 224 + 2 × 7 × (1 + 0) = 238 мм

Наибольший диаметр червячного колеса d АМ, мм определяем по формуле

d АМ ≤ d а2 + 6 × m / (Z1 + 2), (50)

d АМ ≤ 238 + 6 × 7/ (2 + 2) = 248,5 мм

Диаметр впадин зубьев червячного колеса d F2, мм определяем по формуле

d F2 = d2 - 2 × m × (1,2 - Х), (51)

d F2 = 224 - 2 × 7 × (1,2 - 0) = 207,2 мм

Ширину венца червячного колеса b2, мм, при Z1 =2, определяем по формуле

b2 = 0,355 × аW, (52)

b2 = 0,355 × 140 = 49,7 мм

Принимаем b2 = 48 мм

Радиусы закруглений зубьев червячного колеса Rа и RF, мм определяем по формулам

Rа = 0,5 × d1 - m, (53)

Rа = 0,5 × 56 - 7 = 21 мм

RF = 0,5 × d1 + 1,2 × m

RF = 0,5 × 56 + 1,2 × 7 = 36,4 мм (54)

Условный угол обхвата червяка венцом колеса определяем по формуле

sin σ = b2/ (d а1 - 0,5 × m), (55)

sin σ = 48/ (70-0,5 × 7) = 0,721805

Угол σ = 46 o 12, 2 × σ = 92 o24/< 120 о

Коэффициент полезного действия червячной передачи ŋ, определяем по формуле

ŋ = tgY/ tg (Y + φ), (56)

где φ - угол трения зависящий от скорости скольжения.

Скорость скольжения Vs, м/с определяем по формуле

Vs = Uф × ω2 × d1 / (2 × cos y × 10 3), (57)

Vs = 16 × 9,39 × 56/ (2 × cos (14 o 03 /) × 1000) = 4,34 м/с

По таб.4.9 c 74 [1] выбипаем φ = 1 o50 /.

Тогда по формуле (56)

ŋ = tg (14 o 03 /) / tg (14 o 03 /+ 1 o 50 /) = 0,9

Проверим контактные напряжения зубьев колеса

σ H = 340 ×  < [σ] H, (58)

где К - коэффициент нагрузки, зависящий от окружной скорости, К = 1

Окружную силу на колесе Ft2, кН определяем по формуле

Ft2 = 2 × T2 × 10 3/d2, (59)

Ft2 = 2 × 231,16 × 1000/224 = 2,0639 кН

Окружную скорость червячного колеса Vs, м/с определяем по формуле

Vs = ω2 × d2/ (2 × 10 3), (60)

Vs = 9,39 × 224/2 × 10 3 = 1,05 м/с < 3 м/с

Найденные значения подставляем в формулу (58)

σ H = 340 × = 137,91 Н/мм 2 < [σ] H = 151 Н/мм 2

Недогруз 100% × ([σ] H - σ H) / [σ] H

100% × (151 - 137,9) / 151 = 8,67% < 15% условие выполняется.

Проверим напряжения изгиба зубьев колеса

σ F = 0,7 × YF × Ft 2 × K/ (b2 × m) < [σ] F, (61)

где YF - коэффициент формы зуба колеса, определяемый по таб.4.10 [1] в зависимости от эквивалентного числа зубьев.

Эквивалентное число зубьев Zυ 2, определяем по формуле

Zυ 2 = Z2/ (cos y) 3, (62)

Zυ 2 = 32/ cos 3 (14 o 03 /) = 35,05

Тогда YF = 1,64.

Подставляем найденные значения в формулу (61)

σ F = 0,7 × 1,64 × 2063,9 × 1/ (48 × 7) = 7,05 Н/мм 2 < [σ] F = 112 Н/мм 2

При проверке на прочность получаем σ H < [σ] H, σ F < [σ] F, следовательно, рассчитанная червячная передача соответствует рабочим нагрузкам.

Таблица 3 - Параметры червячной передачи

Межосевое расстояние аW= 140 мм Модуль m = 7 мм
Червяк		Колесо
Параметр	Знач.	Параметр	Знач.
Делительный диаметр d1, мм	56	Делительный диаметр d2, мм	224
Начальный диаметр d W 1,, мм	56	Диаметр вершин зубьев d а2, мм	238
Диаметр вершин витков d а1, мм	70	Наибольший диаметр колеса d АМ, мм	248,5
Диаметр впадин витков d F1, мм	39,2	Диаметр впадин зубьев d F2, мм	207,2
Делительный угол подъема линии витков Y	14 o 03 /	Ширина венца при b2, мм	48
Длина нарезаемой части червяка b1, мм	84	Радиусы закруглений зубьев Rа, мм RF, мм	21 36,4
КПД червячной передачи η	0,9	Условный угол обхвата червяка венцом колеса 2× σ	92 o28 /
Контактные напряжения зубьев колеса σ H, Н/мм 2	137,91	Напряжения изгиба зубьев колеса σ F, Н/мм 2	7,05

5. Расчет открытой косозубой зубчатой передачи

Проектный расчет

Межосевое расстояние аW, мм определяем по формуле

аW ≥ Ка × (U + 1) × 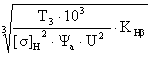, (63)

где Ка - вспомогательный коэффициент для косозубых передач, Ка = 43;

ψа - коэффициент ширины венца колеса, при консольном расположении колеса ψа = 0,2……0,25

принимаем ψа = 0,25;

U - передаточное число, U2 = 2,5;

Т - вращающий момент на валу ведущей звездочки, Т3 =543,51 Н м;

[σ] H - среднее допускаемое контактное напряжение, [σ] H = 456,8 Н/мм 2;

КHb - коэффициент неравномерности нагрузки по длине, КHb = 1,05.

аW ≥ 43 × (2,5 + 1) × 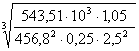 = 174,65 мм

Округляем расчетное межосевое расстояние до стандартного аW = 180 мм.

Модуль зацепления m, мм определяем по формуле

m ≥ 2 × Km × T3 × 10 3/ (d2 × b2 × [σ] F), (64)

где Km - вспомогательный коэффициент, Km = 5,8.

Делительный диаметр колеса d2, мм определяем по формуле

d2 = 2 × аW × U1 / (U1 + 1), (65)

d2 = 2 ×180 × 2,5/ (2,5 + 1) = 257,14 мм

Ширину венца b2, мм определяем по формуле

b2 = ψа × аW, (66)

b2 = 0,25 × 180 = 50,4 мм

Подставляем найденные значения в формулу (64)

m ≥ 2 × 5,8 × 543,51 × 10 3/ (257,14 × 50,4 × 170,75) = 2,85 мм

Принимаем m =3 мм.

Угол наклона зубьев βмин, о определяем по формуле

βмин = arcsin (3,5 × m / b2), (67)

βмин = arcsin (3,5 × 3/50,4) = arcsin (0, 20833) = 12 о02 /

Числа зубьев шестерни Z1 и колеса Z2: определяем по формулам

Z1 = Z / (1 + U1), (68), Z1 = 117/ (1 + 2,5) = 33,43

Принимаем Z1 = 33

Z2 = Z - Z1,Z2 = 117 - 33 = 84

Суммарное число зубьев Z определяем по формуле

ZS = 2 × аW × cos βмин / m, (69)

ZS = 2 × 180 × 0,9781/3 = 117,37

Принимаем ZS = 117

Уточненный угол β, о определяем по формуле

β = arcos (ZS × m /2 × aW), (70)

β = arcos (117 × 3/2 × 180) = 12 о 51 /

Фактическое передаточное число Uф и его отклонения от заданного ΔU определяем по формулам

Uф = Z2/ Z1, (71), Uф = 84/33 =2,55

ΔU = (Uф -U) × 100% / U £ 4%, (72)

ΔU = (2,55 - 2,5) × 100% / 2,5 = 1,82% £ 4%

Фактическое межосевое расстояние аW, мм определяем по формуле

аW = (Z1 + Z2) × m/ (2 × cos β), (73)

аW = (33 + 84) × 3/ (2 × 0,9781) = 180 мм

Делительный диаметр шестерни d1, мм определяем по формуле

d1 = m × Z1/cos β, (74)

d1 = 3 × 33/0,9781 = 101,5 мм

Диаметр вершин зубьев шестерни dа1, мм определяем по формуле

dа1 = d1 + 2 × m,

dа1 = 101,5 + 2 × 3 = 107,5 мм (75)

Диаметр впадин зубьев шестерни df1, мм определяем по формуле

df1 = d1 - 2,4 × m, (76)

df1 = 101,5 - 2,4 × 3 =94,3 мм

Ширина венца шестерни b1, мм определяем по формуле

b1 = b2 + 4, (77)

b1 = 50 + 4 = 54 мм

Принимаем b1 = 54 мм.

Делительный диаметр колеса d2, мм определяем по формуле

d2 = m × Z2/cos β, (78)

d2 = 3 × 84/0,9781 = 258,5 мм.

Диаметр вершин зубьев колеса dа2, мм определяем по формуле

dа2 = d2 + 2 × m, (79)

dа2 = 258,5 +2 × 3 = 264,5 мм

Диаметр впадин зубьев колеса df2, мм определяем по формуле

df2 = d2 - 2,4 × m, (80)

df2 = 258,5 - 2,4 × 3 = 251,3 мм

Ширина венца колеса b2, мм определяем по формуле

b2 = ψа × аW, (81)

b2 = 0,25 × 180 = 50,4 мм

Принимаем b2 = 50 мм.

Проверочный расчет

Проверим контактные напряжения зубьев колеса

σ H = 376 × 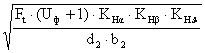 £ [σ] H, (82)

где КHa - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями по графику рис.4.2 с.63 [1], КHa = 1,1;

КHu - коэффициент динамической нагрузки, зависящий от окружной скорости и степени точности по таб.4.3 с.62 [1], КHu = 1,1;

КHb - степень точности зубчатой передачи, в зависимости от окружной скорости.

Окружную скорость Vs, м/с определяем по формуле

Vs = ω2 × d2/ (2 × 10 3), (83)

Vs = 3,75 × 258,5/ 2 × 10 3 = 0,48 м/с

Тогда по т.4.2 [1] - 9 КHb = 1,05.

Окружную силу на колесе Ft2, кН определяем по формуле

Ft2 = 2 × T2 × 10 3/d2, (84)

Ft2 = 2 × 543,51 × 10 3/258,5 = 4, 205 кН

Подставляем найденные значения в формулу (82)

σ H = 376 × = 434,06 Н/мм 2

σ H = 434,06 Н/мм 2 < [σ] H = 456,8 Н/мм 2

Недогруз 100% × ([σ] H - σ H) / [σ] H

100% × (456,8 - 434,06) / 456,8 = 4,98% < 10%, что допустимо.

Проверим напряжения изгиба зубьев колеса

σ F2 = YF2 × Yb × Ft 2 × KFa × КFb × КFu/ (b2 × m) < [σ] F2, (85)

σ F1 = σ F2 × YF1/YF2 < [σ] F1, (86)

где KFa - коэффициент, учитывающий распределение нагрузки между зубьями для степени

точности 9 с.63 [1], KFa = 1,1;

КFb - коэффициент неравномерности нагрузки по длине зуба, КFb = 1,05;

КFu - коэффициент динамической нагрузки, зависящий от окружной скорости и степени

точности по таб.4.3 с.62 [1], КFu = 1,01;

YF1 и YF2 - коэффициенты формы зуба колеса определяемый по таб.4.4 с.64 [1] в

зависимости от эквивалентного числа зубьев

Zυ 1 = Z1/ (cos β) 2, (87)

Zυ 1 = 33/0,9781 2 = 34,71

Zυ 2 = Z2/ (cos β) 3, (88)

Zυ 2 = 84/0,9781 3 = 90,6

Тогда по таб.4.4 с.64 [1] YF1 =3,75 и YF2 =3,60.

Коэффициент учитывающий наклон зуба Yb, определяем по формуле

Yb = 1 - β о/140, (89)

Yb = 1 - 12 о51 // 140 = 0,91

Тогда по формуле (85) и (86)

σ F2 = 3,6 × 0,91 × 4205,73 × 1,1 × 1,05 × 1,01/ (50 × 3) = 103,59 Н/мм 2< [σ] F = 170,75 Н/мм 2

σ F1 = 103,59 × 3,75/ 3,6 = 107,91 Н/мм 2 < [σ] F1 =192 Н/мм 2

При проверке на прочность определили что, рассчитанная передача соответствует рабочим нагрузкам.

Межосевое расстояние аW, мм определяем по формуле

аW = (d1 + d2) / 2, (90)

аW = (101,5 + 258,5) /2 = 180 мм

Пригодность заготовок шестерни и колеса определяем по формулам

Условие пригодности Dпред > Dзаг, Sпред > Sзаг

Dзаг1 = dа1 + 6, (91)

Dзаг1 =107,5 + 6 =113,5 мм < 125 мм - пригодно

Dзаг2 = dа2 = 264,5 мм - без ограничений

Sпред = 80 мм > Sзаг = b2 + 4 = 54 мм

Составим таблицу

Таблица 4 - Параметры косозубой открытой передачи

Открытая косозубая передача
Параметр	Значение
	Шестерня	Колесо
Межосевое расстояние, аW (мм)	180
Модуль зацепления, m (мм)	3
Угол наклона зубьев, βо	12 о51 /
Числа зубьев Zi	33	84
Делительный диаметр, di (мм)	101,5	258,5
Диаметр вершин dаi (мм)	107,5	264,5
Диаметр впадин dFi (мм)	94,3	251,3
Ширина венца b, (мм)	54	50
Контактные напряжения зубьев, Н/мм 2	434,06
Напряжения изгиба зубьев, Н/мм 2	103,59	107,91

Страницы: 1, 2, 3