Курсовая работа: Привод к скребковому конвееру

Курсовая работа: Привод к скребковому конвееру

Содержание

Введение

1. Кинематический расчет и выбор электродвигателя

2. Расчет механических передач

3. Проектировочный расчет валов

4. Эскизная компоновка

5. Подбор и проверочный расчет шпонок

6. Расчет элементов корпуса

7. Подбор и расчет муфты

8. Расчетные схемы валов

9. Подбор подшипников качения

10. Проверочный расчет валов на выносливость

11. Выбор типа смазывания

12. Выбор посадок

13. Технико-экономическое обоснование конструкций

14. Сборка редуктора

Список литературы

Введение

Цель проекта – проектирование привода к скребковому конвейеру. Приводная установка включает: двигатель, клиноременную передачу, упругую муфту с торообразной оболочкой, ЦР с шевронными зубьями. Вращательное движение от электродвигателя по средствам ременной передачи сообщается ведущему валу редуктора, а затем через цилиндрическую передачу с шевронным зубом – на выходной вал редуктора. Далее через муфту передается на вал скребкового конвейера.

Редуктор – механизм представляющий совокупность зубчатых или червячных передач помещенных в корпус, который являются для них масляной ванной. Назначение редуктора – понижение угловых скоростей ведомых звеньев с одновременным повышением вращающих моментов.

Муфта – устройство предназначенное для соединения валов между собой или валов с посаженными на них деталями и передачи вращающего момента без изменения величины и направления.

Конвейер – транспортирующие устройство для перемещения грузов.

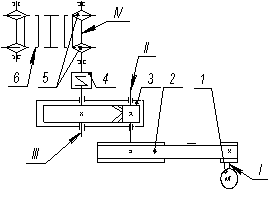
Привод к скребковому конвейеру

1 – двигатель; 2 – клиноременная передача; 3 – цилиндрический редуктор; 4 – упругая муфта с торообразной формой; 5 – ведущие звездочки конвейера; 6 – тяговая цепь. I, II, III, IV – валы, соответственно, - двигателя, быстроходный и тихоходный редуктора, рабочей машины

Таблица 1 – Исходные данные

Исходные данные	Вариант № 6
Тяговая сила цепи F,кН Скорость тяговой цепи ט, м/с Шаг тяговой цепи Р, мм Число зубьев звездочки z Допускаемое отклонение скорости тяговой цепи δ, % Срок службы привода L, лет	3,5 0,60 80 7 5 4

1. Кинематический расчет и выбор электродвигателя

Мощность на выходном валу привода

Р4 = Ftυ       (1.1)

Р4 = 3,5· 0,6 = 2,1 кВт

Общий КПД привода

η=η1·η2·η3·η43       (1.2)

где, η1 = 0,97 – КПД ременной передачи;

η2 = 0,98 – КПД зубчатой передачи;

η3 = 0,98 – КПД муфты;

η4 = 0,99 – КПД одной пары подшипников качения.

[1; с. 42]

Следовательно

η = 0,97·0,98·0,98·0,993 = 0,904

Требуемая мощность электродвигателя

Рдвтр = Р4/η           (1.3)

Рдвтр = 2,1 /0,904=2,32 кВт

По таблице 24.9 [2; с. 417] принимаем асинхронный электродвигатель АИР 112МА6, имеющий мощность Рном = 3 кВт, и частоту вращения n дв = 950 мин-1

Частота вращения выходного вала привода

n4=60·103·υ/Р·z             (1.4)

n4=60·103·0,6/80·7=64,28 мин -1

Общее передаточное число привода

u= n1 / n4                       (1.5)

где n1 = n дв = 950 мин-1

u =950/64,28=14,78

Передаточные числа двух степеней привода

Так как u= u1 · u2 ,то приняв стандартное значение передаточного числа редуктора u2=4, получим передаточное число ременной передачи

u1 = u/ u2                       (1.6)

u1= 14,78 /4 = 3,69

Частота вращения валов привода

n1= 950 мин-1 ;     (1.7)

n2= n1/ u1 =950/3,69=257,1 мин-1 ;

n3= n2/ u2 = 257,1 / 4 =64,28 мин-1 ;

n4= n3 =64,28 мин-1

Угловая скорость вращения валов привода

ω1=π n1/30 = π·950/30=99,4 рад/с ;                   (1.8)

ω2= ω1/ u1 =99,4/3,69=26,9 рад/с ;

ω3= ω2/ u2 =26,9 /4=6,73 рад/с ;

ω4= ω3=6,73 рад/с

Проверка: ω4= π n4/30=π·64,28/30=6,73 рад/с

Мощность на валах привода

Р1= Рдвтр =2,32 кВт;

Р2= Р1 · η1 · η4 =2,32·0,97·0,99=2,23 кВт;

Р3= Р2 · η2· η4 =2,16·0,98·0,99=2,16 кВт;

Р4= Р3 · η3 · η4 =2,16·0,98·0,99=2,1 кВт

Вращающие моменты на валах привода

Т = 9550Р/n                  (1.9)

Т1=9550 Р1 / n1=9550·2,32/950=23,35 Нм;

Т2=9550 Р2/ n2=9550·2,23 /257,1=82,9 Нм;

Т3=9550 Р3/ n3=9550·2,16 /64,28= 321,7 Нм;

Т4=9550 Р4/ n4=9550·2,1/64,28=312,0 Нм

Проверка: Т4= Т1·u· η =23,35·14,78·0,904=312,0 Нм

Результаты расчетов сводим в таблицу 1

Таблица 1 – Кинематические и силовые параметры привода

№ вала	n , мин-1	ω , рад/с	Р , кВт	Т , Нм	u = 14,78
I	950	99,4	2,32	23,35	u1=3,69
II	257,1	26,9	2,23	82,9
III	64,28	6,73	2,16	321,7	u2=4
IV	64,28	6,73	2,1	312,0	_

2. Расчет механических передач

Расчет цилиндрической передачи с шевронным зубом

Выбор материала

Для изготовления шестерни и колеса принимаем наиболее распространенную сталь 45 с термообработкой-улучшение. По таблице 9.2 [3,с.170]выбираем: для шестерни твердость 269…302 НВ, σТ=650 МПа, при предполагаемом диаметре заготовки шестерни D≤650 мм; для колеса твердость 235..262 НВ2, σТ=540 МПа, при предполагаемой ширине заготовки колеса S≤80 мм. Из табличных данных выбираем примерно среднее значение твердости как наиболее вероятное. Принимаем: твердость шестерни 280 НВ1; колеса – 260 НВ2. При этом НВ1 –НВ2=280-250=40 – условие соблюдается.

Допускаемые контактные напряжения

σНР =σНО·zН·0,9/SН                              (2.1)

где σно – предел контактной выносливости;

σНО=2НВ+70       (2.2)

σНО1=2НВ1+70=2·280+70=630 МПа;

σНО2=2НВ2+70=2·250+70=570 МПа;

zН=1- коэффициент долговечности (для длительных рабочих передач)

SН=1,1 – коэффициент запаса прочности для улучшенных колёс,[3; с. 187]

σНР1=630·1·0,9/1,1=516 МПа

σНР2=570·1·0,9/1,1=466 МПа

σНР=0,45(σнр1+ σнр2)≥ σнрmin                 (2.3)

σНР=0,45(516+466) = 442 МПа – условие не выполняется

Принимаем σНР=466 МПа

Допускаемые напряжения изгиба

σFР=σFО ·ΥN/ SF                       (2.4)

где σFО - предел изгибной выносливости соответствующий базовому числу циклов напряжений

σFО= 1,8НВ          (2.5)

σFО1= 1,8НВ1=1,8·280=504 МПа;

σFО2= 1,8НВ2=1,8·250=450 МПа;

ΥN =1 – коэффициент долговечности [3; с.194];

SF =1,75 – коэффициент запаса прочности [3; с.194];

σFР1=504·1/1,75=288 МПа;

σFР2 =450·1/1,75=257 Мпа

Расчетные коэффициенты

Ψba=0,4 [3; с.191];

КНβ=1, по таблице 9.45 [3; с.192]

Межосевое расстояние передачи

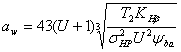            (2.6)

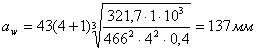
Принимаем стандартное значение αW=140 мм [3; с.171]

Ширина зубчатого венца

b2= Ψba· αW                  (2.7)

b2=0,4·140=56 мм

Нормальный модуль зубьев

mn= (0,01…0,02) αW                        (2.8)

mn= (0,01…0,02) 140 = 1,2…2,8 мм

Принимаем стандартное значение mn= 2 мм [3; с.157]

Принимаем минимальный угол наклона зубьев βmin=25º и определяем суммарное число зубьев

z∑ = (2 αW · cosβmin)/ mn                 (2.9)

z∑ = (2·140· cos25º)2=126,2

Принимаем z∑ = 126

Фактический угол наклона зубьев

cosβ= mn z∑/2 αW                 (2.10)

cosβ=2·126/2·140=0,9;β=25º49´

Число зубьев шестерни и колеса

z1= z∑/(u+1)                   (2.11)

z1=126/(4+1)=25

z2= z∑ - z1

z2=126-25=101

Фактическое передаточное число

uф= z2/ z1                       (2.12)

uф=101/25=4,04;∆u=(u - uф )/u·100%≤4%

∆u=(4-4,04)/4·100%=1%≤4%

Основные геометрические размеры передачи

d= mn z/ cosβ                 (2.13)

d1=2·25/cos25º49´=56мм;

d2=2·68/ cos25º49´=224мм

Уточняем межосевое расстояние

αW =( d1 + d2 )/2 =140 мм        (2.14)

Диаметры окружностей вершин зубьев шестерни и колеса:

dа=d + 2 mn                                               (2.15)

dа1=56+2·2=60мм;

dа2=224+2·2=228мм

Ширина зубчатых колес с учетом дорожки α для выхода червячной фрезы, при mn=2мм

α=14 mn                         (2.16)

α=14·2=28 мм

b´=b+α=56+28=89 мм

Окружная скорость колес и степень точности передачи

υ=π· d1· n1/60                (2.17)

υ=π·56·10-3/60=0,76 м/с

по таблице 9.1 [3;с.163] принимаем 8-ю степень точности

Силы в зацеплении

Ft=2T2/d2 – окружная            (2.18)

Ft=2·321,7·103/224= 2872 Н

Fr= Fttq20º/cosβ – радиальная                 (2.19)

Fr=2872·tq20º/ cos25º49´=1158 Н

Уточняем значение коэффициентов

Ψd=b2/d1                        (2.20)

Ψd=56/56=1

При этом КНВ=1, по таблице 9.5 [3;с.192]

Принимаем коэффициенты

Кнυ=1,1, по таблице 9.6 [3;с.193] ;

Кна =1,12, по таблице 9.6 [3;с.193]

Расчетное контактное напряжение

σн=266/ αW uф√Т2 Кна Кнβ Кна (uф +1)3                              (2.21)

σн=266/140·4,04√321,7·103·1·1,1·1,12(4+1)3=447 МПа

Н=466-447/466·100%=4%,что допустимо

Проверочный расчет зубьев на изгиб. Этот расчет выполняется по зубьям шестерни. Это объясняется тем, что материал шестерни и колеса одинаков, но толщина зубьев шестерни у основания ножки меньше, чем у зубьев колеса, поэтому и прочность их ниже по сравнению с прочностью зубьев колеса.

Эквивалентное число зубьев шестерни

zV1= z1/ cos 3β                (2.22)

zV1=25/ cos 325º49´=34,5

zV= 101/ cos 325º49´=138,5

Коэффициент формы зуба

ΥF1=3,9; ΥF1=3,6 [3;с.185]

Принимаем коэффициенты

КFB=1,3

KFυ=1,2 KFα=0,91

ΥВ =1- βº/140º=1-25º49´/140=0,818 [3;с.192]

Расчетное напряжение изгиба

σF2= ΥF1 ΥВ Ft / b2 mnKFαKFυКFB                           (2.24)

σF2=3,9·0,818·2872/56·2·0,91·1,3·1,2=116 МПа

σF1= σF2 ΥF1 / ΥF2 =116·3,9/3,6=126 МПа          (2.25)

σF1=116·3,9/3,6=126 МПа

Результаты расчетов сводим в таблицу 2

Таблица 2 – Параметры зубчатой цилиндрической передачи,мм

Проектный расчет
Параметр	Значение	Параметр	Значение
Межосевое расстояние αW	140	Угол наклона зубьев β	25º49´
Модуль зацепления mn	2	Диаметр делительной окружности шестерни d1 колеса d2	56 224
Ширина зубчатого венца: шестерни b1 колеса b2	60 56
Число зубьев шестерни z1 колеса z2	25 101	Диаметр окружностей вершин шестерни dа1 колеса dа2	60 228
Вид зубьев	шевронный зуб	Диаметр окружности вершин шестерни df1 колеса df2	51 223
Проверочный расчет
Параметр	Допускаемое значение	Расчетное значение	Примечание
Контактное напряжение σ	466 МПа	447 МПа	Контактная выносливость обеспечена
Напряжения изгиба σFО1 σFО2	504 МПа	126 МПа	Изгибная выносливость зубьев обеспечена
	450 МПа	116 МПа

Страницы: 1, 2, 3