Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления

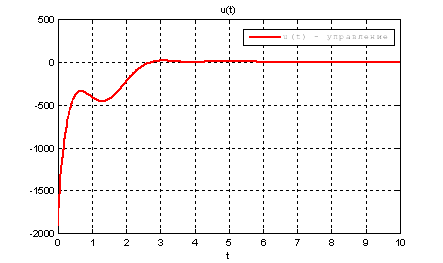
Рис.25. График управления.

Выводы: т.к. решения уравнения Риккати методом диагонализации и интегрирования в обратном времени дают практически одинаковый результат, то можно считать, что задача АКОР – стабилизации на полубесконечном интервале решена с заданной точностью.

5.2 Стабилизации объекта управления на конечном интервале времени

Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме

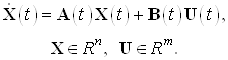
Начальные условия для заданной системы

Время стабилизации .

Необходимо получить закон управления

минимизирующий функционал вида

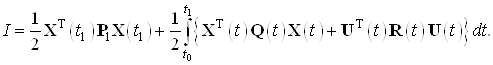
Закон оптимального управления в данной задаче имеет вид

Матричное дифференциальное уравнение Риккати будет иметь следующий вид:

Если обозначить  то можно записать

Уравнение замкнутой скорректированной системы примет вид

Матрицы заданы в пункте 5.1.1.

Весовые матрицы и имеют следующий вид:

, .

Используя скрипт AKOR_stabilizaciya_na_konech_interval.m получили следующие результаты:

Рис.26. Графики решения уравнения Риккати.

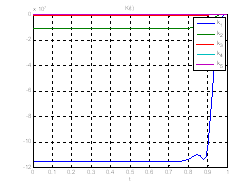
Рис.27. Графики коэффициентов регулятора обратной связи.

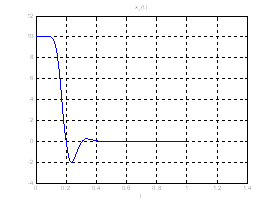
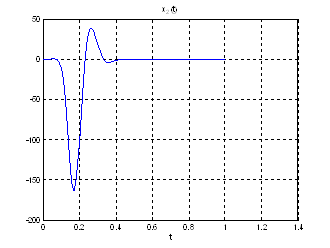
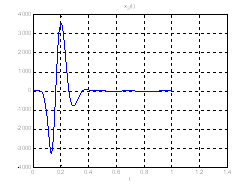
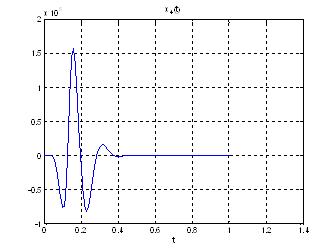
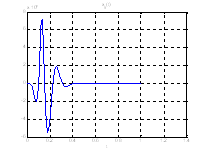
Рис.28. Графики фазовых координат.

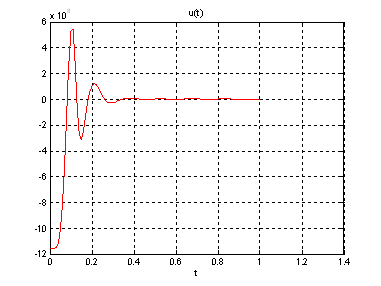
Рис.29. График управления.

Сравним, как стабилизируется система управления с постоянными и переменными коэффициентами регулятора обратной связи на начальном этапе:

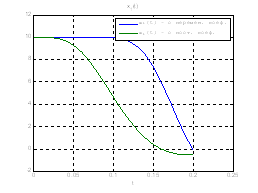
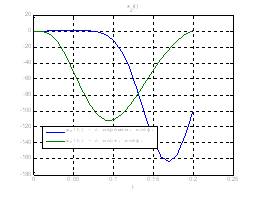
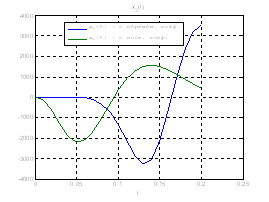
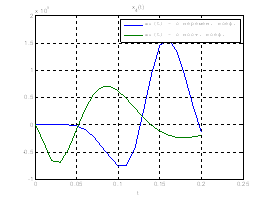
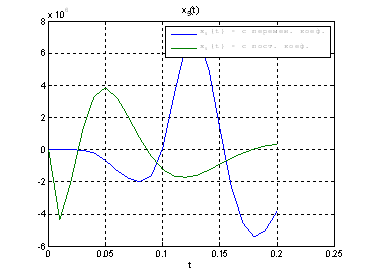
Рис.30. Графики фазовых координат.

Выводы: из графиков видно, что система, у которой коэффициенты регулятора меняются со временем, стабилизируется не хуже, чем, система, у которой коэффициенты регулятора не изменяются.

5.3 Задача АКОР – стабилизации для компенсации
известного возмущающего воздействия

Рассмотрим систему вида

,

где  – возмущающее воздействие.

Матрицы заданы в пункте 5.1.1.

Весовые матрицы и имеют следующий вид:

, .

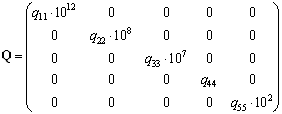Начальные условия для заданной системы .

Время стабилизации .

Задаем возмущающее воздействие только на первую координату, так как только она имеет значение

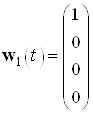 и .

Решение задачи стабилизации сводится к решению уравнения Риккати

с начальными условиями:

Введём вспомогательную вектор-функцию , ДУ которой имеет вид:

с начальными условиями: .

Управление определяется по формуле:

.

Используя скрипт AKOR_stabilizaciya_pri_vozmusheniyah.m, получили следующие результаты:

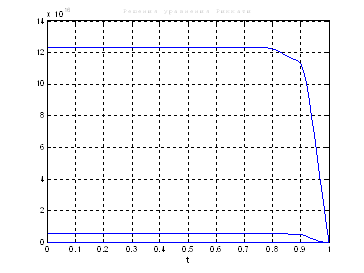
Рис.31. Графики решения уравнения Риккати.

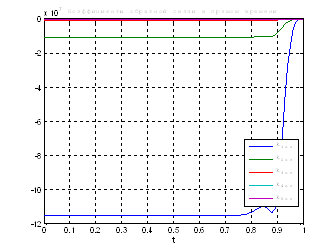
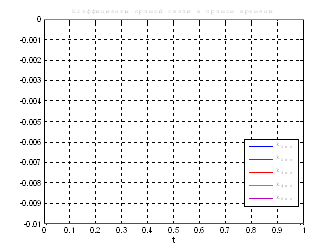
Рис.32. Графики коэффициентов регулятора обратной и прямой связи.

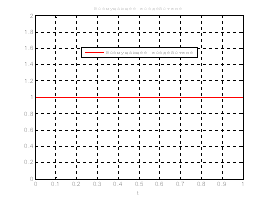
Рис.33. График возмущающего воздействия.

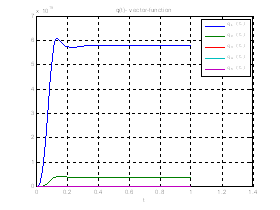
Рис.34. График вспомогательной вектор – функции.

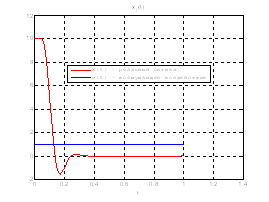
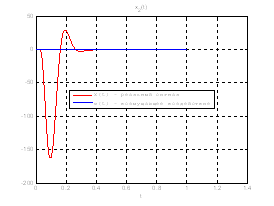
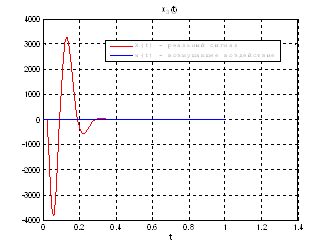
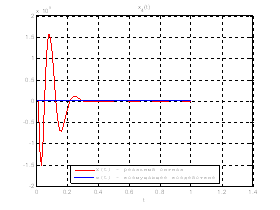
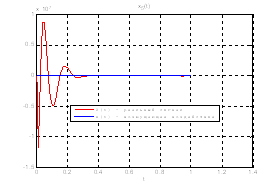
Рис.35. Графики фазовых координат.

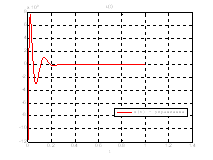
Рис.36. График управления.

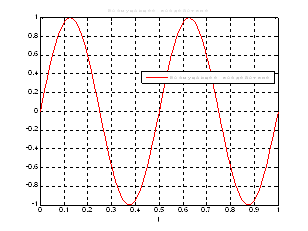
Рис.37. График возмущающего воздействия.

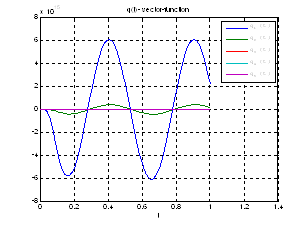
Рис.38. График вспомогательной вектор – функции.

 

 

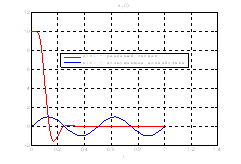
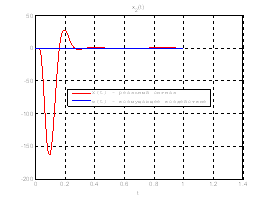
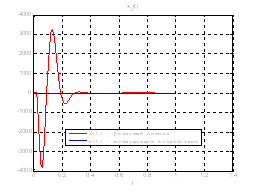
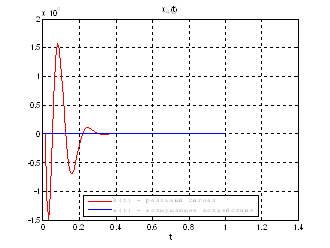
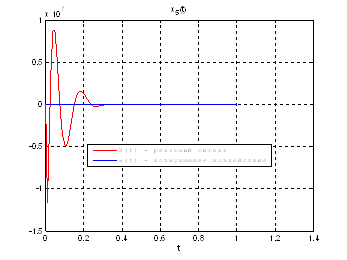
Рис.39. Графики фазовых координат.

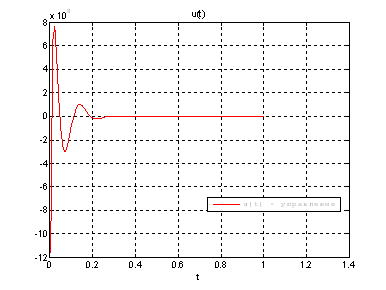
Рис.40. График управления.

Выводы: По графикам фазовых координат при различных воздействиях видно, что влияние возмущающего воздействия не существенно и фазовые координаты устанавливаются в ноль. При этом видно, что графики первой фазовой координаты при различных воздействиях мало отличаются друг от друга, т.е. система отрабатывает любое возмущение.

5.4 Задача АКОР для отслеживания известного задающего воздействия. I подход

Система задана в виде:

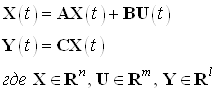
Матрицы заданы в пункте 5.1.1.

Весовые матрицы и имеют следующий вид:

, .

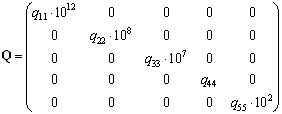Начальные условия для заданной системы .

Время слежения .

Задающее воздействие в виде системы ДУ

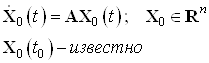
Начальные условия для воздействия:

.

Введем расширенный вектор состояния и расширенные матрицы

,

,

.

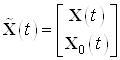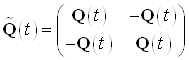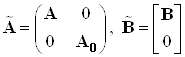Тогда новое описание системы имеет вид:

с начальными условиями: .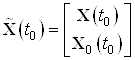

Решением уравнения Риккати будет матрица:

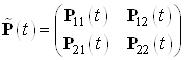
с н.у.

Тогда оптимальное управление, находится по формуле:

Используя скрипт AKOR_slegenie_na_konech_interval_I_podxod, получили следующие результаты:

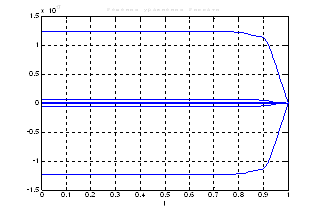
Рис.41. Графики решения уравнения Риккати.

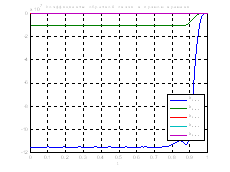
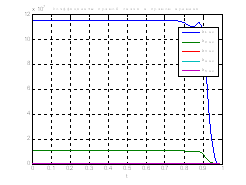
Рис.42. Графики коэффициентов регулятора обратной и прямой связи.

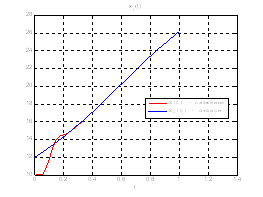
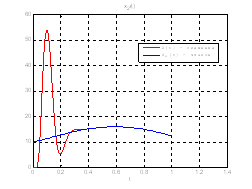
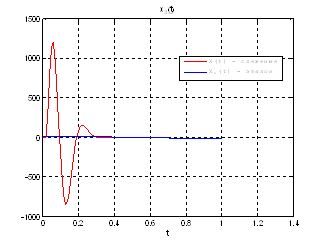
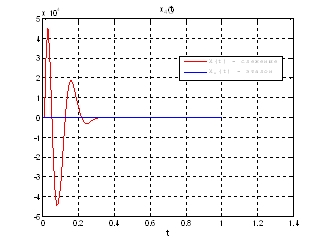
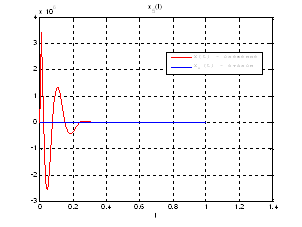
Рис.43. Графики фазовых координат.

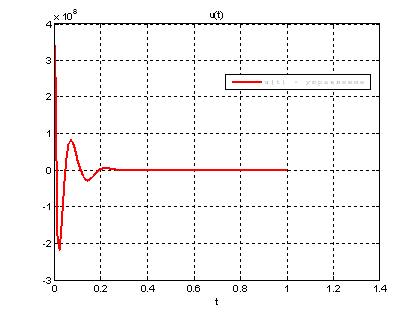
Рис.44. График управления.

Выводы: На данном этапе была решена задача АКОР-слежения. В качестве отслеживаемого воздействия была взята исходная система, но с другими начальными условиями, поэтому графики фазовых координат отличаются от заданных, но только на начальном участке движения.

5.5 Задача АКОР для отслеживания известного задающего воздействия. II подход (линейный сервомеханизм)

Система задана в виде:

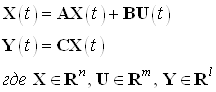
Матрицы заданы в пункте 5.1.1.

Весовые матрицы и имеют следующий вид:

, .

Начальные условия для заданной системы .

Задающее воздействие имеет вид:

, .

Время слежения

Введём вспомогательную вектор-функцию , ДУ которой определяется

,

,

НУ определяются из соотношения

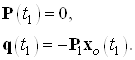
Зная закон изменения  и , можно определить управление:

.

Используя скрипт AKOR_slegenie_na_konech_interval_II_podxod, получили следующие результаты:

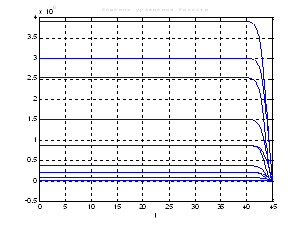
Рис.45. Графики решения уравнения Риккати.

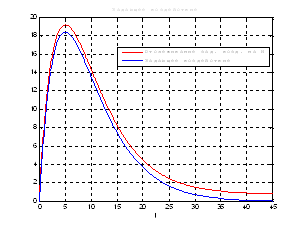
Рис.46. График задающего воздействия.

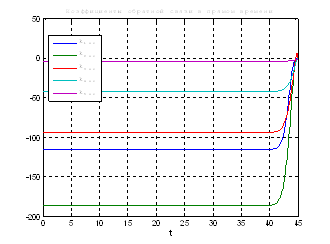
Рис.47. Графики коэффициентов регулятора обратной и прямой связи.

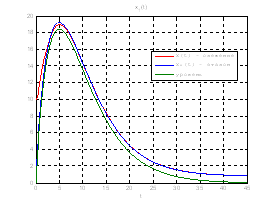
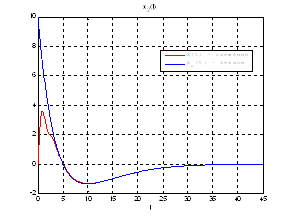
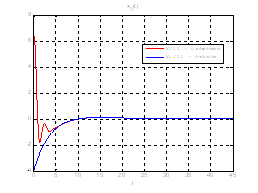
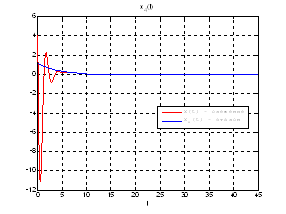
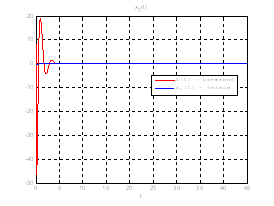
Рис.48. Графики фазовых координат.

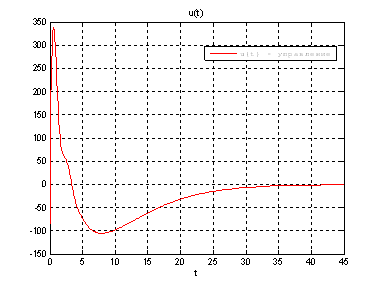
Рис.49. График управления.

Выводы: На данном этапе была решена задача построения линейного сервомеханизма. В качестве отслеживаемого воздействия была задана экспоненциальная функция. Анализируя выше приведенные графики, можно сказать, что все состояния заданной системы, особенно первая фазовая координата, отслеживается с заданной точностью.

5.6 Задача АКОР – слежения со скользящими интервалами

Пусть интервал времени  является объединением нескольких отрезков. Известно некоторое задающее воздействие  заданное аналитическим выражением, причем информация о задающем сигнале на следующем отрезке времени поступает только в конце предыдущего. Таким образом, зная задающий сигнал только на одном отрезке времени, мы будем синтезировать управление на этом отрезке.

Разобьем весь интервал на 3 равных отрезка.

Данная задача похожа на задачу отслеживания известного задающего воздействия, заданного аналитическим выражением, но с некоторыми изменениями:

1.      Поскольку в уравнение Риккати относительно матрицы  входят только параметры системы и функционала качества, то решать его будем один раз на первом отрезке, так как на остальных отрезках решение будет иметь тот же вид, но будет смещено по времени:

2.      Начальными условиями для системы на каждом отрезке будет точка, в которую пришла система на предыдущем отрезке:

3.      Вектор  необходимо пересчитывать на каждом отрезке.

4.      В остальном данная задача аналогична задаче построения линейного сервомеханизма (пункт 5.5).

Используя скрипт AKOR_slegenie_so_skolz_intervalami_Modern, получили следующие результаты:

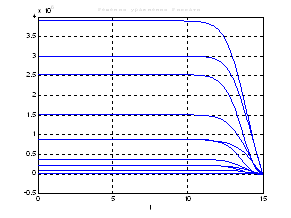
Рис.50. Графики решения уравнения Риккати.

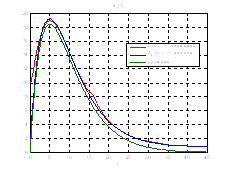
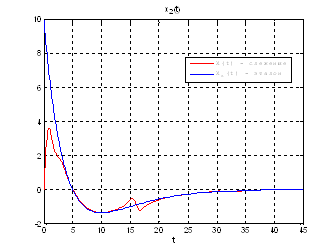
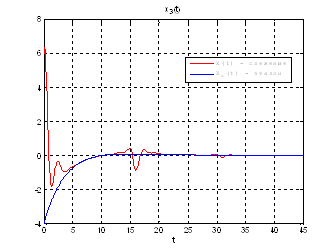
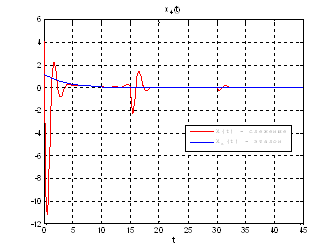
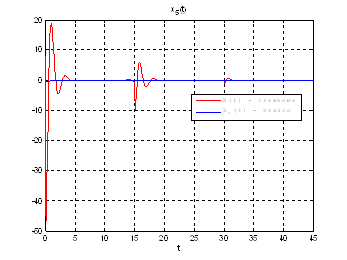
Рис.51. Графики фазовых координат.

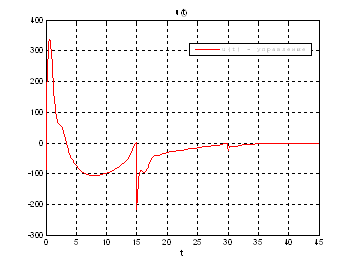
Рис.52. График управления.

Выводы: при сравнении полученных результатов, можно сказать, что различия в фазовых координатах при наличии трех участков и при наличии одного участка несущественные. Если сравнивать скорость вычислений и используемые ресурсы, то скорость увеличивается почти в 3 раза, а памяти требуется в 3 раза меньше для решения поставленной задачи. В точках соединения участков наблюдаются скачки, связанные с тем, что требуется значительные затраты на управление, но для первой координаты этот скачок незначительный.

6. Синтез наблюдателя полного порядка

Наблюдателями называются динамические устройства, которые позволяют по известному входному и выходному сигналу системы управления получить оценку вектора состояния. Причем ошибка восстановления .

Система задана в виде:

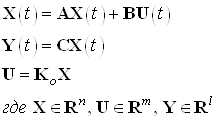
Начальные условия для заданной системы .

Матрицы заданы в пункте 5.1.1.

Весовые матрицы и имеют следующий вид:

, .

Построим наблюдатель полного порядка и получим значения наблюдаемых координат  таких, что:

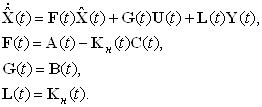
В качестве начальных условий для наблюдателя выберем нулевые н.у.:

Ранг матрицы наблюдаемости:

 - матрица

наблюдаемости.

.

.

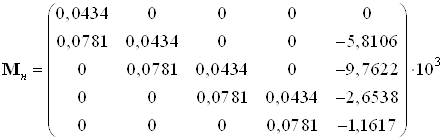Т. е. система является наблюдаемой.

Коэффициенты регулятора:

,

тогда

Собственные значения матрицы :

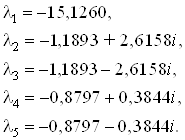
Коэффициенты наблюдателя выберем из условия того, чтобы наблюдатель был устойчивым, и ближайший к началу координат корень матрицы  лежал в 3 – 5 раз левее, чем наиболее быстрый корень матрицы . Выберем корни матрицы

 

Коэффициенты матрицы наблюдателя:

.

Используя скрипт Sintez_nablyud_polnogo_poryadka, получили следующие результаты:

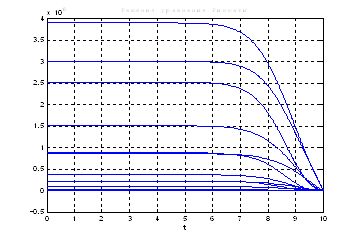
Рис.53. Графики решения уравнения Риккати.

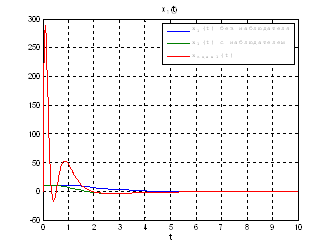
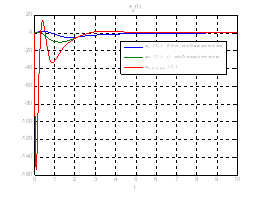
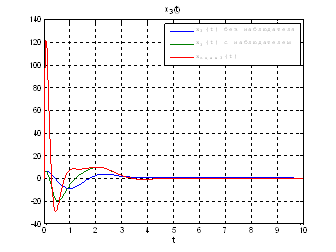
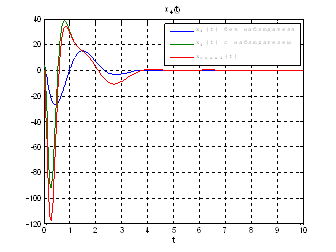
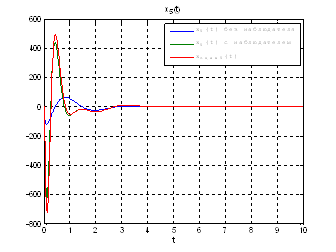
Рис.54. Графики фазовых координат.

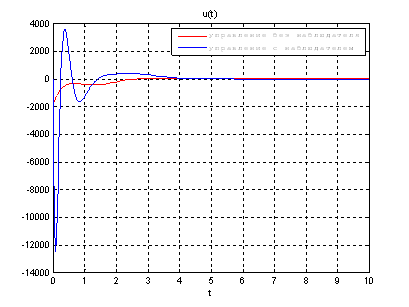
Рис.55. Графики управлений.

Выводы: Так как система является полностью наблюдаема и полностью управляема, то спектр матрицы  может располагаться произвольно. Перемещая собственные значения матрицы  левее, относительно собственных значений матрицы  мы улучшаем динамику системы, однако, наблюдатель становится более чувствителен к шумам.

Литература

Страницы: 1, 2, 3, 4, 5, 6, 7