Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления

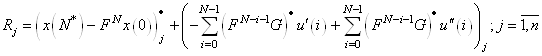
и подставим в целевую функцию. Получим  – строку

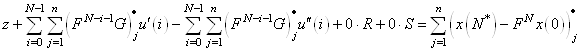  (15)

Решаем задачу (12) – (14) симплекс-методом.

В случае,

если ,  – малое число

иначе

1) если  увеличить  и целое,рвернуться к первому шагу формирования задачи линейного программирования;

2) если  (не все управления будут равны предельным, могут быть, в том числе нулевые)), , уменьшить , вернуться к первому шагу формирования задачи линейного программирования.

Решения данной задачи получено с помощью пакета Matlab 7.4 (скрипт SimplexMetod2.m):

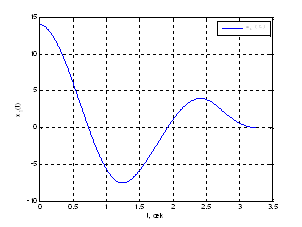
Рис. 14. График фазовой координаты .

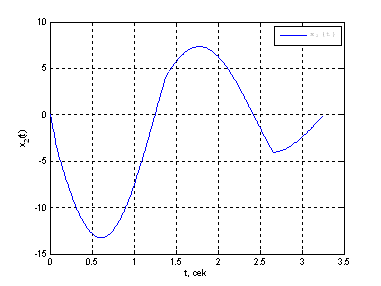
Рис. 15. График фазовой координаты .

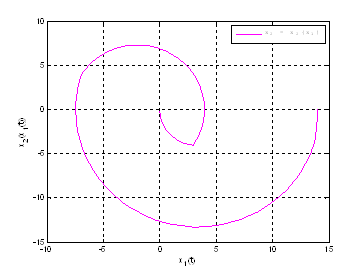
Рис. 16. График .

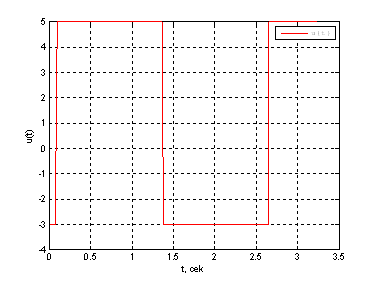
Рис. 17. График оптимального управления .

Выводы: Сравнивая полученные результаты с результатами полученными в ДЗ№2 по СУЛА, можно сделать вывод, что решения совпадают, с точностью до .

3. Оптимальная L – проблема моментов

 

3.1 Оптимальная L – проблема моментов в пространстве «вход-выход»

Укороченная система данного объекта имеет вид:

,

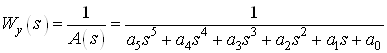где:

;

;

;

;

;

.

Полюса укороченной передаточной функции:

;

;

;

;

.

Заданы начальные и конечные условия:

, , .

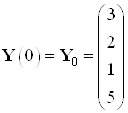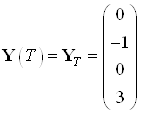Для определения начальных и конечных условий для  воспользуемся следующей формулой:

,

Где матрица  имеет следующий вид

,

где , .

ИПФ укороченной системы:

Составим фундаментальную систему решений:

ФСР: .

Составим матрицу .

, где  – матрица Вронского

,

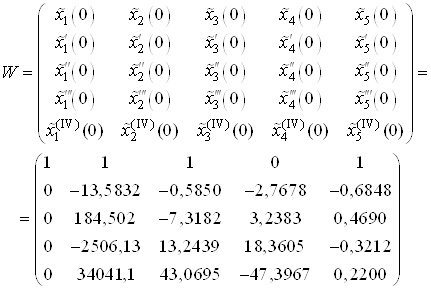
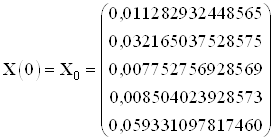Тогда

.

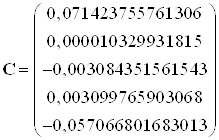Составим моментные уравнения (связь между входом и выходом):

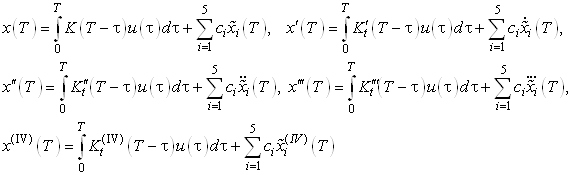
Моментные функции определяются по следующей формуле

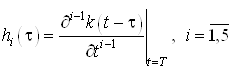
Составим моментные функции:

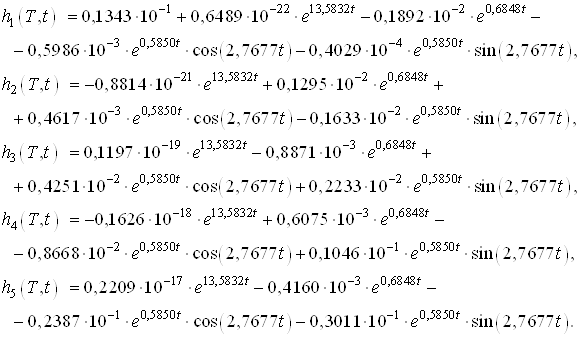
Найдем моменты по следующей формуле:

.

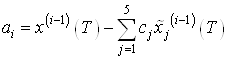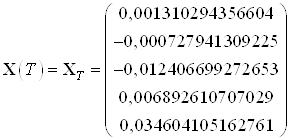
Числовое значение найденных моментов:

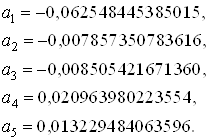
Составим функционал качества, который имеет следующий вид:

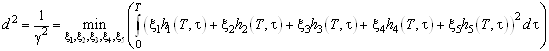
при условии, что :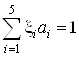, т.е.

Выразим из данного условия , тогда получим следующее равенство:

.

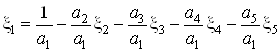Подставляя полученное равенство в функционал и заменяя  их правыми частями получаем

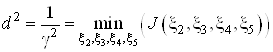
Найдем частные производные 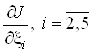 и приравняем их к нулю. Решая полученную систему уравнений, определяем оптимальные значения коэффициентов , а  вычислим по формуле

.

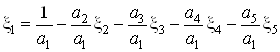Т.о. имеем:

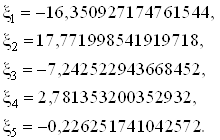
Минимальная энергия:

Найдем управление по следующей формуле:

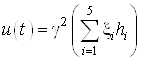
Тогда оптимальное управление

.

3.2 Оптимальная L – проблема моментов в пространстве состояний

Система задана в виде:

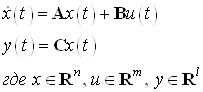
Решение ДУ имеет вид:

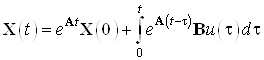, при  имеем:

.

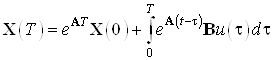Составим моментные уравнения:

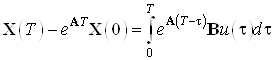
Подставляя необходимые данные в выше приведенные формулы, получим следующие моменты и моментные функции:

Числовое значение найденных моментов:

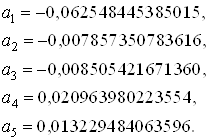
Моментные функции:

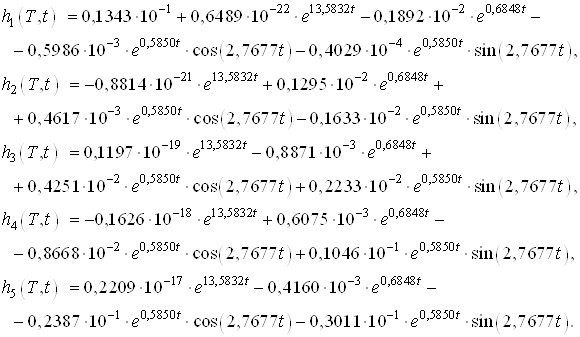
Заметим, что моменты и моментные функции совпадают с моментами и моментными функциями, найденными в пункте (а).

Из этого следует, что функционал, значения , управление и минимальная энергия будут иметь точно такие же числовые значения и аналитические выражения, как и в пункте (3.1).

Оптимальное управление имеет вид:

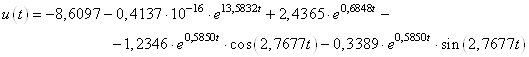
Проверим правильность полученного решения.

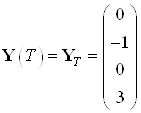
Эталонные значения координат в начальный и конечный момент времени:

,

,

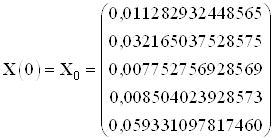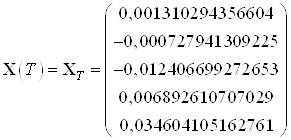
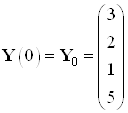Найденные значения координат в начальный и конечный момент времени:

,

,

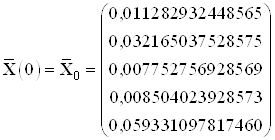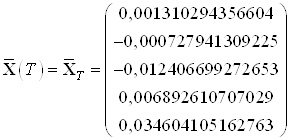
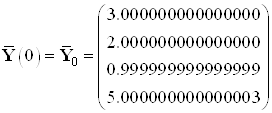Вычислим погрешность полученных результатов:

,

,

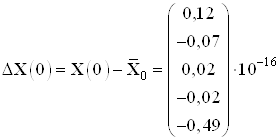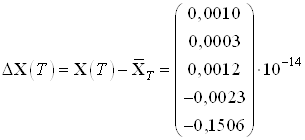
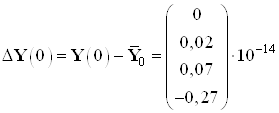Ниже представлены графики полученного решения с помощью скрипта Optimal_L_problem_moments.m.

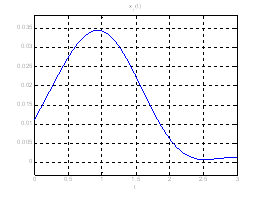
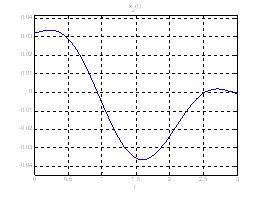
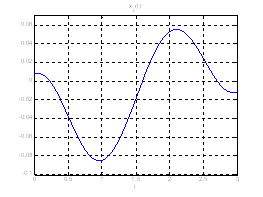
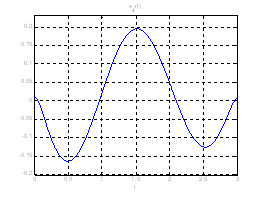
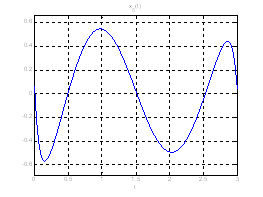
Рис. 18. Графики фазовых координат системы при переходе из  в .

 

 

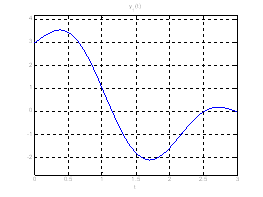
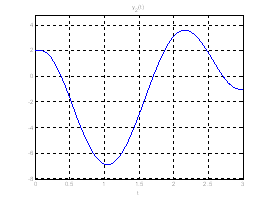
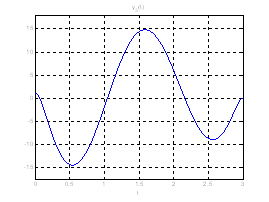
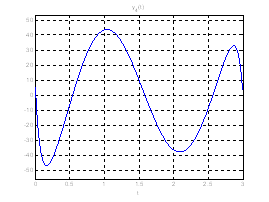
Рис. 19. Графики выходных координат системы при переходе из  в .

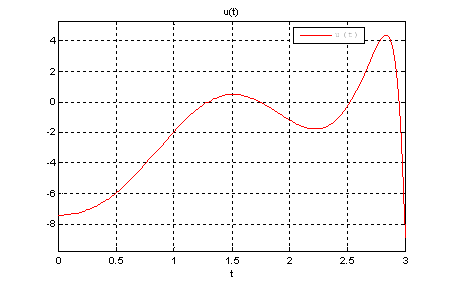
Рис.20. График оптимального управления .

Выводы: Задача перевода системы из начальной точки в конечную с помощью L-проблемы моментов в пространстве состояний и в пространстве вход-выход была решена с точностью до 12-го знака после запятой. Результаты, полученные при переводе системы из начальной точки в конечную, полностью совпадают.

4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)

Система имеет вид:

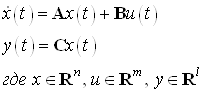
с начальными условиями:

,

.

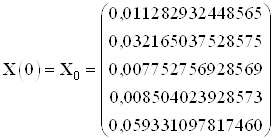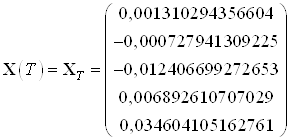
Составим матрицу управляемости и проверим управляемость системы:

.

Составим грамиан управляемости для данной системы:

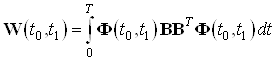
Найдем грамиан по формуле:

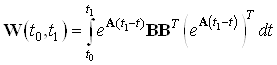
Тогда управление имеет вид:

.

или

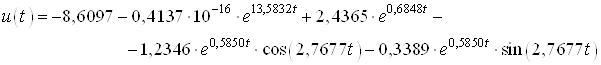
Ниже представлен график оптимального управления полученного с помощью скрипта Gramian_Uprav.m.:

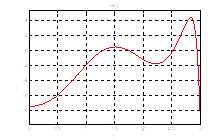
Рис.21. График оптимального управления .

Графики фазовых координат аналогичны, как и в оптимальной L – проблеме моментов.

Сравним управление, полученное в начальной и конечной точках в пунктах 3 и 4 соответственно:

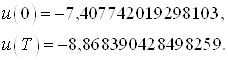 и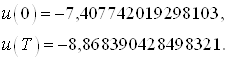

Выводы: Как видно, значения граничных управлений совпадают. А это значит, что задача перевода объекта из начального состояния в конечное решена с высокой степенью точности и с минимальной энергией.

Графическое сравнение оптимальных управлений из пунктов 3 и 4:

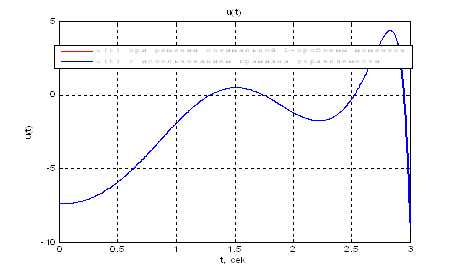
Рис.21. Сравнение графиков оптимального управления .

 

5. Аналитическое конструирование оптимальных регуляторов (АКОР)

5.1 Стабилизации объекта управления на полубесконечном интервале времени

Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме

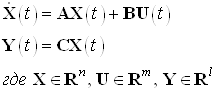
Необходимо получить закон управления

минимизирующий функционал вида

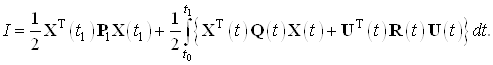
Начальные условия для заданной системы

Моменты времени  фиксированы. Матрицы  — симметричные неотрицательно определенные:

матрица  — положительно определенная:

Матричное дифференциальное уравнение Риккати имеет вид:

Если линейная стационарная система является полностью управляемой и наблюдаемой, то решение уравнения Риккати при  стремится к установившемуся решению  не зависящему от  и определяется следующим алгебраическим уравнением:

В рассматриваемом случае весовые матрицы  и  в функционале не зависят от времени.

Оптимальное значение функционала равно

и является квадратичной функцией от начальных значений отклонения вектора состояния.

Таким образом, получаем, что при  оптимальное управление приобретает форму стационарной обратной связи по состоянию

где  — решение алгебраического матричного уравнения Риккати.

5.1.1. Решение алгебраического уравнения Риккати методом диагонализации

Для решения данной задачи найдем весовые матрицы  и :

Выберем произвольно , тогда

Взяв значения  из решения задачи L – проблемы моментов получим:

Матрицы системы имеют вид:

, .

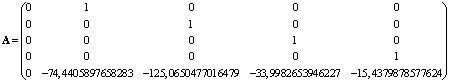
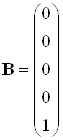Введем расширенный вектор состояния .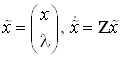

Тогда матрица Z будет иметь следующий вид: ,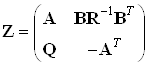

или в численном виде

.

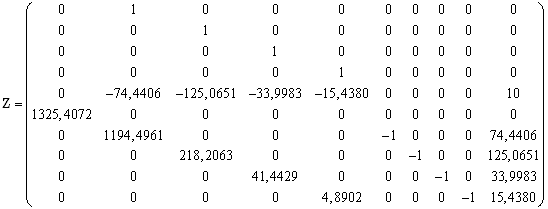Собственные значения матрицы : .

Зная собственные значения и собственные вектора матрицы Z, построим матрицу

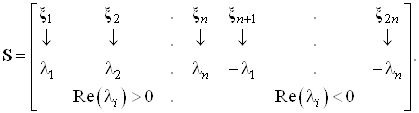
По определению все решения должны быть устойчивы при любых начальных условиях , т.е. при . Чтобы не оперировать комплексными числами, осуществим следующий переход. Пусть:

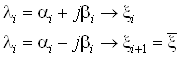
Тогда матрица  формируется следующим образом:

.

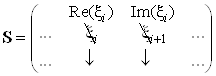Можно показать, что матрицу можно получить из прямой матрицы собственных векторов:

,

.

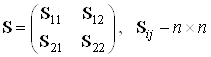Установившееся решение уравнения Риккати, полученное с помощью скрипта Solve_Riccati_Method_Diag.m. имеет вид:

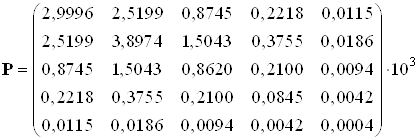
5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния

Весовые матрицы и такие же как и в пункте (5.1.1).

Матрицы  тоже аналогичны.

Запишем уравнение Риккати

.

Зная, что , решаем уравнение методом обратного интегрирования на достаточно большом интервале (примерно 10 с.), получим установившееся решение с помощью скрипта

Solve_Riccati_Method_Revers_Integr.m.:

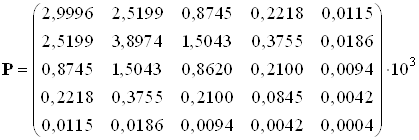
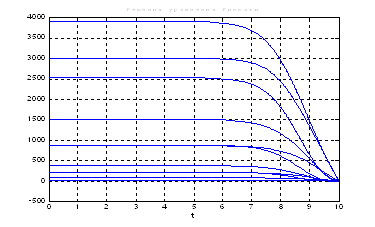
Рис.22. Графики решения уравнения Риккати.

Найдем разницу между решениями уравнения Риккати в пунктах 5.1.1 и 5.1.2:

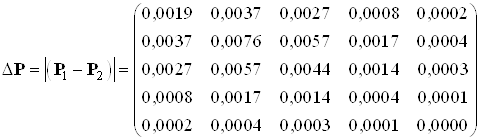
Выводы: сравнивая решения полученные в пунктах 5.1.1 и 5.1.2 можно сказать, что решения уравнения Риккати первым и вторым методами совпадают с заданной точностью. Погрешность расхождения решений невелика.

Используя скрипт AKOR_stabilizaciya_na_polybeskon_interval.m получим коэффициенты регулятора, фазовые координаты системы и управление.

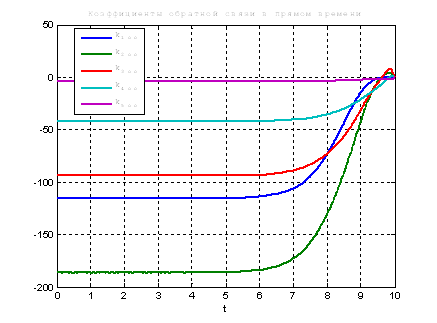
Рис.23. Графики коэффициентов регулятора обратной связи.

 

 

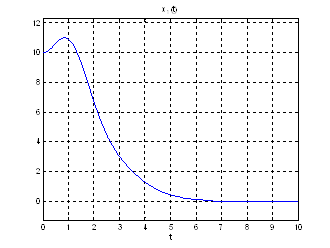
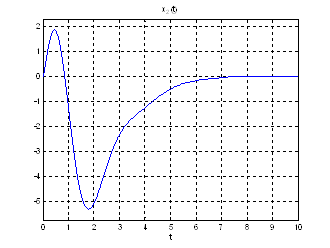
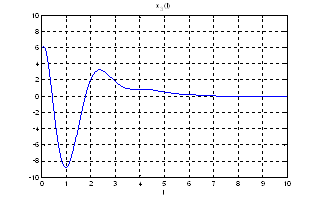
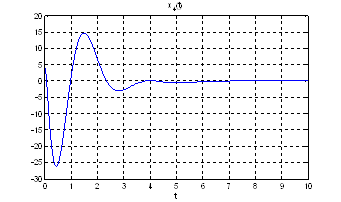
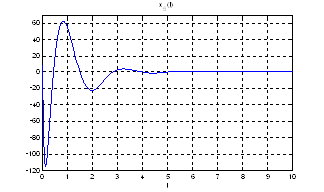
Рис.24. Графики фазовых координат.

Страницы: 1, 2, 3, 4, 5, 6, 7