Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления

Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления

СОДЕРЖАНИЕ

1. Анализ объекта управления

1.1 Анализ линейного стационарного объекта управления, заданного передаточной функцией

1.2 Получение математической модели в пространстве состояний линейного стационарного объекта управления, заданного передаточной функцией

1.2.1 Матрица Фробениуса

1.2.2 Метод параллельной декомпозиции

2. Решение задачи быстродействия симплекс-методом

3. Оптимальная l – проблема моментов

3.1 Оптимальная l – проблема моментов в пространстве «вход-выход»

3.2 Оптимальная l – проблема моментов в пространстве состояний

4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)

5. Аналитическое конструирование оптимальных регуляторов (акор)

5.1 Стабилизации объекта управления на полубесконечном интервале времени

5.1.1 Решение алгебраического уравнения Риккати методом диагонализации

5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния

5.2 Стабилизации объекта управления на конечном интервале времени

5.3 Задача акор – стабилизации для компенсации известного возмущающего воздействия.

5.4 Задача акор для отслеживания известного задающего воздействия. i подход

5.5 Задача акор для отслеживания известного задающего воздействия. ii подход (линейный сервомеханизм)

5.6 Задача акор – слежения со скользящими интервалами.

6. Синтез наблюдателя полного порядка

Литература

Приложение

PlotTimeFrHaract.m

ProstranstvoSostoyanii.m

SimplexMetod2.m

Optimal_L_problem_moments.m

Gramian_Uprav.m       

AKOR_stabilizaciya_na_polybeskon_interval.m

AKOR_stabilizaciya_na_konech_interval.m

Sravnenie_stabilizacii.m

AKOR_stabilizaciya_pri_vozmusheniyah.m

AKOR_slegenie_na_konech_interval_I_podxod.m

AKOR_slegenie_na_konech_interval_II_podxod.m

AKOR_slegenie_so_skolz_intervalami_Modern.m

Sintez_nablyud_polnogo_poryadka.m

Solve_Riccati_Method_Diag.m

Solve_Riccati_Method_Revers_Integr.m

Vozmyshyayushee_Vozdeistvie_Discrete_Revers.m

Zadayushee_Vozdeistvie_Discrete_Revers_Modern.m

1.  Анализ объекта управления

1.1  Анализ линейного стационарного объекта управления, заданного передаточной функцией

Передаточная функция данного объекта имеет вид:

,

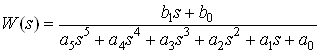где:

, ;

, , , , , .

или

.

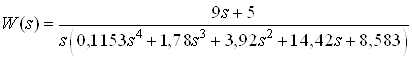Нули передаточной функции:

Полюса передаточной функции (полученные стандартными функциями среды Matlab 7.4):

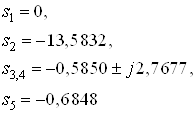
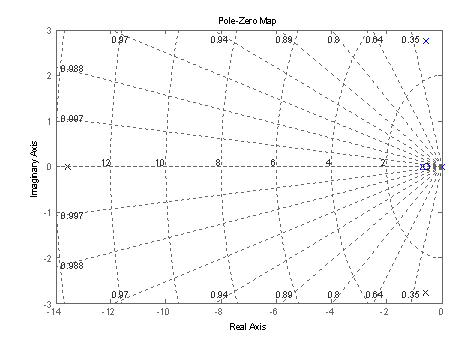
Рис.1. График расположения нулей и полюсов передаточной функции объекта на комплексной плоскости.

Найдем временные характеристики объекта управления.

К временным характеристикам относятся  и .

 – переходная характеристика;

 – импульсная переходная функция;

Для нахождения  и  воспользуемся пакетом Matlab 7.4.

,

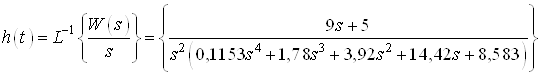Аналитическое выражение для :

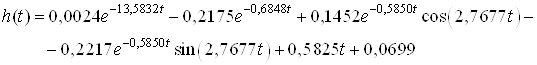
В этом случае  имеет вид

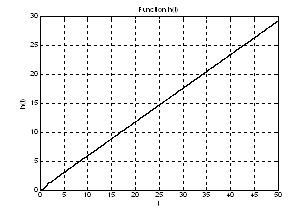
Рис.2. График переходной характеристики .

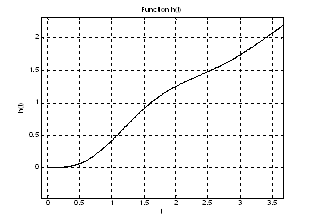
Рис.3. График переходной характеристики  на интервале  (увеличенное).

,

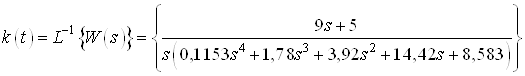Аналитическое выражение для :

.

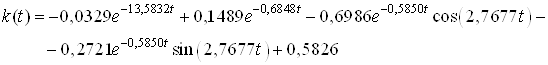В этом случае  имеет вид

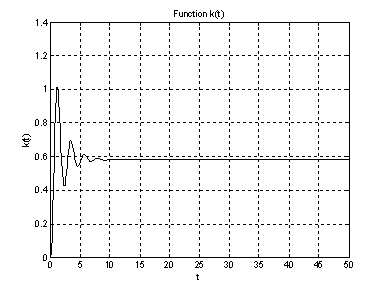
Рис.4. График импульсной переходной характеристики .

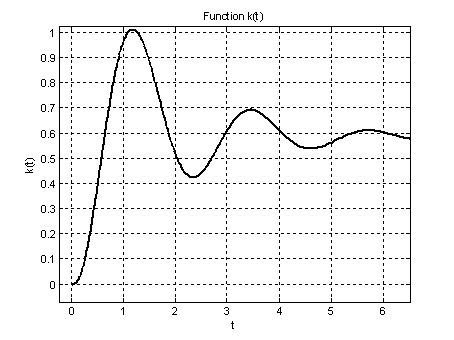
Рис.5. График импульсной переходной характеристики на интервале  (увеличенное).

Найдем частотные характеристики объекта управления.

К частотным характеристикам относятся:

амплитудно – частотная характеристика (АЧХ),

фазо – частотная характеристика (ФЧХ),

амплитудно – фазовая частотная характеристика (АФЧХ),

Аналитическое выражение для АЧХ:

.

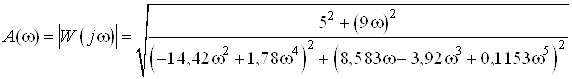В этом случае АЧХ имеет вид

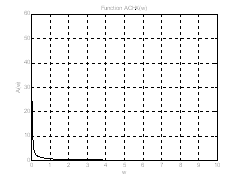
Рис.6. График АЧХ

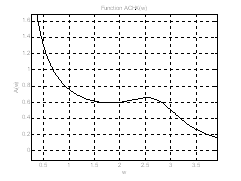
Рис.7. График АЧХ на интервале  (увеличенное). Аналитическое выражение для ФЧХ:

В этом случае ФЧХ имеет вид

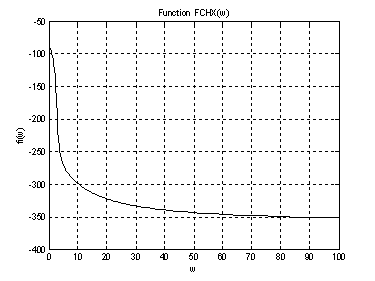
Рис.8. График ФЧХ .

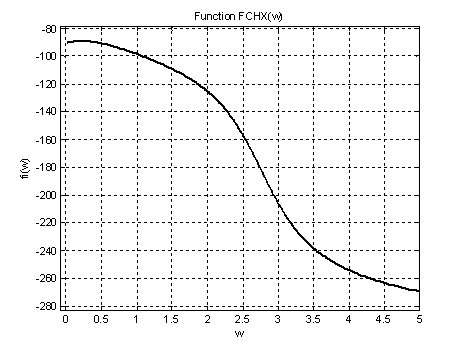
Рис.9. График ФЧХ на интервале  (увеличенное).

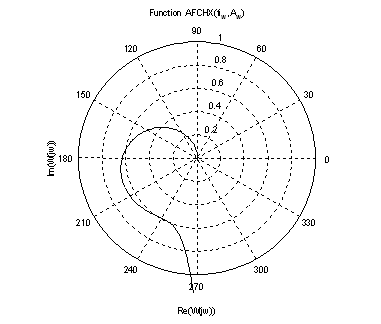
Рис.10. График АФЧХ.

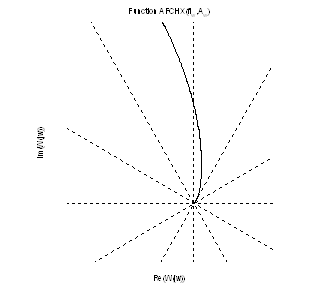
Рис.11. График АФЧХ (увеличенное).

 

Аналитическое выражение для ЛАЧХ:

 

.

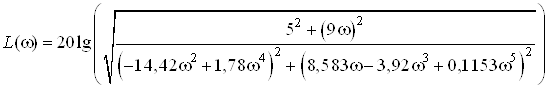В этом случае ЛАЧХ имеет вид

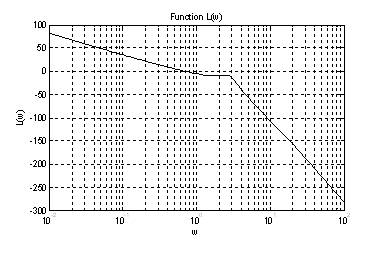
Рис.12. График ЛАЧХ.

Аналитическое выражение для ЛФЧХ:

 

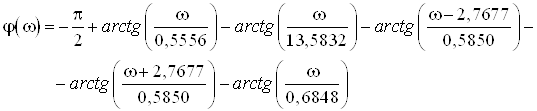
В этом случае ЛФЧХ имеет вид

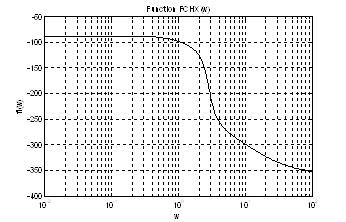
Рис.13. График ЛФЧХ.

1.2 Получение математической модели в пространстве состояний линейного стационарного объекта управления, заданного передаточной функцией

Передаточная функция данного объекта имеет вид:

,

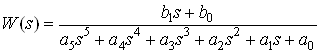где:

, ;

, , , , , .

или

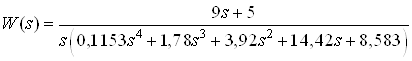
Описание системы в пространстве состояний имеет следующий вид:

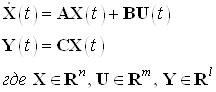
Переходя в область изображений описание системы в пространстве состояний будет иметь следующий вид:

 

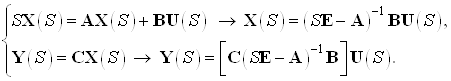
1.2.1 Матрица Фробениуса

Получим выражения, которые определяют вектор состояний и выход заданного объекта в общем виде:

.

.

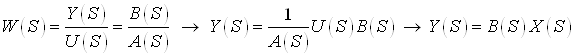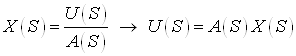Тогда получим:

 (1)

 (2)

Числитель передаточной функции имеет вид: .

Знаменатель передаточной функции:

.

Тогда согласно равенству (1) и (2) имеем

,

.

Перейдем из области изображений в область оригиналов

,

и затем перейдем к нормальной форме Коши

.

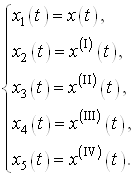
Запишем матрицы состояний

, ,

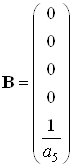Численное значение матриц состояний:

, ,

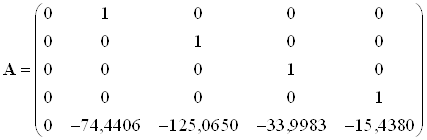1.2.2 Метод параллельной декомпозиции

Запишем передаточную функцию объекта в другом виде, а именно:

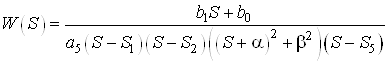
или

.

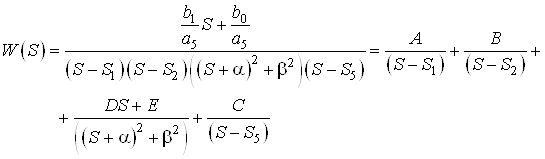Согласно формуле  получим

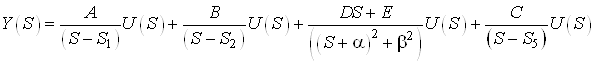
Рассмотрим каждое из слагаемых в отдельности согласно принципу параллельной декомпозиции.

a.  ,

.

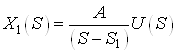b.  ,

.

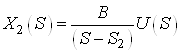c.  ,

,

,

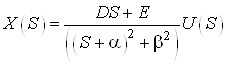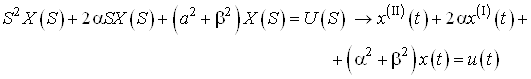
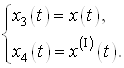
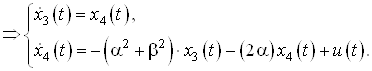
d.  ,

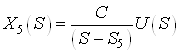Получим выход системы:

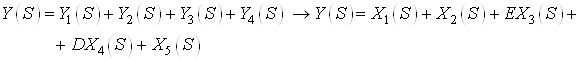
Запишем матрицы состояний

, ,

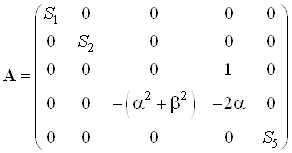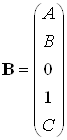Вычисление коэффициентов разложения дробной рациональной функции  на сумму элементарных дробей и проверка правильности получения матриц состояния сделано с помощью пакета Matlab 7.4 (скрипт ProstranstvoSostoyanii.m)

Получены следующие результаты:Матрица СЛАУ:

, ,

,

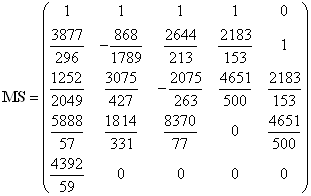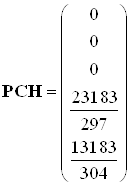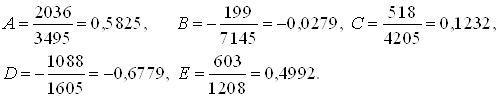
Численное значение матриц состояний:

, ,

.

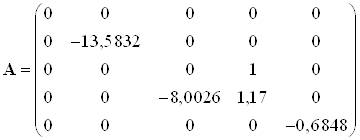2. Решение задачи быстродействия симплекс-методом

Дана система:

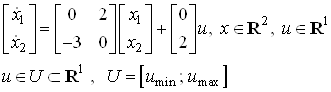 (3)

1. Проверим управляемость данной системы.

Запишем систему ДУ в матричном виде:

,

где .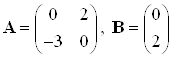

Данная система является стационарной, её порядок , поэтому матрица управляемости имеет вид:

Найдем матрицу управляемости:

Ранг матрицы управляемости равен порядку системы, следовательно, данная система является управляемой.

 следовательно .

Собственные числа матрицы  найдем из уравнения :

        

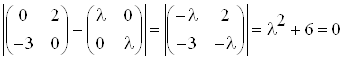
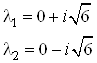
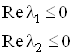
Действительные части собственных значений матрицы  являются неположительными, следовательно, все условия управляемости выполнены.

2. Ссылаясь на решение задачи быстродействия из ДЗ№2 по СУЛА «Решение задачи быстродействия» имеем:

Запишем зависимости , , полученные при решении систем дифференциальных уравнений:

:

:

:

:

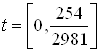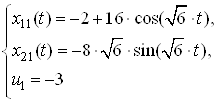
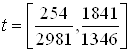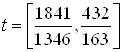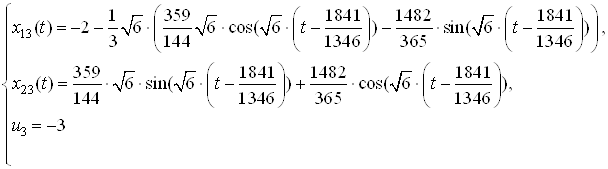
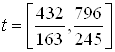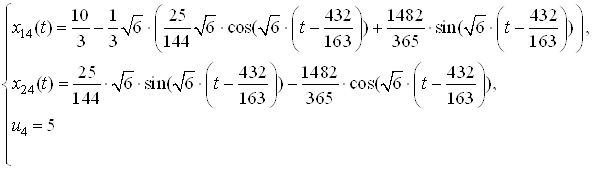
Перейдем к дискретной модели заданной системы. Имеем

 (4)

где  шаг дискретизации и соответствующие матрицы

 (5)

Пусть управление ограничено интервальным ограничением

                 (6)

Тогда на  шаге имеем

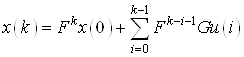         (7)

Известны начальная и конечная точки

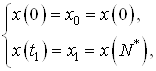
где – оптимальное число шагов в задаче быстродействия.

Решается задача быстродействия

а) Формирование задачи быстродействия как задачи линейного программирования

Конечная точка  в дискретной модели представлена в виде

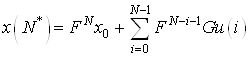        (8)

Получаем  – равенств

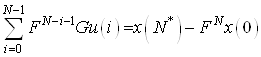     (9)

Для приведения ограничений (9) к канонической форме сделаем необходимое преобразование в правой и левой частях, чтобы правые части были неотрицательными (если правая часть меньше нуля, то домножаем на (-1) левую и правую части). Отметим проведенные изменения точкой в правом верхнем углу соответствующих векторов

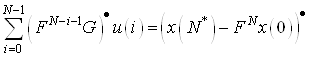. (10)

Для того чтобы получить необходимый допустимый базис для задачи линейного программирования, добавим формально остаточные искусственные переменные (). Таким образом, уравнения (10) представляются в виде

(11)

Так как текущее управление  – управление имеет любой знак,  то сделаем необходимую замену

Тогда уравнения (11) примут вид

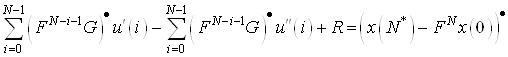(12)

Введем остаточные переменные в ограничения на управление

  (13)

При объединении выражений (12) и (13) получаем  ограничений.

Начальный допустимый базис состоит из остаточных и остаточных искусственных переменных

Формируем целевую функцию (по второму методу выбора начального допустимого базиса)

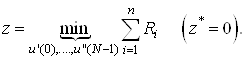 (14)

б) Решение задачи быстродействия

Предположим, что , где – оптимальное число шагов. Так как значение  нам неизвестно (но  известно точно), выбираем некоторое начальное  и решаем задачу линейного программирования (12)-(14).

При этом

Общее число столбцов в симплекс-таблице:  

Число базисных переменных:

Сформируем строку. Имеем

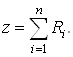
Выразим из уравнения (12) начальные базисные переменные

Страницы: 1, 2, 3, 4, 5, 6, 7