 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Реферат: Методы оценки температурного состояния
В частном случае при описании термоупругости используется квазистационарное приближение, в котором пренебрежено влиянием деформаций на температуру, а в уравнениях движения отброшены члены со второй временной производной. В этом случае уравнение упругости и уравнение теплопроводности решаются фактически раздельно. При этом деформации рассчитываются по известному температурному полю.
Граничные условия на поверхности упругого тела, ограничивающей его объем, состоят из механических и тепловых условий. Механические граничные условия, как и в классической теории упругости, задаются либо в перемещениях, либо в напряжениях. В качестве теплового граничного условия применяется одно из граничных условий теории теплопроводности. Механические и тепловые граничные условия могут быть также смешанными. На одной части поверхности механические граничные условия могут быть заданы в перемещениях, а на другой - в напряжениях. Тепловое граничное условие на одной части поверхности тела задается, например, температурой, а на другой - законом конвективного теплообмена с окружающей средой. Система уравнений, описывающая задачу термоупругости, даже при малых деформациях вследствие нелинейности уравнения теплопроводности является нелинейной [6].
Вместо коэффициентов Ламе часто пользуются другими упругими постоянными для установления связи между напряжениями и дедеформациями. Упругие постоянные выбирают на основе опыта. Обыкновенно на опыте осуществляют простейшие виды напряженного состояния, и те коэффициенты пропорциональности, которые связывают взятый тип напряженного состояния с соответствующим типом деформации, принимают за упругую постоянную. Такие постоянные называют модулями упругости. Соответственно выбранному типу напряженного состояния различают:
1) модуль упругости при растяжении,
2) модуль упругости при сдвиге и 3) модуль упругости при всестороннем сжатии. Может быть установлена зависимость между различно выбранными упругими постоянными. Модули упругости выражаются через коэффициенты Ламе и наоборот.
5. Расчет температурных полей и полей напряжений в оправке при циклическом режиме работы
При моделировании циклического
режима работы прошивной оправки были рассмотрены режимы, приближенные к
реальным условиям эксплуатации оправки на прошивном стане. Рассматривается несвязанная
квазистатическая задача. Модель поведения тела в режиме термонагружения -
упругое тело. Были выбраны две оправки: первая - с диаметром цилиндрического
участка 63 мм, вторая для сравнения - не более 35 мм. В качестве материала была
выбрана высоколегированная сталь с наиболее близкими к стали, из которой
изготавливают прошивные оправки (38ХН3МФА - как один из вариантов), температурными
зависимостями свойств, таких как коэффициент температурного расширения,
коэффициент теплопроводности, модуль нормальной упругости Юнга и удельная
теплоемкость. Для исследования поведения материала в условиях циклического температурного
нагружения важно знать физические свойства исследуемого материала. Физические
свойства стали 38ХН3МФА представлены в таблице 5.1 (по данным источника [7]). Длительность
цикла прошивки принимается равной 22,9 с, из которых 2,9 с затрачивается на
прошивку, а остальные 20 с происходит охлаждение оправки на воздухе либо в воде
в специальном устройстве. Были реализованы оба этих случая. Условия нагрева при
прошивки во всех случаях приняты одинаковыми (температура заготовки ![]() , коэффициент теплопередачи
, коэффициент теплопередачи
![]() ). За время взаимодействия
с нагретой заготовкой оправке передается тепло, вызывающее изменение ее
температурного поля. Вместе с этим меняется и поле напряжений. За время
охлаждения оправка не успевает отдать все накопленное тепло и при следующем
цикле нагрева значения температур на внутренних температурных слоях будут выше.
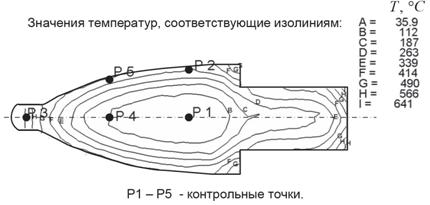
Это различие в температурах наружной поверхности и внутри оправки отчетливо
видно по изолиниям температур, показанным на рис.5.1. Более массивная часть
оправки с большим диаметром нагревается дольше и также медленнее и отдает тепло.
Циклический режим работы создает нестационарное поле температур, поэтому
наблюдаемая на рисунке картина теплового поля, зафиксированная в некоторый
момент времени, непрерывно меняется, и в каждый момент времени будет различной.
На этом же рисунке отмечены положения контрольных точек, для которых приведены
графики изменения температур и температурных напряжений. Рассмотренные режимы
работы оправки и номера соответствующих рисунков приведены в таблице 5.2.
). За время взаимодействия
с нагретой заготовкой оправке передается тепло, вызывающее изменение ее
температурного поля. Вместе с этим меняется и поле напряжений. За время
охлаждения оправка не успевает отдать все накопленное тепло и при следующем
цикле нагрева значения температур на внутренних температурных слоях будут выше.
Это различие в температурах наружной поверхности и внутри оправки отчетливо
видно по изолиниям температур, показанным на рис.5.1. Более массивная часть
оправки с большим диаметром нагревается дольше и также медленнее и отдает тепло.
Циклический режим работы создает нестационарное поле температур, поэтому
наблюдаемая на рисунке картина теплового поля, зафиксированная в некоторый
момент времени, непрерывно меняется, и в каждый момент времени будет различной.
На этом же рисунке отмечены положения контрольных точек, для которых приведены
графики изменения температур и температурных напряжений. Рассмотренные режимы
работы оправки и номера соответствующих рисунков приведены в таблице 5.2.
Таблица 5.1. Физические свойства стали марки 38ХН3МФА.
|
Температура испытания, |
20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
|
Модуль нормальной упругости |
2,10 | 2,03 | 1,97 | 1,90 | 1,84 | 1,76 | 1,70 | 1,54 | 1,37 | н. д. |
|
Плотность |
7900 | |||||||||
|
Коэффициент теплопроводности |
34 | 34 | 34 | 33 | 32 | 32 | 30 | 29 | 28 | н. д. |
|
Уд. электросопротивление |
300 | 321 | 365 | 437 | 516 | 613 | 750 | 897 | 1080 | н. д. |
|
Температура испытания, |
20 - 100 |
20 - 200 |
20 - 300 |
20 - 400 |
20 - 500 |
20 - 600 |
20 - 700 |
20 - 800 |
20 - 900 |
20 - 1000 |
|
Коэффициент линейного расширения |
12,0 | 12,5 | 12,9 | 13,3 | 13,6 | 13,8 | 13,8 | 10,7 | н. д. | н. д. |
|
Удельная теплоемкость |
496 | 508 | 525 | 538 | 567 | 601 | 672 | 697 | н. д. | н. д. |
Зарубежный ближайший аналог материала 38ХН3МФА: DIN, WNr 34NiCrMoV14-5.
Таблица 5.2. Рассмотренные режимы работы оправки и номера рисунков к ним.
| Диаметр оправки | Режим работы | Исследуемый параметр | Номер рисунка |
| 63 мм | Нагрев - охлаждение на воздухе | Температурное поле | 5.1 |
| Поле средних напряжений | 5.2 | ||
| Температуры в точках | 5.3 | ||
| Средние напряжения в точках | 5.4 | ||
| Нагрев - охлаждение в воде | Температуры в точках | 5.5 | |
| Средние напряжения в точках | 5.6 | ||
| Предварительный нагрев -нагрев - охлаждение на воздухе | Температуры в точках | 5.7 | |
| Средние напряжения в точках | 5.8 | ||
| 35 мм | Нагрев - охлаждение на воздухе | Температурное поле | 5.9 |
| Поле средних напряжений | 5.10 | ||
| Температуры в точках | 5.11 | ||
| Средние напряжения в точках | 5.12 |
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |