 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Реферат: Методы оценки температурного состояния
где ![]() ,
,
![]() и
и ![]() - площади поверхностей
контакта металла с валками, линейками и окружающей средой;
- площади поверхностей
контакта металла с валками, линейками и окружающей средой; ![]() ,
, ![]() ,
, ![]() ,
, ![]() - плотности тепловых
потоков;
- плотности тепловых
потоков; ![]() - плотность потока
тепловых потерь в окружающую среду;
- плотность потока
тепловых потерь в окружающую среду; ![]() и
и ![]() - плотности потоков
тепловых потерь к валкам и линейкам рассчитываются при допущении
квазистационарного режима теплопроводности с учетом температурного
сопротивления слоя окалины:
- плотности потоков
тепловых потерь к валкам и линейкам рассчитываются при допущении
квазистационарного режима теплопроводности с учетом температурного
сопротивления слоя окалины:
![]() ,(2.19)
,(2.19)
где ![]() и
и
![]() - температура валков и
линеек в стационарном режиме работы.
- температура валков и
линеек в стационарном режиме работы.
Кондуктивный теплообмен между металлом и оправкой через слой окалины в месте контакта или через воздушный зазор, в первом приближении, рассчитывается при допущении квазистационарного режима теплообмена.
Через слой окалины:
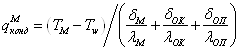 ; (2.20)
; (2.20)
через воздушный зазор:
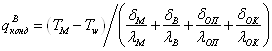 ,(2.21)
,(2.21)
где ![]() -
средняя температура металла при прошивке;
-
средняя температура металла при прошивке; ![]() -
температура поверхности оправки;
-
температура поверхности оправки; ![]() ,
, ![]() - толщина приграничного
слоя металла и оправки;
- толщина приграничного
слоя металла и оправки; ![]() ,
, ![]() - толщина окалины и
воздушной прослойки;
- толщина окалины и
воздушной прослойки; ![]() ,
, ![]() ,
, ![]() ,
, ![]() - коэффициенты
теплопроводности деформируемого металла, оправки, окалины и воздуха
соответственно.
- коэффициенты
теплопроводности деформируемого металла, оправки, окалины и воздуха
соответственно.
Плотность лучистого теплового потока в воздушном зазоре находится при допущении равенства поверхностей, расположенных по обе стороны зазора. Учитывая, что воздух является диатермичной средой, получим
![]() ,(2.22)
,(2.22)
где ![]() -
постоянная Стефана - Больцмана;
-
постоянная Стефана - Больцмана; ![]() - приведенная
степень черноты. Плотность теплового потока, выделяемого при работе сил трения,
определяется по формуле:
- приведенная
степень черноты. Плотность теплового потока, выделяемого при работе сил трения,
определяется по формуле:
![]() ,(2.23)
,(2.23)
где ![]() -
касательное напряжение трения;
-
касательное напряжение трения; ![]() - скорость
перемещения металла вдоль оси оправки (оси Oz).
- скорость
перемещения металла вдоль оси оправки (оси Oz).
Касательное напряжение трения рассчитывается по формуле
![]() ,(2.24)
,(2.24)
в которой ![]() - коэффициент трения; Р
- сила нормального давления на оправку.
- коэффициент трения; Р
- сила нормального давления на оправку.
Для конических оправок различных геометрических размеров значения давлений, сохраняются на носке, в конце сферической части, в пережиме и в конце третьего участка.
Скорость течения металла в рассматриваемом расчетном сечении находится из уравнения неразрывности, которое при некотором допущении имеет вид:
![]() ,(2.25)
,(2.25)
где ![]() -
средняя скорость перемещения металла в сечении
-
средняя скорость перемещения металла в сечении ![]() между
валком и оправкой;
между
валком и оправкой; ![]() - скорость
движения гильзы на выходе из зазора. Скорость выхода гильзы определена
экспериментально в зависимости от угла подачи
- скорость
движения гильзы на выходе из зазора. Скорость выхода гильзы определена
экспериментально в зависимости от угла подачи ![]() .
.
Величина деформационного
разогрева ![]() зависит не только от величины
внутренних тепловыделений при деформации, но и от интенсивности теплообмена с
окружающей средой и технологическим инструментом, поэтому для ее определения
необходимо применить метод итераций. В качестве первого приближения
зависит не только от величины
внутренних тепловыделений при деформации, но и от интенсивности теплообмена с
окружающей средой и технологическим инструментом, поэтому для ее определения
необходимо применить метод итераций. В качестве первого приближения ![]() рассчитывается при
допущении равенства нулю тепловых потоков
рассчитывается при
допущении равенства нулю тепловых потоков ![]() и
и
![]() .
.
Условия на границе металл - окалина.
Окалинообразующий слой очень
существенно влияет на температурное поле оправки. Теплофизические свойства
окалины характеризуются коэффициентом теплопроводности окалины ![]() . На границе металл-окалина
за счет действия сил трения происходит выделение теплоты. Между слоем окалины и
оправкой происходит кондуктивный теплообмен (теплопроводностью). Между слоем
окалины и металлом осуществляется как кондуктивный теплообмен, так и лучистый
теплообмен через воздушную среду, заполняющую прослойку. При этом воздух
считается диатермической средой, то есть прозрачной для лучистой энергии. Теплофизические
свойства воздуха характеризуются коэффициентом теплопроводности воздуха
. На границе металл-окалина
за счет действия сил трения происходит выделение теплоты. Между слоем окалины и
оправкой происходит кондуктивный теплообмен (теплопроводностью). Между слоем
окалины и металлом осуществляется как кондуктивный теплообмен, так и лучистый
теплообмен через воздушную среду, заполняющую прослойку. При этом воздух
считается диатермической средой, то есть прозрачной для лучистой энергии. Теплофизические
свойства воздуха характеризуются коэффициентом теплопроводности воздуха ![]() .
.
Начальные (временные) условия.
Рассматриваемый процесс является нестационарным, то есть в уравнения входит время в качестве переменной. Для такого процесса необходимы начальные условия, которые состоят в задании закона распределения температуры внутри тела в начальный момент времени.
При первой прошивке начальное
поле температур задается равномерным и равным температуре окружающей среды ![]() :
:
![]() .
(2.26)
.
(2.26)
При охлаждении оправки в качестве начального условия принимается температурное поле, полученное в конце нагрева оправки (в конце прошивки):
![]() .
(2.27)
.
(2.27)
Для второго и последующих циклов нагрева и охлаждения за начальное условие также принимается температурное поле предыдущего процесса теплообмена.
Граничные условия (на границе в нерегулярных узлах).
Применяются условия второго рода
(условия Неймана): на поверхности задается плотность теплового потока как
функция от температуры и координаты ![]() .
.
Граничные условия на границе металл - оправка при нагреве.
Граничные условия в области раздела деформируемый металл - оправка задаются через плотность теплового потока с учетом теплоты, выделяемой при работе сил трения и температурного сопротивления слоя окалины:
![]() ; (2.28)
; (2.28)
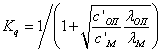 ,(2.29)
,(2.29)
где ![]() -
плотность кондуктивного теплового потока в системе металл - окалина - заготовка;
-
плотность кондуктивного теплового потока в системе металл - окалина - заготовка;
![]() -
плотность кондуктивного теплового потока в системе металл - воздух - оправка;
-
плотность кондуктивного теплового потока в системе металл - воздух - оправка;
![]() -
плотность лучистого теплового потока от металла к оправке в воздушном зазоре;
-
плотность лучистого теплового потока от металла к оправке в воздушном зазоре;
![]() -
коэффициент контакта, равный отношению площади контакта ко всей площади
поверхности оправки в данном сечении и определяемый экспериментально (в нашем
случае на I участке
-
коэффициент контакта, равный отношению площади контакта ко всей площади
поверхности оправки в данном сечении и определяемый экспериментально (в нашем
случае на I участке ![]() , на II участке 0
<
, на II участке 0
< ![]() < 1 (
< 1 (![]() ), а на III и IV участках -
), а на III и IV участках -
![]() );
); ![]() - плотность теплового
потока за счет сил трения;
- плотность теплового
потока за счет сил трения; ![]() - коэффициент,
учитывающий долю теплоты, поступающей на оправку
- коэффициент,
учитывающий долю теплоты, поступающей на оправку
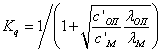 . (2.30)
. (2.30)
Граничные условия при охлаждении оправки (граничные условия третьего рода).
При расчете охлаждения оправки
между прошивками применяются граничные условия третьего рода (используется
температура окружающей среды ![]() и
коэффициент теплоотдачи
и
коэффициент теплоотдачи ![]() ):
):
![]() . (2.31)
. (2.31)
![]() -
плотность теплового потока с поверхности оправки при охлаждении, которая
рассчитывается в зависимости от условий охлаждения. Например, при охлаждении на
воздухе:
-
плотность теплового потока с поверхности оправки при охлаждении, которая
рассчитывается в зависимости от условий охлаждения. Например, при охлаждении на
воздухе:
![]() ,(2.32)
,(2.32)
где ![]() -
коэффициент теплоотдачи свободной конвекцией;
-
коэффициент теплоотдачи свободной конвекцией; ![]() -
температура поверхности оправки;
-
температура поверхности оправки; ![]() - температура
охлаждающей среды (в данном случае воздуха).
- температура
охлаждающей среды (в данном случае воздуха).
При интенсивном охлаждении оправки
![]() .
(2.33)
.
(2.33)
В этом случае ![]() - коэффициент теплоотдачи
при вынужденной конвекции от поверхности оправки к потоку охладителя. Расчет
коэффициента теплоотдачи выполняется по известным критериальным зависимостям.
- коэффициент теплоотдачи
при вынужденной конвекции от поверхности оправки к потоку охладителя. Расчет
коэффициента теплоотдачи выполняется по известным критериальным зависимостям.
Граничные условия на четвертом участке.
Граничные условия вдоль оси Oz на четвертом участке задаются при допущении отсутствия теплообмена на этой границе:
![]() .
(2.34)
.
(2.34)
2.2 Математическая формулировка задачи расчета температурного поля оправки
В общем виде уравнение теплопроводности записывается так:
![]() ,(2.35)
,(2.35)
где ![]() -
температура,
-
температура, ![]() - теплоемкость удельная
массовая теплоемкость,
- теплоемкость удельная
массовая теплоемкость, ![]() - коэффициент
теплопроводности и
- коэффициент
теплопроводности и ![]() - плотность
источников тепла.
- плотность
источников тепла.
Поскольку внутренних источников тепла нет, то уравнение записывается так:
![]() . (2.36)
. (2.36)
Поскольку прошивная оправка представляет собой тело вращения, то удобно использовать цилиндрическую систему координат. На первом участке для повышения точности решения применена сферическая система координат. Уравнение теплопроводности для сферической системы координат (участок I):
![]() . (2.37)
. (2.37)
Для цилиндрической системы координат (участки II, III и IV):
![]() . (2.38)
. (2.38)
В уравнениях ![]() - цилиндрические
координаты;
- цилиндрические
координаты; ![]() - сферические координаты;
- сферические координаты; ![]() - температура;
- температура; ![]() - время;
- время; ![]() - удельная объемная
теплоемкость;
- удельная объемная
теплоемкость; ![]() - плотность
материала оправки;
- плотность
материала оправки; ![]() - удельная
массовая теплоемкость.
- удельная
массовая теплоемкость.
Для центра сферы уравнение теплопроводности записывается следующим образом:
![]() . (2.39)
. (2.39)
Для оси центра:
![]() . (2.40)
. (2.40)
Для выделения единственного решения дифференциального уравнения применяются описанные выше условия однозначности [3], [4].
3. Метод и алгоритм решения уравнений теплообмена
Для решения дифференциального
уравнения теплопроводности (2.36) с соответствующими начальными и граничными
условиями применяется метод конечных разностей. Конечно-разностная сетка
изображена на рис.3.1 Каждый узел сетки нумеруется в виде ![]() , где
, где ![]() - номер узла по
направлению
- номер узла по
направлению ![]() для полусферы и
цилиндра, a
для полусферы и
цилиндра, a ![]() - номер узла по
направлению
- номер узла по
направлению ![]() для полусферы и по
направлению
для полусферы и по
направлению ![]() для цилиндра. Нумерация
узлов начинается от центра сферы и оси цилиндра. Коническая поверхность оправки
заменена ступенчатой, кратной шагу
для цилиндра. Нумерация
узлов начинается от центра сферы и оси цилиндра. Коническая поверхность оправки
заменена ступенчатой, кратной шагу ![]() . Дискретные
моменты времени обычно нумеруются индексами:
. Дискретные
моменты времени обычно нумеруются индексами: ![]() -
предыдущий, а
-
предыдущий, а ![]() - последующий
моменты времени. Номер предыдущей и последующей итерации обозначается верхними
индексами
- последующий
моменты времени. Номер предыдущей и последующей итерации обозначается верхними
индексами ![]() и
и ![]() соответственно.
соответственно.
Для аппроксимации
дифференциальных уравнений теплопроводности (2.37) - (2.40) применяется неявная
консервативная итерационная разностная схема, реализуемая методом Гаусса-Зейделя.
Суть этого метода заключается в том, что при расчете температуры ![]() в узле
в узле ![]() на
на ![]() -й итерации используются температуры
-й итерации используются температуры
![]() и
и ![]() из предыдущей итерации и
вновь вычисленные температуры
из предыдущей итерации и
вновь вычисленные температуры ![]() и
и ![]() на расчетной
на расчетной ![]() -й итерации. Неявность
разностной схемы достигается применением итерационной процедуры на каждом
временном слое.
-й итерации. Неявность
разностной схемы достигается применением итерационной процедуры на каждом
временном слое.
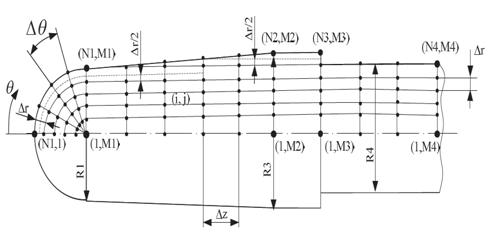
Рис.3.1 Конечно-разностная сетка, применяемая в численном методе конечных разностей при решении задачи теплопроводности оправки.
Конечно-разностные аналоги дифференциального уравнения теплопроводности для всех характерных участков оправки записываются так:
а) внутренние узлы сферы ![]() :
:
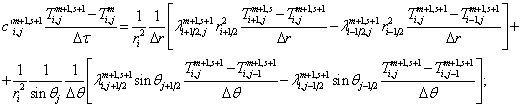 (3.1)
(3.1)
б) внутренние узлы конической и
цилиндрической частей оправки ![]() :
:
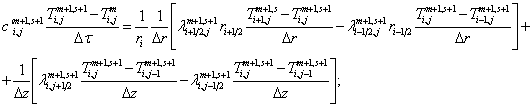 (3.2)
(3.2)
в) температура в узлах,
расположенных на поверхности сопряжения: полусфера - конус, рассчитывается
следующим образом. Поскольку поверхность сопряжения одновременно принадлежит
полусфере и конусу, то вторая производную по координатам ![]() и
и ![]() аппроксимируется по
формулам, приведенным далее. Для полусферы принимается составляющая второй
производной по углу
аппроксимируется по
формулам, приведенным далее. Для полусферы принимается составляющая второй
производной по углу ![]() в сферических
координатах, а для конической части - составляющая второй производной по
в сферических
координатах, а для конической части - составляющая второй производной по ![]() в цилиндрических
координатах. Узлы, расположенные на поверхности сопряжения полусфера - конус,
пронумерованы
в цилиндрических
координатах. Узлы, расположенные на поверхности сопряжения полусфера - конус,
пронумерованы ![]() . На поверхности
сопряжения при использовании равномерной сетки уравнения записываются так:
. На поверхности
сопряжения при использовании равномерной сетки уравнения записываются так:
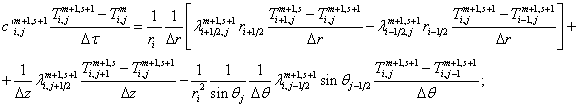 (3.3)
(3.3)
г) узлы, расположенные на оси
полусферы ![]()
 (3.4)
(3.4)
д) узлы, расположенные на оси
конической и цилиндрической частей оправки ![]()
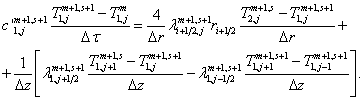 (3.5)
(3.5)
При аппроксимации
дифференциальных уравнений (2.39) и (2.40) конечно-разностными аналогами (3.3) и
(3.4) учитывается, что в силу симметрии ![]() и
и
![]() . В вышеприведенных
формулах (3.1) - (3.4) принимаются следующие обозначения:
. В вышеприведенных
формулах (3.1) - (3.4) принимаются следующие обозначения:
![]() ;
(3.6)
;
(3.6)
![]() ;
(3.7)
;
(3.7)
![]() ;
(3.8)
;
(3.8)
![]() ;
(3.9)
;
(3.9)
![]() ,(3.10)
,(3.10)
где ![]() -
шаг по координате
-
шаг по координате ![]() .
.
На поверхности оправки граничные
условия II рода при нагреве (2.28) и охлаждении (2.31) аппроксимируются по трем
приграничным узлам с учетом поглощения (выделения) теплоты в приграничном узле
толщиной ![]() :
:
![]() ,(3.11)
,(3.11)
где ![]() -
плотность теплового потока, поступающего на оправку при прошивке или уходящего
с нее при охлаждении. Из последнего уравнения получается формула для
определения температуры поверхности оправки в узлах
-
плотность теплового потока, поступающего на оправку при прошивке или уходящего
с нее при охлаждении. Из последнего уравнения получается формула для
определения температуры поверхности оправки в узлах ![]() :
:
 . (3.12)
. (3.12)
Граничное условие (2.58) на
торцевой границе стержня также аппроксимируется по значениям температуры в трех
приграничных узлах сетки ![]()
![]() ,(3.13)
,(3.13)
откуда получается
![]() .
(3.14)
.
(3.14)
При расчете температуры в "центральной"
точке сферы и усеченного конуса ![]() возникают
трудности, связанные с тем, что эта точка принадлежит одновременно центру
полусферы и оси плоскости сопряжения полусфера - цилиндр. Температура в этой
"центральной" точке определяется по балансу тепловой энергии в
объеме, прилегающем к этой точке (рис.3.2):
возникают
трудности, связанные с тем, что эта точка принадлежит одновременно центру
полусферы и оси плоскости сопряжения полусфера - цилиндр. Температура в этой
"центральной" точке определяется по балансу тепловой энергии в
объеме, прилегающем к этой точке (рис.3.2):
![]() ,(3.15)
,(3.15)
где ![]() -
удельная объемная теплоемкость;
-
удельная объемная теплоемкость; ![]() - объем
тела вращения ABDSA;
- объем
тела вращения ABDSA; ![]() - тепловой
поток, поступающий в выделенный объем
- тепловой
поток, поступающий в выделенный объем![]() .
.
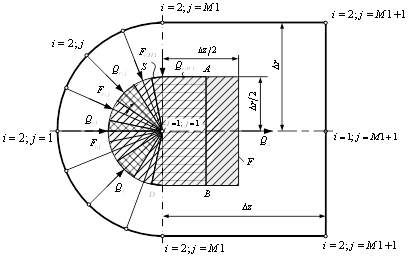
Рис.3.2 Пояснение к расчету температурного поля в центре сферического участка.
Тепловой поток равен
![]() ,(3.16)
,(3.16)
где составляющие теплового баланса определяются по формулам
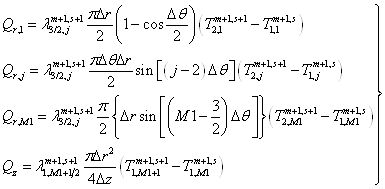 . (3.17)
. (3.17)
Объем тела вращения ABDSA (см. рис.3.2) рассчитывается по формуле
![]() . (3.18)
. (3.18)
В общем случае все конечно-разностные уравнения приводятся к виду:
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |