Курсовая работа: Построение модели поведения потребителя в условиях совершенной конкуренции

Построим модель для третьего потребителя. Будем варьировать коэффициенты предпочтительности благ (0,45 и 0,4). Модель представлена в табл. 4

Табл. 4

x1	x2	b1	b2	p1	p2	S	p1*x1	p2*x2	R	b1+b2	p1*x1+p2*x2
19,85	23,53	0,45	0,4	20	15	13,57	397,06	352,94	750	0,85	750,00
19,85	22,06	0,45	0,4	20	16	13,23	397,06	352,94	750	0,85	750,00
19,85	20,76	0,45	0,4	20	17	12,91	397,06	352,94	750	0,85	750,00
19,85	19,61	0,45	0,4	20	18	12,62	397,06	352,94	750	0,85	750,00
19,85	18,58	0,45	0,4	20	19	12,35	397,06	352,94	750	0,85	750,00
19,85	17,65	0,45	0,4	20	20	12,10	397,06	352,94	750	0,85	750,00
19,85	16,81	0,45	0,4	20	21	11,86	397,06	352,94	750	0,85	750,00
18,05	23,53	0,45	0,4	22	15	13,00	397,06	352,94	750	0,85	750,00
18,05	22,06	0,45	0,4	22	16	12,67	397,06	352,94	750	0,85	750,00
18,05	20,76	0,45	0,4	22	17	12,37	397,06	352,94	750	0,85	750,00
18,05	19,61	0,45	0,4	22	18	12,09	397,06	352,94	750	0,85	750,00
18,05	18,58	0,45	0,4	22	19	11,83	397,06	352,94	750	0,85	750,00
18,05	17,65	0,45	0,4	22	20	11,59	397,06	352,94	750	0,85	750,00
18,05	16,81	0,45	0,4	22	21	11,37	397,06	352,94	750	0,85	750,00
16,54	23,53	0,45	0,4	24	15	12,50	397,06	352,94	750	0,85	750,00
16,54	22,06	0,45	0,4	24	16	12,18	397,06	352,94	750	0,85	750,00
16,54	20,76	0,45	0,4	24	17	11,89	397,06	352,94	750	0,85	750,00
16,54	19,61	0,45	0,4	24	18	11,62	397,06	352,94	750	0,85	750,00
16,54	18,58	0,45	0,4	24	19	11,38	397,06	352,94	750	0,85	750,00
16,54	17,65	0,45	0,4	24	20	11,14	397,06	352,94	750	0,85	750,00
16,54	16,81	0,45	0,4	24	21	10,93	397,06	352,94	750	0,85	750,00

По этой модели также видна зависимость, которая показывает уменьшение количества потребления первого блага от изменения цены на него и уменьшение количества второго при увеличении цены на него.

5. Результаты исследования экономико-математической модели и анализ получения результатов

Для того чтобы сделать вывод, о том как изменяются параметры модели, а с ними и поведение потребителя с помощью графиков покажем зависимость количества блага от изменения уровня цен.

На рисунке 3 показана зависимость количества первого и второго блага от цены второго.

При R=750, p1=20

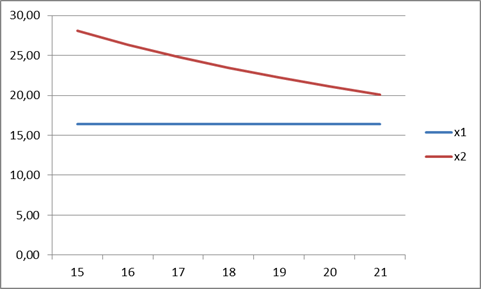
Рис. 3

При увеличении цены на второе благо, его количество потребления уменьшается. Если цена на второе благо постоянна, то количество потребления его не изменяется.

Рисунок 4 отображает изменение цены первого блага на две единицы, при неизменной цене второго блага.

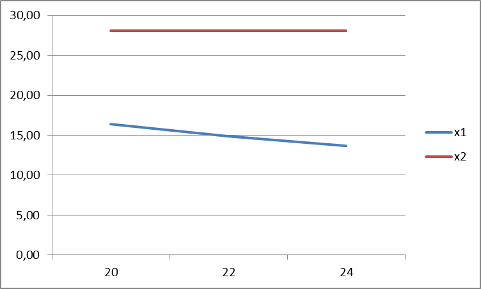
Рис. 4

При увеличении цены на первое благо, его количество потребления уменьшается. Цена на второе благо постоянна, значит количество потребления его не изменяется.

На рис. 5 показана зависимость количества первого и второго блага от цены второго.

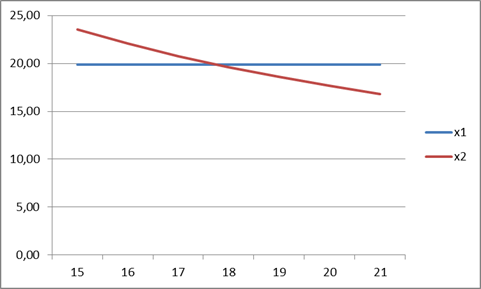
Рис. 5

Необходимо отметить, что при изменении цен на благо уменьшается и функция полезности потребителя, то есть при увеличении цены на благо потребитель не будет склонен к его приобретению.

Выводы

В данной курсовой работе был проведен многофакторный анализ поведения потребителя в зависимости от изменения различных факторов, таких как: цена на первое благо, цена на второе благо и уровня предпочтительности.

Сам анализ проводился с помощью средств Excel. Модель представлена в следующем виде: , которая отвечает всем необходимым требованиям, представленным в ходе курсовой работы.

Оптимальным решением является набор благ, состоящий из 16,4 единиц первого блага по цене 20 ден. ед. и 28,12 единиц второго блага по цене 15 ден. ед. при доходе 750 ден. ед. При котором функция полезности составляет 11,95.

Список использованной литературы

1 Конспект лекций по курсу «Моделирование экономики» для студентов специальности «Экономическая кибернетика» Составитель А.Б.Алёхин – Одесса: ОНПУ, 2003. – 60с.

2 Савицкая В. Е. Курс лекций по микроэкономике. М. 2002,- 248с.

3 Б. С. Малышев Теория предельной полезности (потребитель на рынке товаров и услуг): Учебное пособие / Харьковский гос. Ун. – Харьков, 1999 -40с.

4 М. Интрилигатор. Математические методы оптимизации и экономическая теория. М., Прогресс, 1975.-606 с.

5 Экономическая кибернетика. Сб. задач под редакцией Б. Б. Бухарева. Киев, 1998.