Курсовая работа: Построение модели поведения потребителя в условиях совершенной конкуренции

Курсовая работа

по дисциплине: «Моделирование экономики»

на тему: «Построение модели поведения потребителя в условиях совершенной конкуренции»

Аннотация

При написании курсовой работы была использована и построена формализованная теория поведения потребителя для случая двух частично взаимозаменяемых благ с нелинейной функцией полезности. В ходе работы была разработана математическая модель потребления. В модели изменению поддавались ценовые конъюнктуры и предпочтительности благ потребителя, с помощью чего были исследованы свойства модели и изучены закономерности поведения потребителя.

Анализ модели проводился с помощью пакета MS Excel.

Содержание

Введение. 4

1. Экономическая постановка задачи и характеристика объекта. 5

2. Математическая постановка модели поведения потребителя. 7

2.1 Математическая постановка задачи поведения потребителя. 7

2.2 Обоснование выбора модели поведения потребителя. 9

3. Метод и алгоритм анализа модели. 11

4 Программная реализация экономико-математической модели и метода ее анализа 14

5. Результаты исследования экономико-математической модели и анализ получения результатов. 18

Выводы.. 21

Список использованной литературы.. 22

Введение

Теория потребления выбора дает возможность изучить принципы построения спроса на определенные товары и услуги. При изучения теории надо помнить, что рассматривая область в целом требуется ее разделить на составные части и их подробно, по отдельности изучить. В курсовой работе изучаеться склонность человека к конкретному товару среди множества на рынке.

Целью курсовой работы является наработка опыта по изучению методов и приемов построения и анализа математических моделей различных экономических объектов, разработки оригинальных математических моделей и применения количественных методов исследования свойств таких моделей с помощью ПК.

Исследования модели будет состоять из:

-описания модели поведения потребителя в условиях совершенной конкуренции,

-построения математической модели,

-нахождения равновесия потребителя для случая двух частично взаимозаменяемых благ с нелинейной функцией полезности,

-проведения исследования на ЭВМ с применением экономико-математических методов свойств данной модели и их экономической интерпретации.

1. Экономическая постановка задачи и характеристика объекта

В теории потребления основной задачей математической является построение формализованной теории поведения потребителя. Основными составляющими этого процесса являются разработка математических моделей потребления и изучение на основе исследования свойств таких моделей закономерностей поведения потребителей в зависимости от экономической ситуации и институционального устройства экономики .

В основе модели потребителя лежит гипотеза о том, что потребители, осуществляя выбор благ при установленных ценах и имеющемся доходе, стремятся максимизировать уровень удовлетворения своих потребностей.

Рассмотрим основные понятия модели поведения потребителя.

Экономические блага - это средства для удовлетворения потребностей, доступные в orpaниченном количестве.

Как определить стоимость экономического блага? К.Маркс предлагал рассчитывать ее, исходя из трудовых затрат на производство этого товара. А по мнению неоклассиков (последователей классической теории экономики), стоимость благ зависит от того, насколько они редки (то есть от степени их ограниченности), то есть от интенсивности потребности в благе и от количества блага, способного эту потребность удовлетворить. При этом предполагается, что каждая потребность может быть удовлетворена несколькими видами благ, а каждое экономическое благо может быть использовано для удовлетворения нескольких потребностей.

Потребитель — гражданин, имеющий намерение заказать или приобрести либо заказывающий, приобретающий или использующий товары (работы, услуги) исключительно для личных, семейных, домашних и иных нужд, не связанных с осуществлением предпринимательской деятельности.

Потребности людей различаются по степени неотложности: на первом месте стоят потребности в еде, питье, одежде, безопасности, жилище (ради безопасности, как мы знаем, беженцы покидают свои жилища); затем потребности в общении, принадлежности к коллективу, наконец, потребности в интересной работе, в творчестве. Набор необходимых потребностей человека несколько различается в разные исторические эпохи и в разных странах (самый яркий пример — климатические различия: жители жарких стран испытывают потребность не в отоплении, а наоборот, — в охлаждении воздуха).

Из-за бюджетного ограничения потребителя, ему приходиться економить, выбирать благо по цене и качестве, при этом он комбинировает благи с максимальной совокупной полезности для себя. Этот выбор благ должен быть наилучшим с его точки зрения, то есть приносить ему наибольшую полезность, наибольшую степень удовлетворения.

Потребительский набор представляет собой комбинацию доступных потребителю товаров и услуг при его бюджетном ограничении.

В теории поведения потребителя можно выделить следующие аксиомы:

аксиома совершенной упорядоченности исходит из того, что любые два набора можно сравнить между собой;

потребитель ведет себя рационально, т.е. он последователен в своих предпочтениях и его предпочтения транзитивны;

аксиома рефлексивности предполагает, что предпочтения потребителя уже сформированы, т.е. он может оценить любой возможный набор товаров и услуг и делает свой выбор разумно;

аксиома ненасыщенности: согласно которой увеличение количества какого-то товара в наборе ведет к возрастанию полезности набора, так что потребитель всегда будет стремиться к получению все большего количества товаров.

2. Математическая постановка модели поведения потребителя

2.1 Математическая постановка задачи поведения потребителя

Всем компонентам исследуемого объекта, выписанных в предыдущем разделе поставим в соответствие подходящие математические конструкции.

Математическая модель произвольного блага в теории потребления выглядит следующим образом : - количество потребляемого блага, где h - индекс вида благ. , где l – число видов благ в наборе. Потребляемый набор благ – вектор , тогда

- множество доступных для потребителя наборов благ, обусловленное действием физических ограничений (). является подмножеством (), следовательно, все возможные наборы благ являются векторами l-мерного евклидова пространства Rl.

Сформулируем одну из наиболее часто употребляемых гипотез относительно множества физически возможных наборов благ.

Гипотеза 1. Множество X выпукло, замкнуто и ограничено снизу. Оно со-держит нулевой вектор. Если в нем содержится вектор x1 оно содержит в себе все векторы x2 такие, что x2h ≥ x1h для h = 1, 2, …, l.

- цена h-го блага, то - вектор цен. тогда, стоимость набора благ:

- доход потребителя (бюджет потребителя).

Помимо физических ограничений, выражаемых принадлежностью x множеству X, потребление потребителя подчинено экономическому (бюджетному) ограничению, которое задается неравенством

px ≤ R, (2.2)

где p и R заданы экзогенно.

То есть потребители могут выбирать только такие наборы благ, стоимость которых не превышает дохода. Бюджетное ограничение является обязательным экономическим ограничением в любой модели поведения потребителя.

- функция полезности. Она формализует и представляет систему предпочтений потребителя.

Рассмотрим гипотезы относительно функции полезности S (х)

Гипотеза 2. Функция S, определенная на X, является непрерывной и возрастающей функцией в том смысле, что если x1i> x2i для i = 1, 2, . .., l, то S (x1) > S (x2)

Т.е. если набор x1 более предпочтительный, чем x2, то S(x1)>S(x2).

Эта гипотеза исключает возможность состояния полного насыщения, при котором удовлетворение уже не может больше возрастать. В то же время она не исключает случай асимптотического приближения уровня удовлетворения потребителя с ростом количества потребленного блага к некоторому пределу.

Гипотеза 3. Функция S имеет производные второго порядка, а ее первые производные не могут быть все одновременно равны нулю.

Эта гипотеза введена для удобства проведения математических рассуждений. Это будет особенно наглядно при рассмотрении некоторых предельных равенств и при проведении рассуждений с помощью аналитического расчета.

Гипотеза 4. Функция S(x) строго квазивогнутая в том смысле, что если S(x2)≥S(x1) для двух наборов разных наборов благ x1 и x2, то S(x)>S(x1) для всех наборов х в открытом интервалы (x1, x2), т. е. для всех x, определяемых соотношениями

xi = бx1i+ (1-б)x2i, i = 1, 2, …, k,

где

Таким образом, в общем виде модель поведения потребителя описывается при помощи следующей оптимизационной задачи:

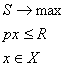(2.3)

Равновесием для потребителя называется вектор такой, который максимизирует функцию полезности S(x) при выполнении ограничений задачи (2.3).

Таким образом, моделью поведения потребителя является оптимизационная задача вида (2.3), а поведением (равновесным поведением) потребителя – оптимальное решение этой задачи.

2.2 Обоснование выбора модели поведения потребителя

Доход Потребителя = 6;

Потребитель потребляет два вида благ , где , 0;

- цены на первое и второе благо соответственно

P {}– вектор цен.

Тогда стоимость набора благ:

Потребитель располагает бюджетом R.

Бюджетное ограничение потребителя:

;

Зададим функцию полезности, представляющую систему предпочтений потребителя:

где - мультипликативная функция полезности. Была выбрана данная функция, поскольку она непрерывна, возрастающая, строго "квазивогнутая" и её первые производные не обращаются в ноль одновременно, что отвечает перечисленным выше гипотезам. Мультипликативная функция описывает полезность от потребления частично взаимозаменяемых благ.

3. Метод и алгоритм анализа модели

В экономической науке используются главным образом математические модели, описывающие изучаемые явления с помощью системы математических выражений. Каждая из них характеризует определенную взаимосвязь параметров исследуемого явления, отдельного его свойства и основные условия, например, между производством и потреблением, между потребностью в ресурсах и их наличием, между уровнем выхода продукции и факторами, его определяющими. Естественно, что чем сложнее изучаемая система или явление, тем более сложен процесс разработки экономико-математической модели и методики моделирования исследуемого объекта.

Один из наиболее общих и универсальных методов исследования реальных экономических процессов, протекающих в обстановке воздействия случайных возмущений и колебаний значений основных параметров и характеристик является экономико-математическое моделирование.

Применение метода количественных испытаний, а следовательно, и статистического моделирования неразрывно связано использованием вычислительной техники. Моделирование экономических процессов производится в несколько этапов:

- определение параметров процесса;

- моделирование процесса с помощью последовательности случайных чисел;

- определение искомых характеристик процесса и экономическая оценка результатов моделирования.

Таким образом, сущность моделирования заключается в численном воспроизведении случайных процессов по некоторым заранее известным параметрам и в определении неизвестных параметров в результате исследования модели.

В виде программного обеспечение выбираем средство Microsoft Excel, в котором присутствует надстройка «Поиск решения»

Что касается требований к конфигурации вычислительной техники, то для решения поставленной задачи можно воспользоваться персональным компьютером с конфигурацией, которая поддерживает операционную систему Windows и MS Office.

Используя пакет MS EXEL и надстройку «Поиск решений» задаем план эксперимента модели, при заданных ограничениях математической модели.

Выбираем диапазон ячеек А1:М1 и размещаем данные следующим образом (см. табл.1)

Табл. 1

p1*x1

p2*x2

b1+b2

p1*x1+p2*x2

Далее следует определить параметры модели:

Страницы: 1, 2, 3, 4

МЕНЮ

Курсовая работа: Построение модели поведения потребителя в условиях совершенной конкуренции

Курсовая работа: Построение модели поведения потребителя в условиях совершенной конкуренции

ИНТЕРЕСНОЕ