Курсовая работа: Статистическая обработка данных. Статистика денежного обращения

По формуле Стерджесса длина частичного интервала равна:

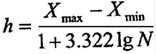= 0,548717225

Для удобства и простоты расчетов округляем полученный результат до сотых: h = 0,55

За начало первого интервала принимаем значение:

Хо= Хmin - h/2 = 14,13

Х1=Х0 + h = 14,67

Х2 = Х1+h = 15,22

Х3 = Х2 + h = 15,77

Х4=16,32

Х5=16,87

Х6=17,42

Х7=17,97

Х8 = 18,52

Вычисление границ заканчивается как только выполняется неравенство

Хn >X max: Х8 = 18,52 > Хmax = 18, 19

По результатам вычислений составляем таблицу. В первой строке таблицы помещаем частичные интервалы, на второй строке - середины интервалов, в третьей строке записано количество элементов выборки, попавших в каждый интервал частоты, в четвертой строке записаны относительные частоты и в пятой строке записаны значения плотности относительных частот или значения выборочной, экспериментальной функции плотности (таблица 1.4.2).

Таблица 1.4.2

Значение выборочной функции и плотности

Интервалы h	[14,33; 14,67)	[14,67; 15,22)	[15,22; 15,77)	[15,77; 16,32)	[16,32,16,87)	[16,87; 17,42)	[17,42; 17,97)	[17,97; 18,52)
	14,40	14,95	15,50	16,05	16,59	17,14	17,69	18,24
частота ni	2	12	10	14	10	8	3	1
	0,033333333	0,2	0,166666667	0,233333333	0,166666667	0,133333333	0,05	0,016666667
	0,060747744	0,364486462	0,303738718	0,425234206	0,303738718	0,242990975	0,091121615	0,030373872
	60,747744	364,486462	303,738718	425,234206	303,738718	242,990975	91,121615	30,373872

По результатам вычислений функции плотности, представленной в таблице 4.1 можно сделать вывод, что мода имеет один локальный максимум в окрестностях точки х=0.34 с частотой n=20.

Оценку медианы находим, используя вариационный ряд

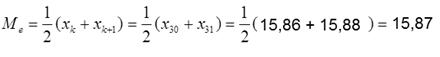
Т.к. N=2k, то k=N/2=30

Сравнение оценок  медианы = 15,87 и оценки математического ожидания 16,0515 показывает, что они отличаются на 1,14 %.

1.5 Параметрическая оценка функции плотности распределения

Исходя из гипотезы, что заданная выборка имеет нормальный закон распределения, найдём параметрическую оценку функции плотности, используя формулу для плотности распределения вероятности нормального закона

где  и  известны - они вычисляются по выборке.

=0,899484

=16,0515

Значения этой функции вычисляют для середин частичных интервалов вариационного ряда, т.е. при . На практике для упрощения вычислений функции , где i=1,2,…,k, пользуются таблицами значений функции плотности стандартной нормальной величины.

Для этого вычисляем значения 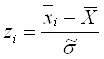 для i=1,2,…,k:

,

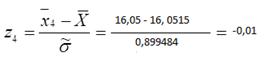
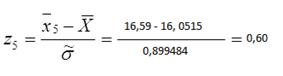
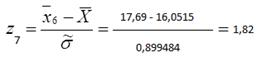Затем по таблице находим значение

:

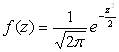0,0775

 0,1895

 0,3271

 0,3986

 0,3230

 0,1804

0,0694

0,0184

И после вычисляем функцию :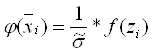

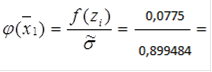0,0862

0,2107

 0,3637

0,4431

0,3591

0, 2006

0,0772

0,0205

Функция , вычисленная при заданных параметрах  и  в середине частичного интервала фактически является теоретической относительной частотой, отнесённой к середине частичного интервала

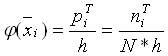
поэтому для определения теоретической частоты , распределённой по всей ширине интервала, эту функцию необходимо умножить на N*h.

, где h=0,55

0,55*0,0862= 0,0473

0,1156

0, 1995

0,2432

0, 1970

0,1101

p7T=0,0423

p8T=0,0112

 где N=60

0,0473*60= 2,8367

6,9361

11,9726

 14,5896

11,8225

6,6030

n7T=2,5402

n8T=0,6735

Результаты вычислений вероятностей и соответствующих частот приведены в таблице 5.1.

Таблица 1.5.1

[14,33; 14,67)	2	14,40	0,0333	0,0607	-1,84	0,0862	0,0473	2,8367
[14,67; 15,22)	12	14,95	0,2	0,3644	-1,23	0,2107	0,1156	6,9361
[15,22; 15,77)	10	15,50	0,1666	0,3037	-0,62	0,3637	0, 1995	11,9726
[15,77; 16,32)	14	16,05	0,2333	0,4252	-0,01	0,4431	0,2432	14,5896
[16,32,16,87)	10	16,59	0,1666	0,3037	0,60	0,3591	0, 1970	11,8225
[16,87; 17,42)	8	17,14	0,1333	0,2429	1,21	0, 2006	0,1101	6,6030
[17,42; 17,97)	3	17,69	0,05	0,0911	1,82	0,0772	0,0423	2,5402
[17,97; 18,52)	1	18,24	0,0166	0,0303	2,43	0,0205	0,0112	0,6735
	60		1				0,9662	57,9742

Страницы: 1, 2, 3, 4, 5, 6, 7