Курсовая работа: Статистическая обработка данных. Статистика денежного обращения

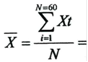16,0515

2. Среднее линейное отклонение - определяется как среднее арифметическое абсолютных значений вариант х-итое и среднего арифметического х-с-чертой

=0,7447

3. Дисперсия случайной величины X - мера разброса данной случайной величины, то есть её отклонения от математического ожидания

0,795586

4. Несмещенная оценка дисперсии

0,809071

5. Среднее квадратическое отклонение

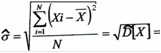0,86296

6. Несмещенная выборочная оценка для среднего квадратического отклонения

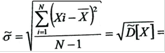0,899484

7. Коэффициент вариации

=5,603735

8. Коэффициент асимметрии случайной величины X

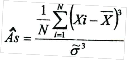=0,069231

Коэффициент асимметрии положителен, значит "длинная часть" кривой распределена справа от математического ожидания

9. Коэффициент эксцесса случайной величины X

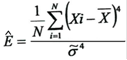3= - 0,68119

Для нормального распределения коэффициент эксцесса равен 0

Так как коэффициент отрицательный, то это значит, что сравниваемая кривая имеет более плоскую вершину, чем при нормальном распределении

10. Вариационный размах - показывает, насколько велико различие между наибольшей и наименьшей единицами совокупности

R = X max - X min=3,79

На основании полученных вычислений можно сделать следующие выводы:

1. Необходимое условие для того, чтобы выборка имела нормальный закон распределения, выполняется, т.к. для коэффициента вариации V выполняется неравенство:

V = 5,603735% < 33%

Отсюда следует, что все выборочные значения случайной величины X положительны, что мы и видим в исходных данных.

2. Для нормального распределения коэффициенты асимметрии и эксцесса должны быть равны нулю, т.е. Аs = Е = О

Выборочный коэффициент асимметрии служит для характеристики асимметрии распределения случайной величины. Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен 0.

По результатам вычисления асимметрия близка к нулю Аs = 0,069231.

В связи с этим необходимы дополнительные исследования для выяснения степени близости распределения выборки к нормальному распределению.

1.3 Результаты вычисления интервальных оценок для математического ожидания и дисперсии

Для вычисления интервальной оценки математического ожидания воспользуемся формулой:

Где a=M [X] - математическое ожидание,

N-1=V=59 - число степеней свободы,

 - величина, численно равная половине интервала, в который может попасть случайная величина , имеющая определённый закон распределения при заданной доверительной вероятности р и заданном числе степеней свободы V.

Подставляем в формулу вычисленные ранее значения , и N. В результате получим

16,0515 - t59,p (0,899484/√60) ‹a‹16,0515 + t59,p (0,899484/√60)

Задаёмся доверительной вероятностью ;

Для каждого значения  (i=1,2) находим по таблице значения и вычисляем два варианта интервальных оценок для математического ожидания.

1. При  

16,0515 - 2 (0,899484/√60) = 15,81925

16,0515 + 2 (0,899484/√60) = 16,28375

15,81925 < a < 16,28375

2.При  t59; 0,99= 2,66

16,0515 - 2,66 (0,899484/√60) = 15,74261

16,0515 + 2,66 (0,899484/√60) = 16,36039

15,74261 < a < 16,36039

Для интервальной оценки дисперсии существуют следующие неравенства:

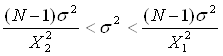
Подставляем в неравенство известные значения N и получим неравенство, в котором неизвестны  и .

(59*0,809071) /Х22<σ2< (59*0,809071) / Х12

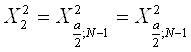
Задаваясь доверительной вероятностью  (или уровнем значимости а) вычисляем значения  и . Используем эти два значения и степень свободы V=N-1 по таблице находим  и

 и  - это границы интервала, в который попадает случайная величина Х, имеющая  распределение вероятности  и заданной степени свободы V.

Для =0,95

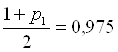
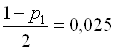  и V=59 находим по таблице:

Подставляя в неравенства  и  и произведя вычисления, получим интервальную оценку:

(59*0,809071) /83,2976<σ2< (59*0,809071) / 40,4817

0,573068<σ2<1,179179

Для

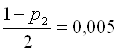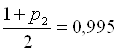;  и V=59 находим по таблице:

,

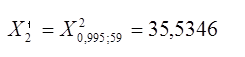Подставляя в неравенства  и  и произведя вычисления, получим интервальную оценку:

(59*0,809071) /91,9517<σ2< (59*0,809071) / 35,5346

0,519133<σ2<1,343343

Для интервальной оценки среднего квадратического отклонения имеем

При

σ = 0,899484

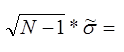
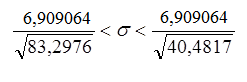6,909064

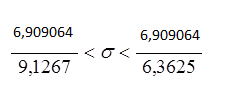
0,757017<σ<1,085904

При

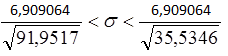
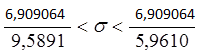
0,093802<σ< 0,368412

1.4 Результаты ранжирования выборочных данных вычисления моды и медианы

Используя исходные данные, записываем все заданные значения выборки в виде неубывающей последовательности значений случайной величины Х.

Таблица 1.4.1

Ранжированный ряд

1	14,4	11	15,15	21	15,61	31	15,88	41	16,4	51	17,02
2	14,44	12	15,15	22	15,64	32	15,93	42	16,4	52	17,12
3	14,85	13	15,22	23	15,68	33	15,96	43	16,52	53	17,26
4	15,01	14	15,22	24	15,7	34	16,05	44	16,6	54	17,36
5	15,02	15	15,26	25	15,78	35	16,26	45	16,62	55	17,38
6	15,03	16	15,28	26	15,8	36	16,29	46	16,67	56	17,39
7	15,04	17	15,31	27	15,81	37	16,3	47	16,75	57	17,7
8	15,07	18	15,38	28	15,81	38	16,31	48	16,84	58	17,78
9	15,1	19	15,41	29	15,85	39	16,38	49	16,91	59	17,94
10	15,12	20	15,59	30	15,86	40	16,38	50	16,91	60	18, 19

Интервал [14,40; 18, 19], содержащий все элементы выборки, разбиваем на частичные интервалы, используя при этом формулу Стерджесса для определения оптимальной длины и границ этих частичных интервалов.

Страницы: 1, 2, 3, 4, 5, 6, 7