Контрольная работа: Определение статистических данных производства продукции

Задача 5

Реализация товаров на колхозном рынке характеризуется данными представленными в табл.5.

Таблица 5.

Наименование товара	Базисный период		Отчетный период
	Количество, тыс. кг.	Цена 1 кг., грн	Количество, тыс. грн.	Цена 1 кг., грн
Картофель	15,0	0,3	20	0,5
Мясо	3,0	3,5	4	5

Определите:

1) общий индекс физического объема продукции;

2) общий индекс цен и абсолютный размер экономии (перерасхода) от изменения цен;

3) на основании исчисленных индексов определить индекс товарооборота.

Решение.

Индекс представляет собой относительную величину, получаемую в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или с планом.

Индивидуальными называются индексы, характеризующие изменения только одного элемента совокупности.

Общий индекс отражает изменение по всей совокупности элементов сложного явления.

Стоимость - это качественный показатель.

Физический объем продукции - количественный показатель.

Общий индекс физического объема продукции вычисляется по формуле:

,

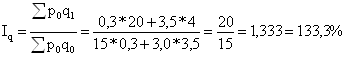где p0 и р1 - цена единицы товара соответственно в базисном и отчетном периодах;

q0 и q1 - количество (физический объем) товара соответственно в базисном и отчетном периодах.

Количество проданных товаров увеличилось на 33,3%.

Или в деньгах: 20 - 15 = 5,0 тыс. грн.

Общий индекс стоимости вычисляется по формуле:

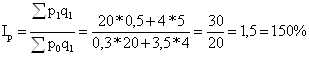
Следовательно, цены на данные товары в среднем увеличились на 50%.

Сумма сэкономленных или перерасходованных денег:

сумма возросла на 50%, следовательно, население в отчетном периоде на покупку данных товаров дополнительно израсходует: 30 - 20 = 10 тыс. грн.

Общий индекс товарооборота вычисляется по формуле:

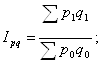
Товарооборот в среднем возрос на 100%.

Взаимосвязь индексов:

1,333 * 1,5 = 2,0

Задача 6

Имеются данные о выпуске одноименной продукции и её себестоимости по двум заводам

Завод	Производство продукции, тыс. шт.		Себестоимость 1 шт., грн.
	I квартал	II квартал	I квартал	II квартал
I	100	180	100	96
II	60	90	90	80

Вычислите индексы:

1) себестоимости переменного состава;

2) себестоимости постоянного состава;

3) структурных сдвигов. Поясните полученные результаты.

Решение.

Индекс себестоимости переменного состава вычисляется по формуле:

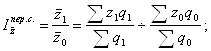
где z0 и z1 - себестоимость единицы продукции соответственно базисного и отчетного периодов;

q0 и q1 - количество (физический объем) продукции соответственно в базисном и отчетном периодах.

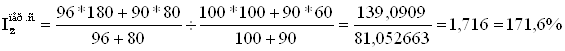
Индекс показывает, что средняя себестоимость по двум заводам повысилась на 71,6%, это повышение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры продукции (увеличением объема выпуска).

Выявим влияние каждого из этих факторов.

Индекс себестоимости постоянного состава вычисляется по формуле:

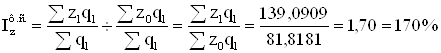
То есть себестоимость продукции по двум заводам в среднем возросла на 70%.

Индекс себестоимости структурных сдвигов вычисляется по формуле:

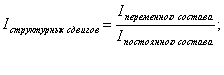
Или

Взаимосвязь индексов:

170*100,9=171,6

Вывод:

Индекс себестоимости переменного состава зависит от изменения уровня себестоимости и от изменения объема производства, т.е. средний прирост себестоимости составил 71,6%.

Индекс себестоимости постоянного состава показывает изменение себестоимости при фиксированном объеме производства, т.е. в среднем по заводам себестоимость повысилась на 71%. Индекс себестоимости переменного состава выше, чем индекс себестоимости постоянного состава, это свидетельствует о том, что произошли благоприятные структурные сдвиги. Индекс структурных сдвигов равен 1,009%, т.е. за счет изменения объемов производства по заводам средняя себестоимость повысилась на 0,9%.

Задача 7

Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак Y) и оснащенностью заводов основными производственными фондами (факторный признак X) по данным задачи 1 вычислить коэффициент детерминации и эмпирическое корреляционное отношение.

Решение.

Показателем тесноты связи между факторами, является линейный коэффициент корреляции.

Линейный коэффициент корреляции вычислим по формуле:

.

Линейное уравнение регрессии имеет вид: y=bx-а.

Коэффициент детерминации показывает насколько вариация признака зависит от фактора, положенного в основу группировки и вычисляется по формуле:

где d2 - внутригрупповая дисперсия;

s2 - общая дисперсия.

Общая дисперсия характеризует вариацию признака, который зависит от всех условий в данной совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием фактора, положенного в основу группировки и рассчитывается по формуле:

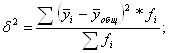
где среднее значение по отдельным группам;

fi - частота каждой группы.

Средняя из внутригрупповых дисперсия:

где  - дисперсия каждой группы.

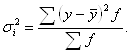
Эмпирическое корреляционное отношение рассчитывается по формуле:

Все расчетные данные приведены в таблице 7.

Таблица 7

№ завода	Среднегодовая стоимость ОФ, млн. грн. (X)	Валовая продукция в сопоставимых ценах, грн. (Y)	X^2	Y^2	XY
1	1,6	1,5	2,56	2,25	2,55
2	3,9	4,2	15,21	17,64	17,16
3	3,3	4,5	10,89	20,25	15,75
4	4,9	4,4	24,01	19,36	22,05
5	3,0	2,0	9	4	6,4
6	5,1	4,2	26,01	17,64	22,44
7	3,1	4,0	9,61	16	13,2
8	0,5	0,4	0,25	0,16	0,1
9	3,1	3,6	9,61	12,96	11,52
10	5,6	7,9	31,36	62,41	43,68
11	3,5	3,0	12,25	9	10,8
12	0,9	0,6	0,81	0,36	0,63
13	1,0	1,1	1	1,21	1,32
14	7,0	7,5	49	56,25	53,9
15	4,5	5,6	20,25	31,36	25,76
16	8,1	7,6	65,61	57,76	63,18
17	6,3	6,0	39,69	36	38,4
18	5,5	8,4	30,25	70,56	46,75
19	6,6	6,5	43,56	42,25	43,55
20	1,0	0,9	1	0,81	0,8
21	4,7	4,5	22,09	20,25	21,6
22	2,7	2,3	7,29	5,29	6,75
23	2,9	3,2	8,41	10,24	8,96
24	6,8	6,9	46,24	47,61	46,24
Итого	95,6	100,8	485,96	561,62	523,49
Среднее	3,824	4,032	19,4384	22,4648	21,81

Подставив вычисленные значения в формулу, получим:

Коэффициент детерминации h2 = 0,87.

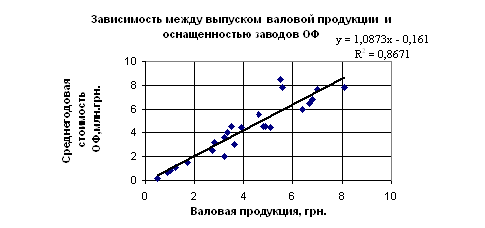
Эмпирическое корреляционное отношение имеет вид: у = 1,0873х - 0,161.

Линейный коэффициент корреляции r = 0,93.

a=0,161b=1,0873

Так как значение коэффициента корреляции близко к единице, то между выпуском валовой продукции и оснащенностью заводов основными производственными фондами есть тесная зависимость.

b - коэффициент регрессии, т.к b > 0, то связь прямая.

Список использованной литературы

1.  1. Адамов В.Е. Факторный индексный анализ. - М.: Статистика, 1997.

2.  2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. - М.: Финансы и статистика, 2004.

3.  3. Ефимова М.Р., Рябцев В.Ф. Общая теория статистики: Учебник. М.: Финансы и статистика, 1999.