Курсовая работа: Структурный, кинематический и силовой анализ механизма. Синтез зубчатой передачи

Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими названию точек.

Считая известными ускорения шарнирных точек
(аО = аО = 0), помещаем их на плане ускорений в полюсе рa. Звено О1А вращается равномерно, поэтому точка А имеет только нормальное ускорение , которое направлено по звену О1А к центру вращения О1 (см. рис. 2.3, в). Определяем его по формуле, м/с2 :

; . (2.22)

Принимаем (произвольно) длину отрезка , изображающего вектор ускорения  точки А, равной 180 мм. Тогда масштаб плана ускорений, м/с2×мм-1,

; . (2.23)

Из полюса плана ра откладываем  параллельно звену О1А в направлении от А к О1.

Рассматривая движения точки В со звеном АВ, составляем векторное уравнение:

, (2.24)

в котором ускорение точки А известно по значению и направлению. Определяем нормальное ускорение точки В относительно А, м/с2 ,

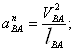
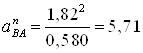 ; (2.25)

 .

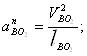
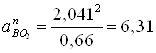От точки а плана ускорений параллельно звену АВ в направлении от точки В к точке А откладываем вектор , изображающий ускорение аВАn , величина которого:

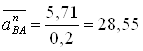;  мм (2.26)

Через точку n1 проводим перпендикулярно звену АВ линию действия тангенциального ускорения аВАф. Из точки О2 плана ускорений параллельно звену О2В в направлении от В к О2 откладываем вектор , изображающий ускорение аВО2n, величина которого:

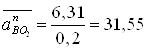  мм (2.27)

Через точку n2 проводим перпендикулярно звену О2В линию действия тангенциального ускорения аВО2ф . На их пересечении получится точка В – кон

ец вектора  изображающего ускорение аВ точки В механизма, м/с2:

 . (2.28)

Определяем тангенциальные ускорения и относительные во вращении вокруг точек А и О2, м/с2:

; ;

; ;

  (2,29)

   

Положение точки С на плане ускорений находим по свойству подобия (из пропорции):

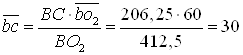; мм. (2.30)

Соединив ее с полюсом, определяем ускорение точки С, м/с2:

 . (2.31)

Величины ускорений центров тяжести звеньев S1, S2, S3, м/с2:

 ;

 ; (2.32)

 

Определения ускорения точки D рассматриваем движения точки D со звеньями СD. Составляем векторные уравнения:

; (2.33)

Определяем нормальное ускорение точки D (ускорение точки С известно по значению и направлению), м/с2:

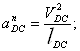
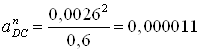 . (2.34)

На плане ускорений  можно выразить:

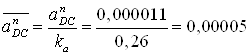мм (2.35)

Отложим его параллельно звену CD на плане из точки С в направлении от D к С, а затем перпендикулярно звену CD провести линию действия тангенциального ускорения до пересечения с линией хода ползуна (это будет точка D).

Определим величины ускорений точек D, , , , , м/с2:

 ;

  (2.36)

 ;

 ;

 ;

Определяем угловые ускорения звеньев.

Угловое ускорение e1 ведущего звена О1А, совершающего равномерное движение, равно нулю.

Угловое ускорение звена 2, с-2 ,

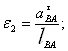
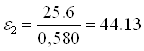 . (2.35)

Для определения направления углового ускорения e2 звена 2 надо мысленно перенести вектор  тангенциального ускорения  в точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки.

По аналогии определяем значения и направления угловых ускорений звеньев 4 и 5, с-2:

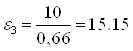;  (по часовой стрелки);

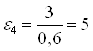;  (по часовой стрелки). (2.36)

3. СИЛОВОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМОВ

В задачу силового исследования входит определение:

1) сил, действующих на звенья механизма;

2) реакций в кинематических парах;

3) уравновешивающей силы (момента).

Силовой анализ основан на принципе Даламбера. Сущность его заключается в том, что каждое звено может рассматриваться в условном статическом равновесии, если к нему помимо всех действующих внешних сил приложить инерционную нагрузку в виде силы инерции и момента пары сил инерции. При этом условии для каждого звена справедливы равенства:

 , (3.1)

поэтому неизвестные силы (реакции в кинематических парах) могут определяться методом статики.

Для проведения силового анализа кинематическая цепь должна быть статически определимой, т. е. число неизвестных параметров реакций должно быть равно количеству уравнений статики, которые можно составить для их определения.

Начинать силовой анализ необходимо с наиболее удаленной от ведущего звена структурной группы.

3.1 Определение реакций в кинематических парах структурных групп

Чтобы определить величины и направления сил инерции, надо знать ускорения и массы звеньев. Ускорения известны из плана ускорений механизма. Определяем вес каждого звена, Н:

;

;

; (3.2)

;

;

где  - длина звеньев, мм.

Определяем массу каждого звена, кг:

 

; ;

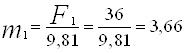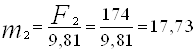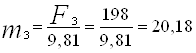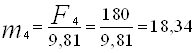; ; (3,3)

.

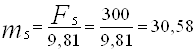Определяем силы инерции звеньев, Н:

;

;

; (3.4)

;

.

Определяем момент пары сил инерции для звеньев CD, О2B и AВ, совершающих сложное движение:

звено АВ-

 (3.5)

 

звено О2B-

;

 ; (3.6)

звено СD-

 (3.5)

Силовой расчет механизма начинаем с наиболее удаленной от ведущего звена группы Ассура 4 – 5 (CD), состоящей из звеньев 4 и 5, двух вращательных кинематических пар – С и D, и одной поступательной (при движении ползуна по направляющей).

Группу CD вычерчиваем отдельно в масштабе схемы механизма и в том же положении. Прикладываем к ней вместо связей две реакции:

F65 – в поступательной паре, другую F34 в шарнире С, неизменные по величине и направлению. Реакцию F34 представляем в виде двух составляющих: тангенциальной , направленной перпендикулярно к оси звена CD, и нормальной  - вдоль звена CD.

Кроме этого прикладываем силы веса F4 и F5 в центрах тяжести и силы инерции:  - против ускорения тяжести S4 ;  - против ускорения ползуна . Момент инерции заменяем парой сил: , приложенной в точке С против направления углового ускорения звена 4 (e4), и  - в точке D.

Для определения реакций в кинематических парах составляем векторное уравнение равновесия сил, действующих на группу 4 – 5 по порядку звеньев:

. (3.7)

Силы  и  в уравнение не вписаны, так как они решается построением плана сил, и эти силы взаимно уравновешивают друг друга, но для определения  эти силы надо знать, Н:

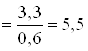; ; (3.8)

Определяем , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:

; (3.9)

 

 Н.

Поскольку составляющую  получилась со знаком плюс, то это значит, что ее действительное направление совпадает с выбранным.

Исходя из значений сил, входящих в уравнение равновесия, Н:

; ; ; ;

; ; (3.10)

задаемся масштабом плана сил , Н/мм.

Максимальной силой является сила полезного сопротивления, которую в примере изобразим вектором длиной 250 мм. Получаем масштаб плана сил, Н × мм-1:

. (3.11)

Вычисляем длины векторов, мм, изображающих эти силы, поделив их численные значения на масштаб:

 ;                ;

 ;                   (3.12)

 (задались);           

От произвольной точки – полюса плана сил – параллельно силе  откладываем вектор  изображающий эту силу; от конца вектора  параллельно силе  откладываем в том же направлении вектор  и далее векторы всех сил. Через точку а параллельно звену СD проводим линию действия , а через конец вектора  перпендикулярно к направляющей ползуна – линию действия силы . Точка пересечения этих линий действия определяет силы , ,  Н:

 ; (3.13)

 ;

 

Далее следует отсоединить группу Ассура АВСО2, состоящую из звеньев 2 и 3, вычертить ее в масштабе. В соответствующих точках приложить действующие силы: . Реакцию в шарнире А и О2 представить в виде двух составляющих – , , , . Реакцию со стороны звена 4 на звено 3 , полученную из плана сил группы Ассура CD,  приложить в обратном направлении в точке С звена 2 .

Составляем векторное уравнение равновесия сил, действующих на группу Ассура 2 – 3 , по порядку звеньев:

. (3.17)

Силы ,, и  в уравнение не вписываем, так как это уравнение решается построением плана сил, и они взаимно уравновешивают друг друга. Но для определения  и эти силы надо знать, определяем их, Н:

  (3.1)

;

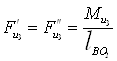Из уравнения моментов относительно точки В для звена 2 определяем составляющую , Н:

 (3.19)

отсюда,

; (3.20)

Размеры плеч  снимаем с чертежа в миллиметрах. Поскольку знак составляющей  изменился, то ее действительное направление не соответствует выбранному.

Определяем тангенциальную составляющую  из уравнения моментов относительно точки В для звена 3:

;

                                 (3.21)

Плечи , ,  снимаем с чертежа в миллиметрах. Поскольку составляющая  получилась со знаком минус, то это значит, что её действительное направление не совпадает с выбранным.

Выписав значения всех сил, Н, действующих на группу Ассура, по максимальной из них задаемся масштабом. Максимальную силу F43 изобразим вектором, длина которого 308 мм (произвольно), тогда:

 Н/мм.               (3.22)

Вычисляем длины векторов, изображающих эти силы, мм:

 ;   ;

Страницы: 1, 2, 3