Курсовая работа: Проектирование зубчатого и кулачкового механизмов

1.2 Проверка качества зубьев и зацепления

Проверка на не заострение:

Sa≥0,4∙m=0,4∙6=2,4 мм;

Sa1=3,017мм;

Sa2=4,338мм.

Проверка на отсутствие подрезания:

0,5∙z1∙sin2α ≥ h*a – x1;

0,5∙14∙0,1833 ≥ 1 – 0,519;

1,2831≥ 0,481.

0,5∙z2∙sin2α ≥ h*a – x2;

0,5∙30∙0,1833 ≥ 1 – 0,418;

2,7495≥ 0,582.

Для обеспечения плавности зацепления коэффициент перекрытия для силовых передач требуется принимать ε ≥ 1,15. За нашими подсчетами имеем

ε = 1,265

1.3 Расчет контрольных размеров

Размер постоянной хорды:

Sc=S∙cos2α;

Sc1=S1∙cos2α = 11,766∙0,883= 10,389мм;

Sc2=S2∙cos2α = 11,347∙0,883= 10,019мм.

Расстояние от окружности вершин до постоянной хорды:

Длина общей нормали:

W=Pb∙n∙Sb,

где n – количество шагов, охватываемых скобой (количество впадин).

n1=1, n2=3

W1=Pb1∙n+Sb1= 17,713∙1+12,233= 29,946 мм;

W2=Pb2∙n+Sb2=17,713∙3+13,183= 66,322мм.

1.4 Подбор чисел зубьев планетарного механизма

Подбор чисел зубьев колес z1, z2, z3, z4 и z5 планетарного механизма производится на ПК в программе ТММ.ЕХЕ.

Алгоритм подбора чисел зубьев колес z3, z4, z5 при числе сателлитов k=3 следующий.

Используя метод Виллиса, выражаем  через числа зубьев колес:

, откуда

Полученное число  меняем рядом простых дробей со знаменателем 16, 17, 18, … . Числитель каждой дроби получаем, перемноживши принятий знаменатель на  и откинув дробную часть … .

Рассматриваем дробь с наименьшим знаменателем. Приняли  равным знаменателю, а  равным числителю, определяем  с условия соосности.

откуда .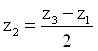

Если  получаем не целым, то числитель увеличиваем на 1 и опять определяем .

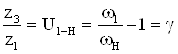
Проверяем передаточное отношение, задавшись допустимой его относительной погрешностью D.

Для этого считаем  и сравнивая его с заданным

: .

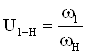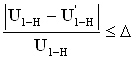Если неравность выполняется, то проверяем условия составления:

, ,

т.е. ,

где k – число сателлитов,

Е – любое целое число.

Для каждого вариант числа зубьев проверяем возможность установки на водило два, три или четыре сателлита.

После знаменатель дроби увеличиваем на 1 (переходим до исследования следующей дроби) и весь расчет повторяется. В такой способ можно перебрать множество дробей и получить набор вариантов  и соответствующим им значений «k», которые записываются в форме таблицы 1.

Таблица 1.2 - Значения

№
1	20	35	90	2	5,5
2	21	37	95	2,4	5,524
3	22	38	98	2,3,4	5,455
4	23	40	103	2,3	5,478
5	24	42	108	2,3,4	5,5
6	25	43	111	2,4	5,44

Таблица 1.3 - Выбор варианта набора чисел

№	Z1	Z2	Z3	Z4	K	Uф
3	22	38	98	0	2,3,4	5,455

Таблица 1.4 -Угловая скорость зубчатого колеса и водила рад/с

ω 1	ω 2	ω 3	ω 4	ω Н
113,098	-32,739	0	0	20,735

В связи с тем, что с ростом знаменателя растет числитель растут габариты механизма, при проектировании механизма целесообразным считаем диапазон знаменателя от 17 до 27.

С полученной таблицы выбираем оптимальный вариант из взгляда наименьших габаритов механизма с заданным числом сателлитов «k» и за условия отсутствия подрезания зубьев всех зубчатых колес.

Избраний вариант с k=3 и проверяется на выполнения условия соседства.

1.5 Кинематический анализ планетарного механизма

Определим радиусы начальных окружностей:

r1 = d1/2 = m·Z1/2= 6·14/2=84/2 = 42 мм

r2 =d2/2 = m·Z2/2= 6·30/2=180/2 = 90 мм

r3 = d3/2 = m·Z3/2= 6·22/2 =132/2 = 66 мм

r4 = d4/2 = m·Z4/2= 6·38/2=228/2 = 114 мм

r5 = d5/2 = m·Z5/2= 6·98/2 =588/2 = 294 мм.

Выбираем масштабный коэффициент: . С учетом масштабного коэффициента построим кинематическую схему редуктора. На кинематической схеме условно изображаем один сателлит.

Вычислим скорость точки А, принадлежащей окружности колеса 1:

,

Где .

Va = ω1∙151∙

Выбираю .

Скорость точки А является касательной к начальной окружности колеса 1  – вектор изображающий скорость точки А. Отрезок Аа - линия распределения скоростей точек колеса 1. Из точки В провожу горизонтальную линию. Из точки а через точку  провожу отрезок до пересечения с горизонтальной линией, проходящей через точку B. Полученный отрезок аb– линия распределения скоростей точек колес 2 и 3.

Строю диаграмму угловых скоростей:

.

Переношу на диаграмму угловых скоростей точку Р и распределения линейных скоростей параллельно самим себе.

Получаем угловые скорости колес графическим методом:

;

 

 

 

Проверим значения угловых скоростей аналитическим методом – методом Виллиса.

Механизм состоит из последовательно соединенных двух механизмов – простого и планетарного.

.

По методу Виллиса всем звеньям планетарного механизма дополнительно сообщаем скорость равную . Получаем обращенный механизм.

Передаточное отношение в обращенном механизме:

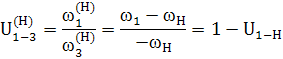
С другой стороны

Тогда

Таким образом, получаем:

;

 ;

Чтобы найти ω4, определим передаточное отношение :

с другой стороны

Таким образом, получаем

Сравнение угловых скоростей, полученных аналитически и графически, представлено в таблице 3.6.

Таблица 1.5 – Сравнение данных аналитического и графического методов

Метод определения	ω1, рад/с	ω2,3, рад/с	ω4, рад/с	ωН, рад/с
Аналитический
Графический
Расхождение, %	0	0, 02	0,01	0,01

Страницы: 1, 2, 3