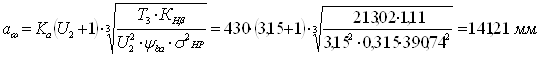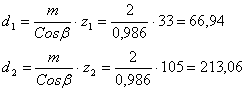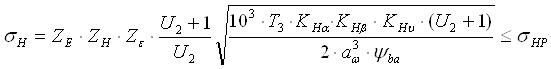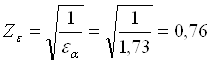| |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Курсовая работа: Расчет редуктора
Коэффициент долговечности
![]() находится
по формуле [ф. 3.14]:
находится
по формуле [ф. 3.14]:
 но не менее 1,
но не менее 1,
где ![]() – показатель степени [с.
14];
– показатель степени [с.
14];
![]() – базовое число циклов перемены
напряжений, NFlim = 4×106 циклов;
– базовое число циклов перемены
напряжений, NFlim = 4×106 циклов;
![]() – суммарное число циклов перемены
напряжений, уже определены:
– суммарное число циклов перемены
напряжений, уже определены:
![]() циклов,
циклов,
![]() циклов.
циклов.
Так как ![]() и
и ![]() , то
, то ![]() .
.
Предел выносливости при
отнулевом цикле изгиба ![]() , выбирается в зависимости от
способа термической или химико-термической обработки [приложение 2]:
, выбирается в зависимости от
способа термической или химико-термической обработки [приложение 2]:
для
шестерни с объемной
закалкой из стали марки 40ХН ![]() = 580 МПа, для колеса с улучшением стали марки
40ХН
= 580 МПа, для колеса с улучшением стали марки
40ХН ![]() =1,75*300;
=1,75*300; ![]() = 525 МПа.
= 525 МПа.
Коэффициент, учитывающий
влияние двустороннего приложения нагрузки ![]() , так как одностороннее приложение
нагрузки [c. 34].
, так как одностороннее приложение
нагрузки [c. 34].
![]()
Тогда:
![]()
![]()
3.2 Определение расчетного изгибного напряжения
Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса.
Выносливость зубьев, необходимая для предотвращения усталостного излома зубьев, устанавливают сопоставлением расчетного местного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения [ф. 5.1]:
![]() .
.
Расчетное местное напряжение при изгибе определяют по формуле, МПа:
 ,
,
где Т – крутящий момент, Н*м;
m – нормальный модуль, мм;
z – число зубьев;
![]() – коэффициент ширины зуба по диаметру (опреден ранее);
– коэффициент ширины зуба по диаметру (опреден ранее);
![]() – коэффициент, учитывающий форму
зуба и концентрацию напряжений;
– коэффициент, учитывающий форму
зуба и концентрацию напряжений;
![]() – коэффициент, учитывающий
влияние наклон зуба;
– коэффициент, учитывающий
влияние наклон зуба;
![]() – коэффициент, учитывающий
перекрытие зубьев;
– коэффициент, учитывающий
перекрытие зубьев;
![]() – коэффициент
нагрузки.
– коэффициент
нагрузки.
Коэффициент
![]() , учитывающий форму зуба и
концентрацию напряжений, определяется по формуле [ф. 3.17]:
, учитывающий форму зуба и
концентрацию напряжений, определяется по формуле [ф. 3.17]:
![]() ,
,
где
x3 = x4 = 0 – коэффициенты смещения; ![]() ,
, ![]() – так
как шестерни прямозубые. Тогда:
– так
как шестерни прямозубые. Тогда:
![]() ;
;
![]() .
.
Так как
![]() >
> ![]() ,
,
то дальнейший расчет будем проводить для колеса.
Коэффициент
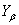 ,
учитывающий влияние угла наклона зубьев, для прямозубых колес равен 1.
,
учитывающий влияние угла наклона зубьев, для прямозубых колес равен 1.
Коэффициент ![]() , учитывающий перекрытие зубьев, берется равным 1.
, учитывающий перекрытие зубьев, берется равным 1.
Коэффициент нагрузки ![]() принимают по формуле [ф. 5.6]:
принимают по формуле [ф. 5.6]:
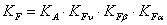 ,
,
где
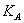 –
коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в
циклограмме нагружения);
–
коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в
циклограмме нагружения);
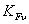 –
коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до
зоны резонанса;
–
коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до
зоны резонанса;
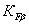 – коэффициент,
учитывающий неравномерность распределения нагрузки по длине контактных линий;
– коэффициент,
учитывающий неравномерность распределения нагрузки по длине контактных линий;
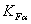 – коэффициент,
учитывающий распределение нагрузки между зубьями.
– коэффициент,
учитывающий распределение нагрузки между зубьями.
Коэффициент, учитывающий внешнюю динамическую нагрузку [т. 4.2]:
![]() = 1.
= 1.
Динамический коэффициент ![]() определен по таблице 5.1.
определен по таблице 5.1.
Коэффициент ![]() , учитывающий
неравномерность распределения нагрузки по длине контактных линий,
определяется по графику [р. 3.5], в зависимости от коэффициента
, учитывающий
неравномерность распределения нагрузки по длине контактных линий,
определяется по графику [р. 3.5], в зависимости от коэффициента ![]() :
:
![]() = 1,15.
= 1,15.
Коэффициент ![]() , учитывающий неравномерность распределения нагрузки
между зубьями, берется равным 1.
, учитывающий неравномерность распределения нагрузки
между зубьями, берется равным 1.
Таким образом:
![]() .
.
Тогда:
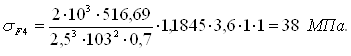
Сопоставим расчетные и допускаемые напряжения на изгиб:
![]() .
.
Следовательно, выносливость зубьев при изгибе гарантируется с вероятностью неразрушения более 99 %.
4. Расчет на контактную прочность при действии максимальной нагрузки
При действии максимальной
нагрузки ![]() наибольшее
за заданный срок службы контактное напряжение
наибольшее
за заданный срок службы контактное напряжение ![]() не должно превышать допускаемого
не должно превышать допускаемого ![]() [ф. 4.14] :
[ф. 4.14] :
![]()
Напряжение ![]() [ф. 4.15] :
[ф. 4.15] :
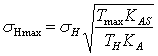 ,
,
где ![]() – коэффициент внешней
динамической нагрузки при расчетах на прочность от максимальной нагрузки (см.
приложение 4).
– коэффициент внешней
динамической нагрузки при расчетах на прочность от максимальной нагрузки (см.
приложение 4). ![]() =1.
=1.
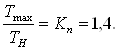
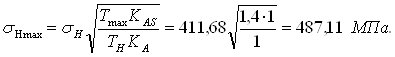
Допускаемое контактное
напряжение при максимальной нагрузке, не вызывающее остаточных деформаций или
хрупкого разрушения поверхностного слоя ![]() , зависит от способа химико-термической обработки
зубчатого колеса и от характера изменения твердости по глубине зуба. Для
зубчатых колес, подвергнутых улучшению или закалке принимают [ф. 4.16]:
, зависит от способа химико-термической обработки
зубчатого колеса и от характера изменения твердости по глубине зуба. Для
зубчатых колес, подвергнутых улучшению или закалке принимают [ф. 4.16]:
![]() ;
;
где ![]() – предел текучести,
Мпа.
– предел текучести,
Мпа.
Для стали 40ХН с закалкой
![]() =1400 МПа;
=1400 МПа;
Для стали 40ХН с
улучшением ![]() =600 МПа.
=600 МПа.
487,11 < 1680, зн. условие выполнено.
5. Расчет на прочность при изгибе максимальной нагрузкой
Прочность зубьев, необходимая для предотвращения остаточных деформаций, хрупкого излома или образования первичных трещин в поверхностном слое, определяют сопоставлением расчетного (максимального местного) и допускаемого напряжений изгиба в опасном сечении при действии максимальной нагрузки [ф. 5.16] :
![]() .
.
Расчетное местное
напряжение ![]() МПа,
определяют по формуле[ф. 5.17] :
МПа,
определяют по формуле[ф. 5.17] :
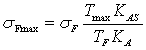 .
.
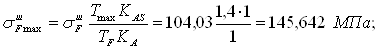
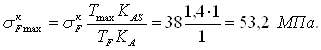
![]()
![]()
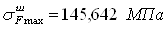 <
< 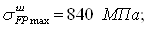
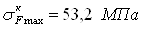 <
<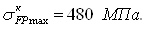
Зн. условия выполнены.
Расчет быстроходной передачи
Исходные данные:
U2 = 3,15 – передаточное число;
n2 = 727,5 об/мин – частота вращения шестерни;
n3 = 230,95 об/мин – частота вращения зубчатого колеса;
T2 = 69,7 Нм – вращающий момент на шестерне;
T3 = 213,02 Нм – вращающий момент на зубчатом колесе;
Pвых = 5 кВТ;
Коэффициент перегрузки при пуске двигателя Кпер = 1,4.
Материал шестерни – сталь 40ХН;
Материал колеса – сталь 40ХН;
Способ термической обработки:
шестерни – улучшение (Нш = 300 HВ);
колеса – улучшение (Нк = 300 HВ);
Срок службы – 19000 ч.
1. Проектировочный расчет
Выбираем коэффициент
ширины зуба ![]() с
учетом того, что имеем несимметричное расположение колес относительно опор:
с
учетом того, что имеем несимметричное расположение колес относительно опор: ![]() = 0,315 [с. 7].
= 0,315 [с. 7].
Тогда коэффициент ширины
зуба по диаметру ![]() определяем по формуле [ф. 3.1]:
определяем по формуле [ф. 3.1]: ![]() .
.
Проектный расчет заключается в определении межосевого расстояния проектируемой передачи [ф. 3.2]:
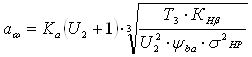 ,
,
где «+» для внешнего зацепления, «–» для внутреннего зацепления;
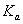 –
вспомогательный коэффициент;
–
вспомогательный коэффициент;
T3 – вращающий момент на валу колеса (на 3-м валу), Нм;
U2 – передаточное отношение;
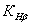 – коэффициент,
учитывающий неравномерность распределения нагрузки по длине контактных линий;
– коэффициент,
учитывающий неравномерность распределения нагрузки по длине контактных линий;
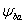 – коэффициент
ширины зуба;
– коэффициент
ширины зуба;
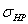 – допускаемое
контактное напряжение, МПа.
– допускаемое
контактное напряжение, МПа.
Для косозубой передачи
вспомогательный коэффициент ![]() = 430 [т. 3.1].
= 430 [т. 3.1].
![]() = 1,11 – данный коэффициент
принимают в зависимости от параметра
= 1,11 – данный коэффициент
принимают в зависимости от параметра ![]() , схемы передачи и твердости
активных поверхностей зубьев [р. 3.1].
, схемы передачи и твердости
активных поверхностей зубьев [р. 3.1].
Допускаемые
контактные 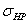 напряжения
определяют раздельно для шестерни и колеса по формуле [ф. 3.3]:
напряжения
определяют раздельно для шестерни и колеса по формуле [ф. 3.3]:
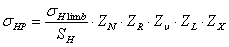 ,
,
где
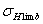 – предел
контактной выносливости, соответствующий базовому числу циклов напряжений, МПа;
– предел
контактной выносливости, соответствующий базовому числу циклов напряжений, МПа;
SH – коэффициент запаса прочности;
ZN – коэффициент долговечности;
ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;
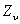 – коэффициент,
учитывающий окружную скорость;
– коэффициент,
учитывающий окружную скорость;
ZL – коэффициент, учитывающий влияние вязкости масла;
ZX – коэффициент, учитывающий размер зубчатого колеса.
![]() = 0,9;
= 0,9;
Тогда:
![]() .
.
Коэффициенты запаса
прочности: для шестерни и колеса из материала однородной структуры принимаем ![]() =1,2 и
=1,2 и ![]() = 1,2 [с. 9].
= 1,2 [с. 9].
Предел контактной
выносливости ![]() , МПа [т. 3.2]:
, МПа [т. 3.2]:
для шестерни ![]() МПа;
МПа;
для колеса ![]() МПа.
МПа.
Суммарное число циклов
перемены напряжений ![]() при постоянной нагрузке
определяется следующим образом [ф. 3.4]:
при постоянной нагрузке
определяется следующим образом [ф. 3.4]:
![]() ,
,
где с – число зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом, n – частота вращения, рассчитываемого зубчатого колеса (шестерни), об/мин, t – срок службы передачи, в часах.
Таким образом:
![]() циклов,
циклов,
![]() циклов.
циклов.
Базовое число циклов
перемены напряжений ![]() определим по графику,
представленному на рис. 3.3
определим по графику,
представленному на рис. 3.3
![]() циклов (HHB = 300).
циклов (HHB = 300).
![]() циклов (HHB = 300).
циклов (HHB = 300).
Так как ![]() определяем значение
определяем значение ![]() по формуле [c. 10]:
по формуле [c. 10]:
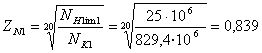 ;
;
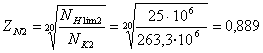 .
.
Используя полученные
данные, найдем допускаемые контактные напряжения ![]() , МПа:
, МПа:
![]() ;
;
![]() .
.
В
качестве допускаемого контактного напряжения 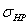 для косозубой передачи при
проектировочном расчете принимают условное допускаемое контактное напряжение,
определяемое по формуле:
для косозубой передачи при
проектировочном расчете принимают условное допускаемое контактное напряжение,
определяемое по формуле: 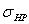 =
= 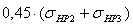 . При этом должно выполняться
условие:
. При этом должно выполняться
условие: 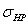 <
1,23
<
1,23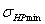 , где
, где 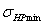 – меньшее из
значений
– меньшее из
значений 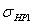 и
и
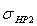 . В
противном случае принимают
. В
противном случае принимают 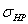 =
= 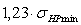 .
.
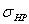 =
= 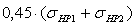 =
= 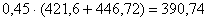 <
1,23*421,6
= 518,57
<
1,23*421,6
= 518,57
Полученные данные подставим в формулу по определению межосевого расстояния:
Полученное
межосевое расстояние округляется до стандартного значения [c.11]:
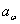 = 140 мм.
= 140 мм.
Ориентировочно определяем значение модуля (мм) [ф. 3.19]:
![]() мм.
мм.
По ГОСТ 9563-80 принимаем стандартный нормальный модуль [c. 17]:
m = 2 мм.
Зададимся
углом наклона 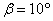 и определим суммарное zC,
число зубьев шестерни z2
и колеса z3 [ф.
3.20, ф. 3.21, ф. 3.22]:
и определим суммарное zC,
число зубьев шестерни z2
и колеса z3 [ф.
3.20, ф. 3.21, ф. 3.22]:
Тогда:
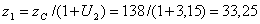 ; округляем до
целого: z1 = 33.
; округляем до
целого: z1 = 33.
z2 = zС – z1 = 138 – 33 = 105.
Действительное передаточное число и его погрешность определяется по формулам [ф. 3.23]:
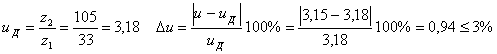 .
.
Уточняем значение угла b по формуле [ф. 3.24]:
![]() тогда
тогда ![]() .
.
Основные размеры шестерни и колеса:
Диаметры делительные шестерни и колеса определяются по формуле [ф. 3.25], мм:
Проверим полученные диаметры по формуле [ф. 3.26]:
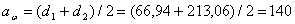 ,
,
что совпадает с ранее найденным значением.
Диаметры вершин зубьев определяются по формуле [ф. 3.27] с учетом того, что зубья изготовлены без смещения (х = 0), мм:
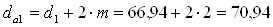 ,
,
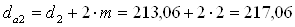 ;
;
диаметры впадин [ф. 3.28], мм:
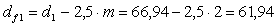 ,
,
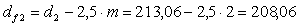 ;
;
основные диаметры, мм:
![]() ,
,
![]() ,
,
где делительный угол профиля в торцовом сечении:
![]() .
.
Ширина колеса определяется по формуле [ф. 3.29]:
![]() мм.
мм.
Ширина шестерни определяется по формуле [ф. 3.30], мм:
b1 = b2 + (5...10) = 44,1 + (5...10) = 49,1…54,1 мм.
Полученные значение ширины округляем до нормальных линейных размеров: b1 = 52 мм, b2 = 44 мм.
Определим окружную скорость зубчатых колес по формуле [ф. 3.31]:
![]() м/c..
м/c..
По окружной скорости колес назначаем 9-ю степень точности зубчатых колес [т. 3.4].
2. Проверочный расчет на контактную выносливость активных поверхностей зубьев
2.1. Расчет контактных напряжений
где
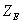 = 270 –
коэффициент, учитывающий механические свойства материалов сопряженных зубчатых
колес;
= 270 –
коэффициент, учитывающий механические свойства материалов сопряженных зубчатых
колес;
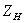 – коэффициент,
учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, для
косозубых передач:
– коэффициент,
учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, для
косозубых передач:
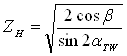 ;
; 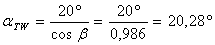 ;
; 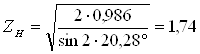 .
.
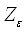 – коэффициент,
учитывающий суммарную длину контактных линий. Для косозубых передач:
– коэффициент,
учитывающий суммарную длину контактных линий. Для косозубых передач:
Коэффициент ![]() , учитывающий
распределение нагрузки между зубьями, выбирается по таблице в зависимости от
окружной скорости и степени точности по нормам плавности [т. 4.5]:
, учитывающий
распределение нагрузки между зубьями, выбирается по таблице в зависимости от
окружной скорости и степени точности по нормам плавности [т. 4.5]:
![]() = 1,13.
= 1,13.
![]() = 1,11;
= 1,11; ![]() ;
; ![]() = 140 мм (определено ранее).
= 140 мм (определено ранее).
Динамический коэффициент ![]() определяется
по таблице 5.1:
определяется
по таблице 5.1:
![]() .
.
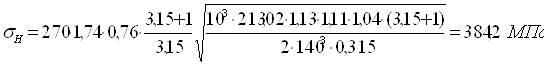
![]() условие выполнено.
условие выполнено.
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |