Курсовая работа: Проектирование и исследование механизмов поршневого насоса

.

Точку центра кулачка соединяем отрезком с каждой из точек 1 – 13 и измеряем углы, образуемые этими отрезками и соответствующими положениями коромысла – получаем значения угла передачи движения в определенных положениях кулачкового механизма (табл. 5). Строим график изменения угла передачи движения в масштабах μγ = 1°/мм и .

3.3 Профилирование кулачка

Из центра О проводим окружность радиусом . На дуге, описанной из центра Е радиусом ℓED, проводим разметку пути точки D согласно графику

β = β(t).

Обращаем движение. Из центра О радиусом ОЕ описываем дугу и в направлении обратном вращению кулачка откладываем от радиуса ОЕ углы φу, φд, φв, которые делим затем на равные части соответственно промежуткам графика β = β(t); обозначаем полученные точки деления 1' – 13'.

Из этих точек проводим дуги радиусом ℓED, а из центра О засекаем их радиусами ОD1 – OD13. Соединяя точки пересечения построенных дуг плавной кривой, получаем теоретический профиль кулачка.

Радиус ролика выбираем из следующих соображений:

rp ≤ 0,4∙ или rp ≤ 0,8∙ρmin,

где ρmin – минимальный радиус кривизны профиля кулачка.

Определяем графически ρmin = 6,64 мм.

0,4∙= 0,4∙44,28 = 17,71 мм,

0,8∙ρmin = 0,8∙6,64 = 5,32 мм.

Из двух значений принимаем наименьшее, тогда rp = 5,32 мм (в масштабе чертежа μℓ получаем  мм). Внутренняя огибающая окружностей, описанных радиусом ролика, центр которого перемещается по теоретическому профилю, образует искомый рабочий профиль кулачка.

4. Проектирование зубчатой передачи

4.1 Расчет привода машины

Дано:

числа зубьев колес Z1 = 21, Z2 = 47, Z6 = 12, Z7 = 18;

модули m1 = 5 мм; m2 = 5,5 мм;

передаточное отношение U1-5 = 15,85;

частота вращения двигателя nдв = 1530 об/мин;

межосевое расстояние

зацепления Z6 – Z7 неравносмещенное, коэффициент смещения Х выбирать из условия обеспечения заданного межосевого расстояния;

кинематическая схема привода представлена на рис. 5.

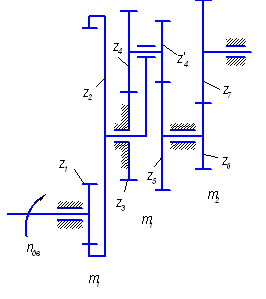
Рис. 5

Привод машины состоит из двух пар зубчатых колес с неподвижными осями и планетарной передачи. Определим передаточное отношение планетарной передачи .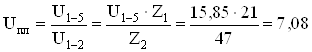

Передаточное отношение от водила к 5-му колесу определяется по формуле

,

.

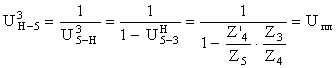Методом подбора разбиваем передаточное число следующим образом

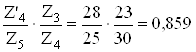, Z3 = 23, Z4 = 30, Z'4 = 23, Z5 = 25.

4.2 Расчет внешнего неравносмещенного зацепления с прямыми зубьями

Заданы следующие величины:

модуль зацепления m = 5,5 мм.

угол исходного профиля рейки α = 20º;

коэффициент высоты головки зуба исходного профиля ;

коэффициент радиального зазора ;

число зубьев шестерни Z6 = 12;

число зубьев колеса Z7 = 18;

межосевое расстояние aw = 85 мм.

Порядок проведения расчета. Делительные диаметры

;

.

Основные диаметры

;

.

Окружные делительный и основной шаги

;

.

Угол зацепления

;

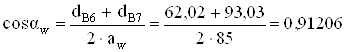αw = arccos 0,91206 = 24,208° = 24° 12' 30".

Суммарный коэффициент смещения

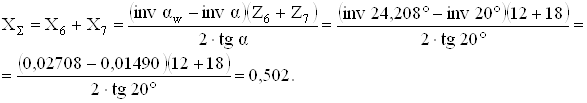
По блокирующему контуру [4, фиг. 32] разбиваем ХΣ на слагаемые и определяем Х6 = 0,383 и Х7 = 0,12.

Начальные диаметры

;

.

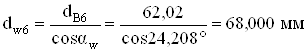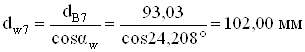Диаметры впадин зубьев

;

.

Диаметры вершин зубьев

;

.

Окружные толщины зубьев (о делительной окружности)

;

.

Проверка на заострение

;

;

;

;

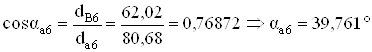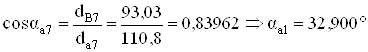Sa = 0,2 ∙ 5,5 = 1,1 мм, выполняется условие Sa6, Sa7 ≥ Sa, значит, заострения зубьев нет. По данным проведенных расчетов вычерчиваем зубчатое зацепление в масштабе μ'ℓ = 0,00025 м/мм.

4.3 Качественные показатели зацепления

1. Коэффициент перекрытия

;

;

.

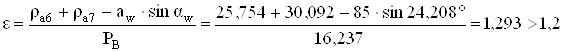2. Коэффициент удельного скольжения

;

;

, ;

; .

3. Коэффициент удельного давления в полюсе

;

.

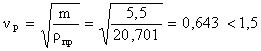Все показатели находятся в допускаемых пределах.

5. Силовой расчет механизма

Данные для расчета:

отношения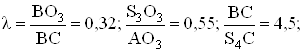

погонный вес q = 120 H/м;

сила полезного сопротивления Рпс = 158 Н;

Требуется определить давление в кинематических парах, уравновешивающую силу (момент).

Выбираем положение во время рабочего хода машины, в котором имеет место наибольшее ускорение рабочего органа – 7-е положение. Строим планы положения механизма в масштабе μℓ = 0,00175 , скоростей – μv = 0,01 , ускорений – μа = 0,05 .

Определяем положение центров тяжестей звеньев на планах

а) механизма

;

;

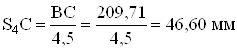б) скоростей

;

;

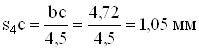в) ускорений

;

.

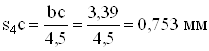Определяем веса звеньев

G3 = q∙ℓ3 = 120∙0,157 = 18,84 H;

G4 = q∙ℓ4 = 120∙0,367 = 44,04 H;

G5 = λ∙G4 = 0,32∙44,04 = 14,09 H.

Определяем силы инерции

;

;

.

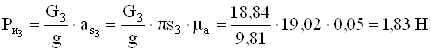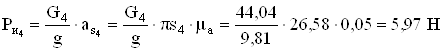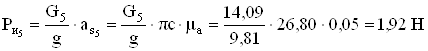Определяем моменты инерции звеньев

;

;

.

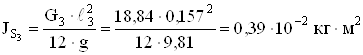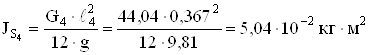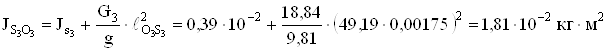Определяем угловые ускорения и моменты сил инерции звеньев

;

;

;

.

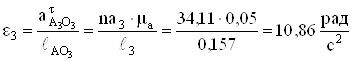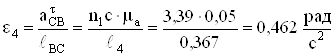Определяем плечи сил инерции

;

.

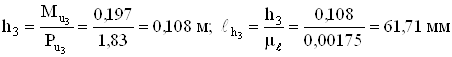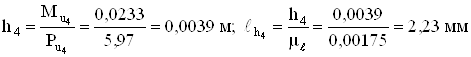Силовой расчет механизма начинаем с последней присоединенной группы Ассура – . На эту группу действует сила полезного сопротивления Рпс, сила тяжести поршня G5, сила инерции поршня Ри5, реакция стойки R05, вес шатуна G4, сила инерции шатуна Ри4, реакция отброшенного звена R34 ( и ).

Уравнение равновесия группы под действием этих сил имеет следующий вид

.

Величину и направление силы  можно найти из уравнения моментов всех сил, действующих на звено 4, относительно точки С

;

.

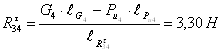Строим план сил в масштабе μР = 1 Н/мм и замеряем недостающие силы R05 = 33,15 Н; = 97,73 Н; = 97,67 Н.

Переходим к следующей группе Ассура . На нее действуют сила реакции предыдущей группы R43, сила инерции коромысла Ри3, вес коромысла G3, реакция стойки R03, реакция отброшенного звена R12.

Уравнение равновесия группы под действием этих сил имеет следующий вид

.

Величину и направление силы  можно найти из уравнения моментов всех сил, действующих на звено 3, относительно точки О3

;

.

.

Строим план сил и замеряем недостающие силы R03 = 103,27 Н.

Рассмотрим ведущее звено – кривошип. На него действует сила реакции предыдущей группы R21, реакция стойки R01, уравновешивающая сила Рур.

Уравнение равновесия группы под действием этих сил имеет следующий вид

.

Величину и направление силы Рур можно найти из уравнения моментов всех сил, действующих на звено 1, относительно точки О2

;

.

.

Строим план сил и определяем недостающие силы R01 = 59,29 Н.

Определим уравновешивающую силу с помощью рычага Жуковского.

Строим план скоростей и в соответствующих точках прикладываем внешние силы и силы инерции, поворачивая их на 90° по часовой стрелке. Составляем уравнение равновесия рычага

;

0.

Отсюда получаем

6. Расчет маховика

Для каждого положения механизма определяем приведенный к главному валу момент сил сопротивления, определяемый из условия равенства мощности приведенного момента и мощности силы полезного сопротивления

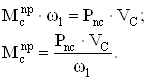
Для каждого положения механизма определяем приведенный к главному валу момент инерции, определяемый из условия равенства кинетических энергий

;

.

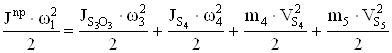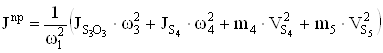Результаты всех расчетов и замеров сведены в таблицу 6.

Табл. 6

№	Mпр, Н∙м	Jпр, кг∙м2	ℓΔЕ, мм	, Дж	JMX + Jnp, кг∙м2	ω1, рад
0	0,00	0,0000	0,00	6,55	0,2214	7,69
1	2,46	0,0025	6,83	6,91	0,2239	7,86
2	3,87	0,0064	4,75	6,80	0,2278	7,73
3	4,97	0,0104	-3,52	6,37	0,2318	7,41
4	5,72	0,0128	-16,47	5,69	0,2342	6,97
5	5,96	0,0126	-31,96	4,87	0,2340	6,45
6	5,49	0,0095	-47,00	4,08	0,2309	5,95
7	3,88	0,0042	-57,42	3,54	0,2256	5,60
8	0,00	0,0000	-56,23	3,60	0,2214	5,70
9		0,0245	-42,17	4,34	0,2459	5,94
10		0,0732	-28,11	5,08	0,2946	5,87
11		0,0104	-14,06	5,81	0,2318	7,08

Строим графики Мпр и Jпр в масштабах μφ = 0,0175 рад/мм, μМ = 0,1 Н∙м/мм и μJ = 0,0008 кг∙м2/мм. Графическим интегрированием графика моментов получаем график приведенных работ (полюсное расстояние H = 30). Далее получаем график ΔЕпр(φ), его масштаб будет равен

.

Определяем минимальную и максимальную угловую скорость кривошипа

;

.

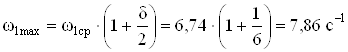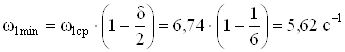Находим углы касательных к диаграмме

;

.

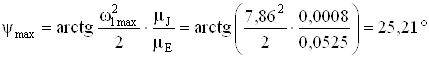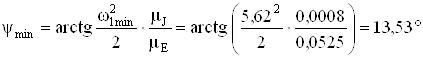Графически исключаем параметр φ и строим график ΔЕпр(J). Проводим к нему касательные под углами ψmax и ψmin. Точка пересечения касательных – новое начало координат графика.

Замеряем

JMX = 276,75∙0,0008 = 0,2214 кг∙м2;

Епр0 = 124,79∙0б0525 = 6,552 Дж.

Принимаем диаметр маховика dMX = 0,5 м, тогда вес обода будет

;

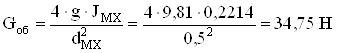вес маховика с ободом и спицами равен GMX = 1,3∙Gоб = 1,3∙34,75 = 45,18 Н.

Угловую скорость кривошипа в каждом положении механизма находим по формуле 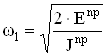, результаты расчета занесены в таблицу 6. График изменения угловой скорости строим в масштабе 0,1 (рад/с)/мм.

Определяем мощность двигателя по формуле

.

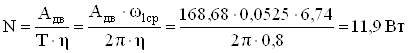Список литературы

1. Артоболевский И.И. Теория механизмов. – М., Издательство "Наука", 1965. – 776 с., ил.

2. Аллилуева Л.А., Езерская С.В., Кунивер А.С., Янченко Т.А. Методические указания к выполнению курсового проекта по теории механизмов и машин. 3-е изд., стереотипное. – Ижевск, Издательство ИжГТУ, 2004. – 72 с., ил.

3. Газизова З.С., Русаева В.А., Янченко Т.А. Задания для курсового проекта по теории механизмов и машин. Насосы и двигатели внутреннего сгорания. – Ижевск, Издательство ИжГТУ, 1980. – 32 с., ил.

4. Болотовская Т.П., Болотовский И.А., Смирнов В.Э. Справочник по корригированию зубчатых колес. – М.: Машгиз, 1962. – 216 с., ил.

5. Кореняко А.С. и др. Курсовое проектировании по теории механизмов и машин. – Киев, Издательство "Вища школа", 1970. – 332 с., ил.