 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Контрольная работа: Сопротивление материалов
![]() – момент сопротивления сечения
при изгибе; для сечения прямоугольной формы
– момент сопротивления сечения
при изгибе; для сечения прямоугольной формы
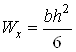 ,
,
где ![]() мм
мм![]() м – ширина прямоугольного
сечения балки;
м – ширина прямоугольного
сечения балки;
![]() мм
мм![]() м – высота прямоугольного сечения
балки;
м – высота прямоугольного сечения
балки;
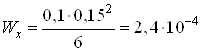 м3;
м3;
![]() – допускаемые напряжения при
изгибе; для дерева принимаем
– допускаемые напряжения при
изгибе; для дерева принимаем ![]() МПа.
МПа.
Проверяем несущую способность деревянной балки
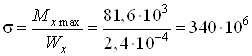 Па
Па![]() МПа,
МПа,
что значительно больше допускаемых напряжений. Следовательно, несущая способность балки не соблюдается.
Ответ: Прочность балки недостаточна.
Задача 5
Для двухопорной балки подобрать сечение двутавра из условия прочности.
Проверить прочность по
касательным напряжениям. Построить эпюры ![]() и
и ![]() для сечений, в которых
для сечений, в которых ![]() и
и ![]() . Нагрузку
принять состоящей: 1) из 80% постоянной, коэффициент перегрузки
. Нагрузку
принять состоящей: 1) из 80% постоянной, коэффициент перегрузки ![]() 2) из 20% временной,
коэффициент перегрузки
2) из 20% временной,
коэффициент перегрузки ![]() .
.
Данные для задачи своего варианта взять из табл. 5 и схемы на рис. 12.
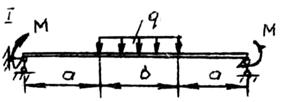
Таблица 5
| Вариант |
|
|
|
|
| м | ||||
| 49 | 4 | 4 | 12 | 6 |
Решение
1. Определяем действительные значения нагрузок, действующих на балку, используя метод расчета предельного состояния по несущей способности.
При этом расчетное усилие
в балке (в нашем случае ![]() и
и ![]() ) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
каждой нагрузке коэффициентов перегрузки. В результате получим
) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
каждой нагрузке коэффициентов перегрузки. В результате получим
![]() кН∙м;
кН∙м;
![]() кН/м.
кН/м.
2. Выполняем расчетную схему согласно исходных данных (рис.6,а).
Отбросим опоры и заменим
их влияние на балку опорными реакциями ![]() и
и ![]() (рис.6, б). Учитывая
симметричность конструкции, получим
(рис.6, б). Учитывая
симметричность конструкции, получим
![]() кН.
кН.
2. Балка имеет три
участка. Обозначим через ![]() расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил
расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил ![]() и изгибающих
моментов
и изгибающих
моментов ![]() ,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
Участок I ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
![]() кН∙м.
кН∙м.
При ![]() м
м
![]() кН;
кН;
![]() кН∙м.
кН∙м.
Участок II ![]() :
:
![]() ;
;
 .
.
При ![]() м
м
![]() кН;
кН;
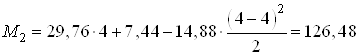 кН∙м.
кН∙м.
При ![]() м
м
![]() кН;
кН;
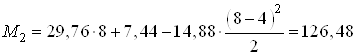 кН∙м.
кН∙м.
Так как на концах участка II поперечная сила меняет свой знак с плюса на минус, то на данном участке изгибающий момент принимает максимальное значение.
Из условия ![]() найдем абсциссу
найдем абсциссу ![]() сечения, в
котором действует изгибающий момент
сечения, в
котором действует изгибающий момент ![]() :
:
![]() ,
,
откуда
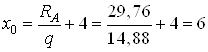 м.
м.
Тогда при ![]() м
м
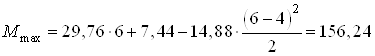 кН∙м.
кН∙м.
Участок III ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
![]() .
.
При ![]() м
м
![]() кН;
кН;
![]() кН∙м.
кН∙м.
3. По полученным
ординатам строим эпюры ![]() и
и ![]() балки (рис.6, в, г).
балки (рис.6, в, г).
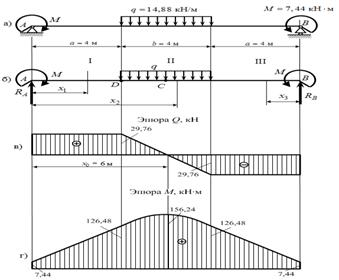
Рис. 3. Расчетные схемы к задаче 3
4. Определяем из условия прочности необходимый момент сопротивления сечения
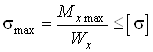 , (1)
, (1)
где ![]() – максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем
– максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем ![]() кН∙м;
кН∙м;
![]() – момент сопротивления сечения
при изгибе;
– момент сопротивления сечения
при изгибе;
![]() – допускаемые напряжения при
изгибе; принимаем для стали Ст3
– допускаемые напряжения при
изгибе; принимаем для стали Ст3
![]() МПа.
МПа.
Из выражения (1) находим требуемый момент сопротивления сечения
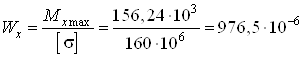 м3
м3![]() см3.
см3.
Для подбора сечения балки
в виде двутавра используем таблицу сортамента [1, с.283], откуда выбираем для
заданного сечения балки двутавр № 40, для которого ![]() см3. Перегрузка при
этом составит
см3. Перегрузка при
этом составит
![]() ,
,
что вполне допустимо (< 3%).
5. Построим эпюры ![]() и
и ![]() для сечений, в
которых
для сечений, в
которых ![]() и
и
![]() .
.
Сечение С (расположено посередине пролета ![]() ). В данном
сечении действуют только нормальные напряжения, так как поперечная сила равна
нулю.
). В данном
сечении действуют только нормальные напряжения, так как поперечная сила равна
нулю.
Нормальные напряжения вычисляем по формуле Навье
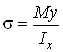 .
.
В данном сечении ![]() кН∙м,
кН∙м, ![]() кН.
кН.
Данные для двутавра №40: ![]() мм;
мм; ![]() мм;
мм; ![]() мм;
мм; ![]() мм;
мм; ![]() см2;
см2;
![]() см4;
см4;
![]() см3.
см3.
Обозначим характерные точки по высоте сечения (рис.7).
Точка 1:
![]() мм
мм![]() м;
м;
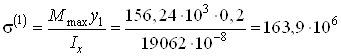 Па
Па![]() МПа.
МПа.
Поскольку изгибающий момент положительный, то точки 1 и 2 лежат в сжатой зоне и напряжения в этих точках имеют отрицательный знак.
Точка 2:
![]() мм
мм![]() м;
м;
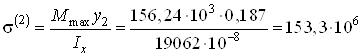 Па
Па![]() МПа.
МПа.
Точка 3:
![]() , так как
, так как ![]() . Ось, проходящая через точку 3,
называется нейтральной осью.
. Ось, проходящая через точку 3,
называется нейтральной осью.
Точки 4 и 5. В этих точках значения нормальных напряжений те же, что и в точках 2 и 1, только положительные, так как точки 4 и 5 лежат в растянутой зоне.
![]() МПа;
МПа;
![]() МПа.
МПа.
По полученным значениям
строим эпюру ![]() (рис.7).
(рис.7).
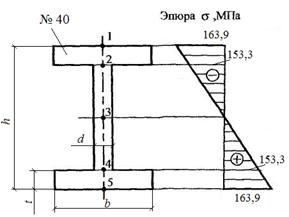
Рис.7. Эпюра нормальных напряжений в сечении С
Сечение D. Здесь действует максимальная
поперечная сила ![]() кН, а изгибающий момент равен
кН, а изгибающий момент равен ![]() кН∙м.
кН∙м.
Касательные напряжения ![]() вычисляем по
формуле
вычисляем по
формуле
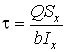 .
.
В точках 1 и 5 ![]() (рис.8).
(рис.8).
Точки 2 и 4. Вычисляем статический момент площади поперечного сечения
![]() ,
,
где ![]() – отсеченная часть
площади поперечного сечения;
– отсеченная часть
площади поперечного сечения;
![]() – координата центра тяжести
отсеченной площади.
– координата центра тяжести
отсеченной площади.
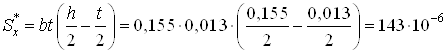 м3.
м3.
При ![]() мм
мм
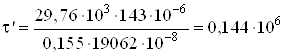 Па
Па![]() МПа.
МПа.
При ![]() мм
мм
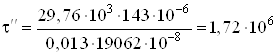 Па
Па![]() МПа.
МПа.
Точка 3. Это точка, расположенная на уровне нейтральной оси. Для нее имеем [2, с.257]
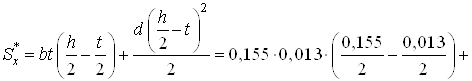
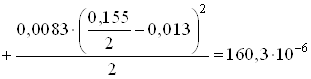 м3.
м3.
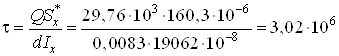 Па
Па![]() МПа.
МПа.
Нормальные напряжения в сечении D
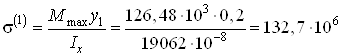 Па
Па![]() МПа (сжатие);
МПа (сжатие);
![]() МПа (растяжение).
МПа (растяжение).
Строим эпюры напряжений в сечении D (рис.8).
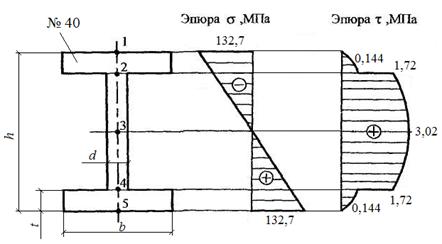
Рис. 8. Эпюра касательных напряжений в сечении А
Максимальное касательное
напряжение имеет место на нейтральной линии, то есть ![]() МПа.
МПа.
Допускаемое касательное
напряжение по 3-й теории прочности принимаем равным ![]() МПа.
МПа.
Следовательно, для балки двутаврового сечения
![]() МПа<96МПа
МПа<96МПа![]() .
.
Условие прочности выполняется.
Задача 6
Подобрать сечение
равноустойчивой центрально сжатой колонны из двух швеллеров или двутавров (в
зависимости от варианта выполняемой задачи), соединенных планками способом
сварки. Материал - сталь Ст3, расчетное сопротивление ![]() МПа. Данные для задачи своего
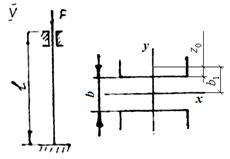
варианта взять из табл. 7 и рис. 13. Принять
МПа. Данные для задачи своего
варианта взять из табл. 7 и рис. 13. Принять ![]() .
.
| Вариант | Схема на рис. |
|
|
|
|
|
|
|
% от |
|||||||
| 49 | V | 6 | 0,6 | 30 | 70 | 1,3 | 1 |
Решение
1. Определяем действительное значение нагрузки, действующей на колонну, используя метод расчета предельного состояния по несущей способности.
При этом расчетное усилие
в колонне (в нашем случае ![]() ) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
данной нагрузке коэффициентов перегрузки. В результате получим
) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
данной нагрузке коэффициентов перегрузки. В результате получим
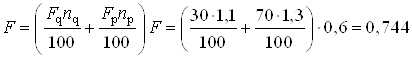 МН
МН![]() кН.
кН.
2. Равноустойчивость
колонны во всех направлениях будет обеспечена при равенстве моментов инерции
относительно осей ![]() и
и ![]() . Момент инерции сечения
относительно оси
. Момент инерции сечения
относительно оси ![]() не зависит от расстояния
не зависит от расстояния ![]() , поэтому
подбор сечения произведем, учитывая это обстоятельство.
, поэтому
подбор сечения произведем, учитывая это обстоятельство.
3. Принимая в качестве
первого приближения значение коэффициента ![]() , находим площадь поперечного
сечения колонны
, находим площадь поперечного
сечения колонны
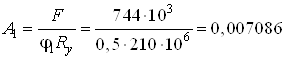 м2
м2![]() см2.
см2.
Из таблиц сортамента [1,
с.284] выбираем два швеллера № 30, для которых суммарная площадь сечения равна ![]() см2.
см2.
Наименьший радиус инерции из той же таблицы для составного сечения
![]() см.
см.
Определяем гибкость колонны
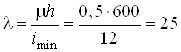 .
.
Коэффициент ![]() из табл.X.1[1] получаем равным
из табл.X.1[1] получаем равным ![]() .
.
Повторим расчет, принимая
![]() .
.
Далее находим
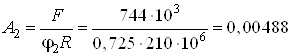 м2
м2![]() см2.
см2.
Из таблиц сортамента [1,
с.284] выбираем два швеллера № 20а, для которых суммарная площадь сечения равна
![]() см2;
см2;
![]() см.
Гибкость колонны при этом будет равна
см.
Гибкость колонны при этом будет равна
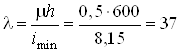 .
.
Коэффициент ![]() из табл.X.1 получаем равным
из табл.X.1 получаем равным ![]() .
.
Еще раз повторим расчет, приняв
![]() .
.
Далее получаем
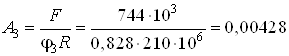 м2
м2![]() см2.
см2.
Выбираем швеллер № 18а.
Тогда ![]() см2;
см2;
![]() см.
см.
Гибкость
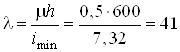 .
.
Коэффициент продольного
изгиба при этом равен ![]() .
.
Еще раз произведем расчет
![]() .
.
Далее получаем
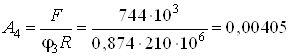 м2
м2![]() см2.
см2.
Выбираем швеллер № 18.
Тогда ![]() см2;
см2;
![]() см.
см.
Гибкость
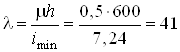 .
.
Коэффициент продольного
изгиба при этом равен ![]() и очень мало отличается от
и очень мало отличается от ![]() . Расчет
заканчиваем и принимаем швеллер № 18, для которого
. Расчет
заканчиваем и принимаем швеллер № 18, для которого ![]() см4;
см4; ![]() см4;
см4; ![]() см2.
см2.
Момент инерции сечения
колонны относительно оси ![]() равно
равно
![]() см4.
см4.
Момент инерции сечения
колонны относительно оси ![]() равно
равно
![]() .
.
Условие равноустойчивости имеет вид
![]() .
.
Подставляя сюда значения моментов инерции, получим
![]() ,
,
откуда находим расстояние
от центра тяжести швеллера до оси ![]()
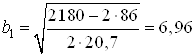 см.
см.
Определяем длину пластин
![]() см
см
Ответ: Сечение колонны: два швеллера № 18,
соединенные пластинами длиной ![]() см способом сварки.
см способом сварки.
Список использованной литературы
1. Степин П.А. Сопротивление материалов. М.: Высшая школа, 1983.
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов. М.: Высшая школа, 1989.
3. Ицкович Г.М. Сопротивление материалов. М.: Высшая школа, 1986.