 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Контрольная работа: Сопротивление материалов
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольника I;
до центра
тяжести прямоугольника I;
![]() см;
см;
![]() – площадь прямоугольника II;
– площадь прямоугольника II;
![]() см2;
см2;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольников II;
до центра
тяжести прямоугольников II;
![]() см;
см;
![]() – площадь треугольника III;
– площадь треугольника III;
![]() см2;
см2;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести треугольников III;
до центра
тяжести треугольников III;
![]() см;
см;
Подставляя числовые значения, получим
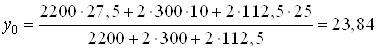 см.
см.
Кроме того, ![]() .
.
По этим данным наносим
точку ![]() –
центр тяжести сечения и проводим главные центральные оси сечения
–
центр тяжести сечения и проводим главные центральные оси сечения ![]() и
и ![]() .
.
2. Вычисляем главные центральные моменты инерции сечения:
![]() ;
; ![]() .
.
Для вычисления момента
инерции прямоугольника I ![]() относительно оси
относительно оси ![]() используем
формулу IV.10 [1, с.82]
используем
формулу IV.10 [1, с.82]
![]() ,
,
где ![]() – момент инерции прямоугольника
относительно собственной центральной оси
– момент инерции прямоугольника
относительно собственной центральной оси ![]() ;
;
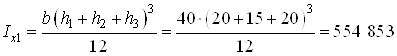 см4;
см4;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольника I
до центра
тяжести прямоугольника I
![]() см.
см.
Подставляя числовые значения, получим
![]() см4.
см4.
Аналогично находим моменты
инерции прямоугольников II и
треугольников III относительно оси ![]() :
:
![]() ,
,
где 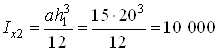 см4;
см4;
![]() см.
см.
![]() см4.
см4.
![]() ;
;
где 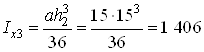 см4;
см4; ![]() см;
см;
![]() см4.
см4.
Суммарный момент инерции
относительно главной оси ![]()
![]() см4.
см4.
Точно также вычисляем
момент инерции относительно главной оси ![]() .
.
Для прямоугольника I
![]() ,
,
где 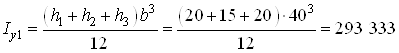 см4;
см4;
![]() см4.
см4.
Для прямоугольника II
![]() ,
,
где 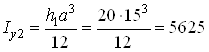 см4;
см4; ![]() см.
см.
![]() см4.
см4.
Для треугольника III
![]() ,
,
где 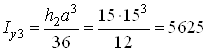 см4;
см4; ![]() см.
см.
![]() см4.
см4.
Суммарный момент инерции
относительно оси ![]()
![]() см4.
см4.
5. Вычерчиваем сечение в масштабе 1:5 с указанием на нем всех осей и размеров (рис.2).
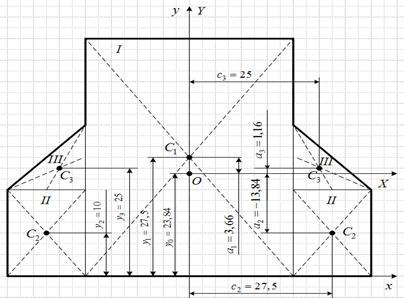
Рис.3. Сечение геометрической формы
a) Сечение, составленное из стандартных профилей проката.
1. Определяем координаты центра тяжести.
Для этого проводим
вспомогательные оси ![]() ,
, ![]() таким образом, что ось
таким образом, что ось ![]() совпадает с нижним
основанием полосы, а ось
совпадает с нижним
основанием полосы, а ось ![]() совпадает с осью симметрии фигуры.
Разбиваем сечение на три фигуры: прямоугольную полосу и два швеллера № 30, для
которых все необходимые данные выбираем из таблиц сортамента [1, c.284].
совпадает с осью симметрии фигуры.
Разбиваем сечение на три фигуры: прямоугольную полосу и два швеллера № 30, для
которых все необходимые данные выбираем из таблиц сортамента [1, c.284].
| Фигура | Размеры, см |
Площадь сечения |
Моменты инерции относительно собственных центральных осей, см4 |
|||
|
|
|
|||||
|
|
|
|||||
| Швеллер № 30 | 30 | 10 | 40,5 | 5810 | 327 | |
Находим геометрические характеристики прямоугольной полосы:
![]() см2;
см2;
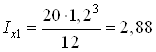 см4;
см4;
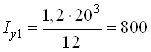 см4.
см4.
Поскольку ось ![]() является осью
симметрии сечения, то она будет являться главной центральной осью сечения
является осью
симметрии сечения, то она будет являться главной центральной осью сечения ![]()
Ординату центра тяжести сечения определяем по формуле
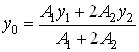 ,
,
где ![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести сечения прямоугольной полосы;
до центра
тяжести сечения прямоугольной полосы;
![]() см;
см;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести швеллеров;
до центра
тяжести швеллеров;
![]() см.
см.
Подставляя числовые значения, получим
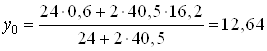 см.
см.
По этим данным наносим
точку ![]() –
центр тяжести сечения и проводим главные центральные оси
–
центр тяжести сечения и проводим главные центральные оси ![]() и
и ![]() .
.
2. Вычисляем главные моменты
инерции относительно осей ![]() и
и ![]() :
:
![]() ;
; ![]() .
.
Вычисляем момент инерции полосы
![]() относительно
оси
относительно
оси ![]()
![]() см4,
см4,
где ![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольника
до центра
тяжести прямоугольника
![]() см.
см.
Аналогично находим момент
инерции швеллера относительно оси ![]() :
:
![]() ,
,
где ![]() см;
см;
![]() см4.
см4.
Главный момент инерции
![]() см4.
см4.
Точно также вычисляем главный
момент инерции сечения относительно оси ![]() .
.
Для прямоугольной полосы
![]() см4.
см4.
Для швеллера
![]() ,
,
где ![]() см.
см.
![]() см4.
см4.
Суммарный момент инерции
относительно оси ![]()
![]() см4.
см4.
3. Вычерчиваем сечение в масштабе 1:2 с указанием на нем всех осей и размеров (в см) (рис.4).
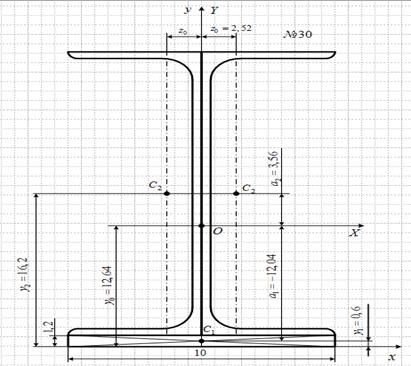
Рис.4. Сечение, составленное из стандартных профилей проката
Задача 4
Построить эпюры поперечных сил и изгибающих моментов от расчетной нагрузки. Проверить несущую способность деревянной балки.
Данные для задачи своего варианта взять из табл. 4 и схемы на рис. 11.
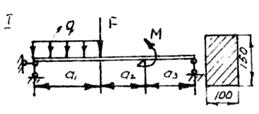
Таблица 4
| Вариант |
|
|
|
|
|
|
| м | ||||||
| 49 | 3 | 6 | 1 | 20 | 12 | 6 |
Решение
1. Выполняем расчетную схему согласно исходных данных (рис.5,а).
Отбросим опоры и заменим
их влияние на балку опорными реакциями ![]() и
и ![]() (рис.5, б).
(рис.5, б).
Определяем опорные реакции.
Составим сумму моментов
всех сил относительно точки ![]() :
:
![]() ;
; 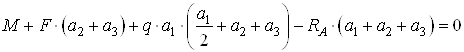 ,
,
откуда
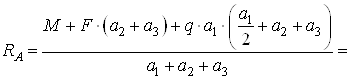
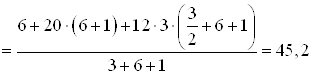 кН.
кН.
Составим сумму моментов
всех сил относительно точки ![]() :
:
![]() ;
; ![]() ,
,
откуда
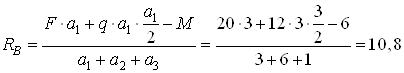 кН.
кН.
Проверка:
![]() .
.
Следовательно, реакции определены правильно.
2. Балка имеет три
участка. Обозначим через ![]() расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил
расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил ![]() и изгибающих
моментов
и изгибающих
моментов ![]() ,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
Участок I ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
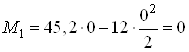 .
.
При ![]() м
м
![]() кН;
кН;
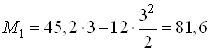 кН∙м.
кН∙м.
Поскольку уравнение
изгибающего момента – уравнение параболы, то для построения эпюры ![]() определим еще
одно значение момента:
определим еще
одно значение момента:
при ![]() м
м
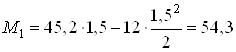 кН∙м.
кН∙м.
Участок II ![]() :
:
![]() ;
;
 .
.
При ![]() м
м
![]() кН;
кН;
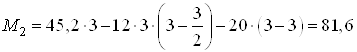 кН∙м.
кН∙м.
При ![]() м
м
![]() кН;
кН;
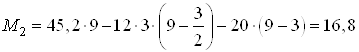 кН∙м.
кН∙м.
Участок III ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
![]() .
.
При ![]() м
м
![]() кН;
кН;
![]() кН∙м.
кН∙м.
3. По полученным
ординатам строим эпюры ![]() и
и ![]() балки (рис.5, в, г).
балки (рис.5, в, г).
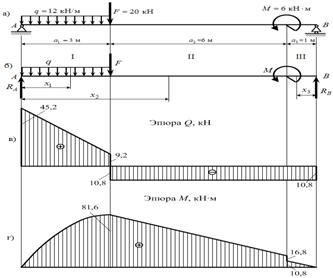
Рис. 5. Расчетные схемы к задаче 4
4. Условие прочности деревянной балки записывается в виде
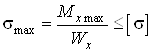 , (1)
, (1)
где ![]() – максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем
– максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем ![]() кН∙м;
кН∙м;
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |