 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Дипломная работа: Схема автоматического регулирования продолжительности выпечки с коррекцией по температуре во второй зоне пекарной камеры
![]()
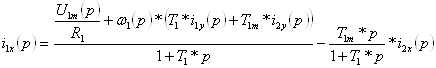 ;
;
![]() ;
;
(6.29)
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
По системе уравнений составим структурную схему асинхронного электродвигателя и механической части электропривода (графическая часть: лист 4).
6.2 Расчет основных параметров для функциональной схемы САУ
6.2.1 Определение потерь мощности в электродвигателе
Энергетическая диаграмма электродвигателя представлена на рис. 6.8.
Расчет потерь мощности будем вести для номинального режима работы электродвигателя.
Потребляемая электрическая мощность:
![]() .
.
Добавочные потери мощности:
![]() .
.
Механические потери мощности:
![]() .
.
Механическая мощность:
![]() .
.
Электромагнитная мощность:
![]() .
.
Потери в меди ротора:
![]() .
.
Потери в меди статора:
![]() .
.
Потери мощности в стали ротора для номинального режима можно пренебречь, т.к. частота тока ротора для номинального режима составляет fн=f1н*Sн=50*0.067=3.4 Гц, поэтому потери в стали ротора пренебрежимо малы.
Потери мощности в стали статора:
![]() .
.
6.2.2 Расчет параметров схемы замещения
Расчет параметров схемы замещения будем производить согласно методике, изложенной в [18]. Расчет производится на основании системы уравнений электромеханического преобразователя в системе координат α, β, жестко связанных со статором. При расчете воспользуемся схемой замещения фазы асинхронного двигателя (рис. 6.7.а).
Абсолютное скольжение:
![]() ,
,
где: ω1н – номинальная угловая скорость вращения вектора тока статора,
ωн – номинальная угловая скорость вращения ротора,
pп – количество пар полюсов.
Электромагнитный момент одной пары полюсов:
![]() .
.
Амплитуда векторов тока и напряжения:
![]() А,
А,
![]() А.
А.
Номинальный sinφ:
![]() .
.
Проекция вектора потокосцепления статора на оси α и β:
![]() ,
,
![]() .
.
Амплитуда вектора потокосцепления статора:
![]() .
.
Определим коэффициенты:
![]() ,
,
![]() ,
,
![]() ,
,
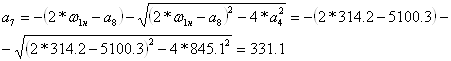 ,
,
![]() ,
,
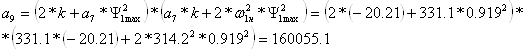 ,
,
![]() ,
,
![]() ,
,
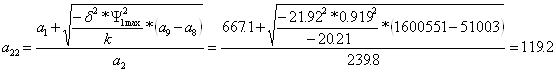
![]() ,
,
![]() .
.
Рассчитаем параметры схемы замещения АД. Индуктивность обмотки статора:
![]() .
.
Взаимоиндуктивность между обмотками статора и ротора:
![]() .
.
Индуктивность обмотки ротора:
![]() .
.
Активное сопротивление обмотки ротора:
![]() .
.
Индуктивность рассеяния обмотки статора:
![]() .
.
Индуктивность рассеяния обмотки ротора:
![]() .
.
6.3 Синтез регулятора момента
По способу регулирования максимального момента электроприводы с асинхронными короткозамкнутыми двигателями можно разделить на две группы:
1) с независимым регулированием частоты;
2) с зависимым регулированием частоты.
При независимом регулировании частоты
основными переменными являются амплитуда (![]() ) и частота (
) и частота (![]() ) подаваемого на статор
напряжения (системы скалярного управления), а при зависимом –
) подаваемого на статор
напряжения (системы скалярного управления), а при зависимом – ![]() и
и ![]() – частота тока ротора
(системы векторного управления). В электроприводах с независимым управлением
частотой регулирование максимального момента обычно осуществляется за счет
изменения амплитуды напряжения при заданной частоте, причем частота, как
правило, принимаются за независимую переменную. Регулирование, как правило,
осуществляется в функции одной или нескольких переменных, а предельные
реализации управляющих воздействий называют законами частотного регулирования.
– частота тока ротора
(системы векторного управления). В электроприводах с независимым управлением
частотой регулирование максимального момента обычно осуществляется за счет
изменения амплитуды напряжения при заданной частоте, причем частота, как
правило, принимаются за независимую переменную. Регулирование, как правило,
осуществляется в функции одной или нескольких переменных, а предельные
реализации управляющих воздействий называют законами частотного регулирования.
В реальных установках организовать управление по тому, или иному закону чисто программным способом невозможно, а поэтому вопрос выбора закона частотного регулирования необходимо решать не только с позиций достижимого результата, но прежде всего с позиции его регулируемости, которая, как правило, определяется возможностями программного обеспечения. Непосредственно измерить в асинхронной машине с короткозамкнутым ротором можно напряжение и ток статора и скорость ротора. При частичной разборке машины можно поместить на статор датчик ЭДС. Непосредственное же измерение момента на валу двигателя обычно не используется из=за сложностей с размещением датчиков и съемов сигналов. Формирование сигналов обратной связи по ЭДС с помощью датчиков тока и напряжения дает удовлетворительную точность при напряжении и токе, близких к синусоидальным. В противном случае векторное сравнение сигналов с различным гармоническим составом, меняющимся и от управляющего воздействия и от нагрузки, может привести к недопустимым погрешностям.
Наиболее просто в частотно-регулиремом электроприводе организовать измерение напряжения и тока статора. Но поскольку напряжение является регулируемой переменной, то использование таких сигналов компенсирует падение напряжения в вентильном преобразователе линеализует его регулировочную характеристику, но не определяет закона регулирования.
На основании вышесказанного для проектируемого электропривода выбираем систему стабилизации момента с положительной обратной связью по току [ 18].
Функциональная схема стабилизации максимального момента приведена на рис. 6.9.а, где: У – усилитель, ПЧ – преобразователь частоты, ДТ – датчик тока, а двигатель показан состоящим из двух частей М1 и М2. Поскольку нас интересует регулирование тока статора и момента при заданных uf и f1, то выход по скорости не показан.
Структурная схема контура тока в
статистических режимах приведена на рис. 6.9.б, где: ![]() – коэффициент передачи
преобразователя, по напряжению:
– коэффициент передачи
преобразователя, по напряжению:
![]() ;
;
![]() – коэффициент передачи двигателя
по току;
– коэффициент передачи двигателя
по току;
![]() – коэффициент передачи датчика
тока,
– коэффициент передачи датчика
тока,
![]() ;
;
kу – коэффициент усиления регулятора момента.
На основании структурной схемы для тока статора можно записать:
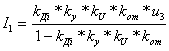 . (6.30)
. (6.30)
Из общего уравнения электромеханической характеристики (6.19) найдем:
![]() . (6.31)
. (6.31)
Подставив (6.31) в (6.30), получим уравнение электромеханической характеристики с положительной обратной связью в канале регулирования амплитуды напряжений:
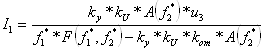 . (6.32)
. (6.32)
Подставив (6.32) в (6.20), запишем уравнение механической характеристики исследуемой системы:
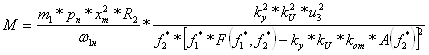 . (6.33)
. (6.33)
Уравнения (6.32), (6.33) неудобны для
расчетов, поскольку содержат две независимые входные переменные u3 и ![]() . В то же время система управления
частотно-регулируемым приводом строится таким образом, что без обратной связи
обеспечивается пропорциональный закон регулирования
. В то же время система управления
частотно-регулируемым приводом строится таким образом, что без обратной связи
обеспечивается пропорциональный закон регулирования ![]() , а обратная связь корректирует
закон изменения напряжения относительно частоты. В этом случае:
, а обратная связь корректирует
закон изменения напряжения относительно частоты. В этом случае:
![]() ,
(6.35)
,
(6.35)
где: u3н – номинальный сигнал задания.
С учетом (6.35) перепишем (6.32) и (6.33):
 , (6.36)
, (6.36)
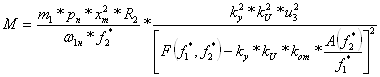 . (6.37)
. (6.37)
Аналитическое определение коэффициента усиления весьма сложно, что обусловлено сложностью функции в знаменателе (6.37), а также тем, что на входе системы сравнивается сигнал управления скоростью с сигналом управления по току статора, в общем случае не зависящем от скорости, что требует функциональной зависимости ky(u3).
Однако расчеты можно упростить без существенного снижения качества синтезирующей системы, исходя из следующих соображений:
1)
В реальных
системах нет необходимости точно соблюдать условие Мк=Мдоп,
а достаточно обеспечить Мк>Мтр во всем диапазоне
регулирования ![]() , где Мдоп и Мтр
– максимальный допустимый момент двигателя и требуемый по условию
перегружаемости момент. Мдоп ограничивается насыщением
магнитопровода машины.
, где Мдоп и Мтр
– максимальный допустимый момент двигателя и требуемый по условию
перегружаемости момент. Мдоп ограничивается насыщением
магнитопровода машины.
2)
При этом, даже
если на отдельных уровнях ![]() будем иметь Мк>Мдоп,
то перегрузки в автоматизированном электроприводе обычно снимают задержанными
обратными связями и другими средствами внешней информационной системы.
будем иметь Мк>Мдоп,
то перегрузки в автоматизированном электроприводе обычно снимают задержанными
обратными связями и другими средствами внешней информационной системы.
3)
Благодаря
сочетанию свойства асинхронного двигателя терять перегружаемость при снижении ![]() и свойства
положительной обратной связи по току увеличивать форсировку при снижении u3 появляется возможность отыскать такие оптимальные
значения ky=const, при которых обеспечивается условие Мк>Мтр
во всем диапазоне
и свойства
положительной обратной связи по току увеличивать форсировку при снижении u3 появляется возможность отыскать такие оптимальные
значения ky=const, при которых обеспечивается условие Мк>Мтр
во всем диапазоне ![]() . Это подтверждают и функции в
знаменателе (6.36) и (6.37), предельные значения которых будут
. Это подтверждают и функции в
знаменателе (6.36) и (6.37), предельные значения которых будут
![]() и
и 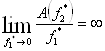 .
.
С учетом сказанного определение искомых параметров будем выполнять по следующей схеме:
1.
Исходя из условий
![]() и
и ![]() , строим
механические характеристики для
, строим
механические характеристики для ![]() , которые в дальнейшем будем
называть естественными характеристиками частотно-регулируемого электропривода.
Для построения используем (6.23) с подстановкой
, которые в дальнейшем будем
называть естественными характеристиками частотно-регулируемого электропривода.
Для построения используем (6.23) с подстановкой ![]() ,
, ![]() ,
, ![]() , предварительно найдя значения
членов формулы:
, предварительно найдя значения
членов формулы:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
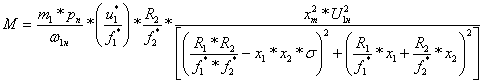 . (6.38)
. (6.38)
Результаты расчета представлены в виде графика на рис.6.10.
2. Для этих же частот построим предельные по условиям насыщения механические характеристики с потокосцеплением Ψm=const, выбранным за предельное. Эти характеристики построим по формуле из [18] при условии Iμ=Iμн=const:
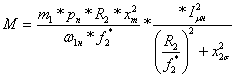 , (6.39)
, (6.39)
где номинальный намагничивающий ток определен по (6.21):
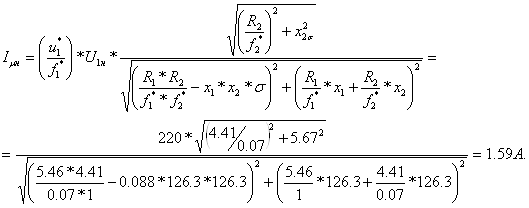
Результаты расчета представлены в виде графика (рис.6.10).
3.На характеристиках, соответствующих ![]() , проводим горизонталь ab (рис. 6.10), соответствующую
, проводим горизонталь ab (рис. 6.10), соответствующую
![]() .
.
Точкам любых характеристик с f1min=const,
лежащих на линии ab, будет
соответствовать условие ![]() .
.
4. На линии ab задаем Mтр=Mc<Mпред=Mн, т. е. Момент, обеспечивающий устойчивую работу электропривода на нижней скорости. По уравнению для механической характеристике при Ψm=const [18]:
![]() . (6.40)
. (6.40)
Найдем Iпред,
соответствующее Mпред при ![]() на линии ab и выбранном Iμ:
на линии ab и выбранном Iμ:
 .
.
Учитывая, что при ![]() и
и ![]()
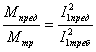 , (6.41)
, (6.41)
найдем ток статора в расчетной точке:
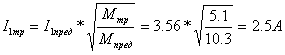 .
.
Подставив найденный ток в (6.36), найдем искомый коэффициент усиления ky:

6.4 Построение статических характеристик электропривода
По уравнению (6.19) построим естественную электромеханическую характеристику электропривода:
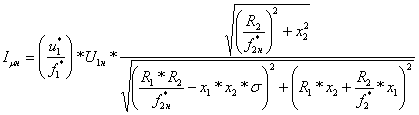 . (6.42)
. (6.42)
Результаты расчета представлены в виде графика (рис.6.11).
Естественная механическая характеристика была построена в пункте 6.3.
Для построения искусственных статических характеристик на основании структурной схемы запишем выражение для напряжения:
![]() . (6.43)
. (6.43)
Подставим в (6.43) выражение для тока (6.19):
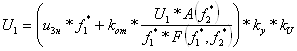 . (6.44)
. (6.44)
Из уравнения (6.44) выразим U1 и запишем выражение:
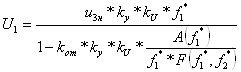 . (6.45)
. (6.45)
При построении искусственных статических характеристик следует учесть ограничение подводимого к электродвигателю напряжения. Напряжение U1 будем ограничивать на уровне U1max=1.1 U1н.
Составим систему уравнений для построения искусственных механических и электромеханических характеристик электропривода:
![]()
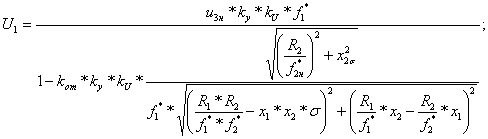
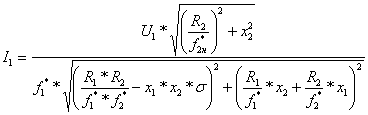 ;
;
(6.46)
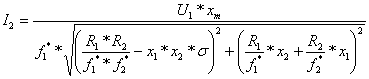 ;
;
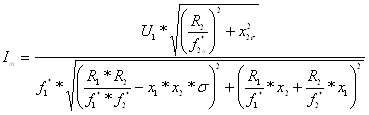 ;
;
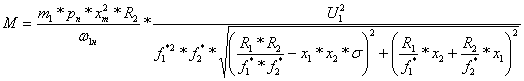 .
.
Построим по системе (6.46)
статические характеристики для двух скоростей ![]() и
и ![]() . Результаты расчета представлены
в виде графиков (рис. 6.11, 6.12).
. Результаты расчета представлены
в виде графиков (рис. 6.11, 6.12).
6.5 Проверка электродвигателя по нагреву при работе на нижней скорости
Известно, что у само вентилируемых двигателей ухудшаются условия охлаждения при снижении частоты вращения. Поэтому необходимо проверить, соблюдаются ли условия по нагреву при работе на нижней скорости диапазона регулирования. Расчет допустимого момента по условиям нагрева будем
производить по методике, изложенной в [8].
Известно, что лимитирующей по нагреву частью асинхронного короткозамкнутого двигателя в установившемся режиме является изоляция обмотки статора. Среднее установившееся превышение температуры обмотки статора может быть определено по методу эквивалентных потерь, согласно которому уравнение теплового баланса записывается следующим образом:
![]() , (6.47)
, (6.47)
где: τ∞ – установившееся превышение температуры статора;
![]() – теплоотдача, зависящая от
угловой скорости;
– теплоотдача, зависящая от
угловой скорости;
![]() – коэффициенты внешнего
подогрева, учитывающие долю внешних потерь, участвующих в нагревании обмотки
статора, в общем случае зависящие от скорости.
– коэффициенты внешнего
подогрева, учитывающие долю внешних потерь, участвующих в нагревании обмотки
статора, в общем случае зависящие от скорости.
![]() ,
(6.48)
,
(6.48)
![]() , (6.49)
, (6.49)
![]() ,
,
![]() .
.
Распишем выражения для ΔPM1, ΔPM2, ΔPcm:
 (6.50)
(6.50)
![]() ; (6.51)
; (6.51)
![]() , (6.52)
, (6.52)
где: ΔPсmвн – номинальные потери в стали на вихревые токи;
φ – относительное значение потока;
ΔPсmгн – номинальные потери в стали на гистерезис.
Перепишем (6.42) в виде:
![]() . (6.53)
. (6.53)
Для номинального режима уравнение (6.53) примет вид:
![]() ,
,
или
![]() , (6.54)
, (6.54)
где: hτ – доля эквивалентных греющих потерь при номинальном режиме.
Поделив почленно (6.53) на (6.54), получим уравнение теплового баланса при частотном управлении в относительных единицах:
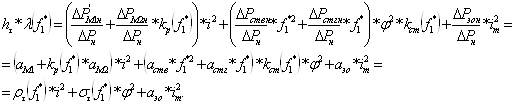 (6.55)
(6.55)
Примем допущение [8]:
![]() , (6.56)
, (6.56)
где: μ – относительное значение момента.
Подставим (6.56) в (6.55) и выразим μ:
 . (6.57)
. (6.57)
Определим значения постоянных коэффициентов:
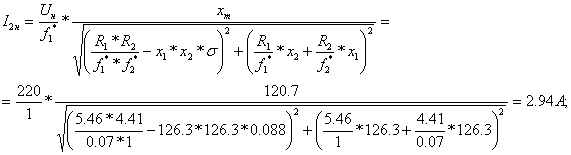
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Примем из [8] ![]() , тогда:
, тогда:
![]() ,
,
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |