Учебное пособие: Инфракрасная спектроскопия и спектроскопия кругового дихроизма. Методы определения вторичной структуры белков

Эту проблему частично можно разрешить, заменив метод наименьших квадратов моделью, применение которой, на первый взгляд, не вполне оправдано и адекватно, но зато приводит к устойчивому к экспериментальной ошибке результату даже в случае большого числа параметров. Применение такой стабилизирующей модели позволяет подойти к анализу спектров КД с другой стороны. А именно, появляется возможность прямого представления спктра КД исследуемого белка в виде линейной комбинации базисных спектров. Таким образом удается полностью избежать проблемы, связанной с определением эталонных спектров отдельных структурных классов и проводить более гибкий и точный анализ с использованием реальных белковых спектров.

Рассмотрим данный метод более подробно. Предположим, что нам удалось представить спектр КД исследуемого белка в виде линейной комбинации спектров  базисных белков, структура которых известна из рентгеноструктурного анализа. Обозначим число этих спектров через  (в данном методе =16). Тогда можем записать:

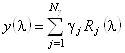, (1.2.9)

где  - спектр КД (эллиптичность) исследуемого белка.

Обозначим долю аминокислот j-ого базисного белка в i-ом структурном классе через , тогда базисные спектры могут быть представлены в виде суперпозиции  идеализированных эталонных спектров , соответствующих отдельным структурным классам:

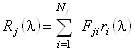. (1.2.10)

Аналогично для спектра КД исследуемого белка:

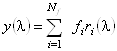. (1.2.11)

Подставляя равенства (1.2.10) и (1.2.11) в уравнение (1.2.9), получим связь искомых коэффициентов  с известными (из рентгеноструктурного анализа) коэффициентами :

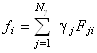. (1.2.12)

Проблема заключается в определении коэффициентов  в разложении (1.2.9). В подобных задачах широко применяется метод наименьших квадратов, определяющий коэффициенты  из следующего условия:

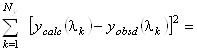 minimum (1.2.13)

с ограничениями

и. (1.2.14)

Здесь  и  - экспериментальное и рассчитанное по формуле (1.2.9) значения для эллиптичности на длине волны ,  - число точек в спектре.

Согласно теореме Гаусса-Маркова, среди линейных несмещенных оценок оценка, получаемая с помощью метода наименьших квадратов, является наиболее эффективной в том смысле, что рассчитанные с его помощью коэффициенты  наиболее близки к своим истинным значениям. Однако, при больших значениях  метод наименьших квадратов становится крайне неустойчивым к экспериментальной ошибке. Повышение стабильности метода за счет снижения величины , в свою очередь, также приводит к заметной ошибке.

Авторы метода [4] нашли выход в использовании вместо метода наименьших квадратов линейной смещенной оценки, определяемой следующим условием:

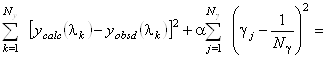 minimum. (1.2.15)

Эта оценка является смещенной и, следовательно, приводит к систематической ошибке. Тем не менее при больших значениях  она дает значения  более близкие реальным, чем получаемые с помощью метода наименьших квадратов. Очевидно, что уравнение (1.2.15) также необходимо дополнить условиями (1.2.14).

Рассмотрим критерий (1.2.15) более подробно. При a=0 мы получаем обычный метод наименьших квадратов, не пригодный в нашем случае. При a>0 второй член в левой части (1.2.15) является регуляризатором. Он стабилизирует решение, поддерживая коэффициенты  малыми (близкими к 1/). Тем не менее, если некоторый спектр  содержит компоненты, которые хорошо аппроксимируют , это ограничение не будет иметь такой силы, так как минимизация левой части уравнения (1.2.15) сможет быть достигнута в большей степени уменьшением первого члена, чем второго, что приводит к наиболее оптимальному значению . Таким образом получается очень гибкая, но стабильная модель, которая самостоятельно выбирает из большого набора базисных спектров те, которые аппроксимируют данные наилучшим образом. В случае анализа спектров КД белков уравнению (1.2.15) можно дать следующую интерпретацию. Поскольку априори нельзя сказать, какой из спектров  будет аппроксимировать  лучше, ни один из них не имеет преимущества, и все коэффициенты  полагаются приблизительно равными, близкими к 1/ (смотри условия (1.2.14)).

При возрастании параметра a точность аппроксимации экспериментальных данных падает за счет уменьшения эффективного числа степеней свободы, соответствующего числу свободных параметров в обычном методе наименьших квадратов. Обычно при малых a это происходит медленно, но когда этот параметр становится слишком большим, число степеней свободы становится таким малым, что коэффициенты  становятся равными 1/, и метод полностью теряет свою гибкость. Выбор параметра a определяется оптимальным компромиссом между гибкостью и стабильностью модели, тем самым давая наилучшие значения . Авторы данного метода осуществляли выбор a с помощью автоматического статистического теста на относительное увеличение отклонения аппроксимирующего спектра (реконструированного из спектров эталонных белков) от экспериментальных данных при увеличении этого параметра.

Если при анализе спектра КД белка нам известно, что среди белков базисного набора есть белки, структурно схожие с исследуемым, то в уравнение (1.2.15) можно ввести эти данные с помощью различного взвешивания отдельных членов второй суммы этого уравнения, тем самым давая соответствующим коэффициентам  большую свободу изменения. Однако сделать это объективно и количественно довольно сложно, поэтому авторы метода не пользовались этим. Как показывают эксперименты, в случае структурной схожести белков соответствующие коэффициенты  автоматически выбираются наибольшими без какой-либо дополнительной информации.

Метод "ортогональных спектров" [5,6]. Основой данного метода является метод собственных векторов многокомпoнентного матричного анализа. Он позволяет проводить быструю обработку больших наборов данных с помощью формирования из них ортогональных компонент в виде собственных векторов с соответствующими собственными значениями.

Этот метод использует в качестве базисных спектры КД 16 белков с известной вторичной структурой в диапазоне 178-260 нм с интервалом в 2 нм (всего по 42 точки в каждом из 16 спектров). Пусть С - прямоугольная матрица размером 1642, содержащая в качестве строк спектры КД эталонных белков. Умножая ее на свою транспонированную матрицу, получим симметричную квадратную матрицу CCT размером 1616. Приведем эту матрицу к диагональному виду с помощью ортогональной матрицы U (1616):

 (CCT) U = UE.  (1.2.16)

Матрица U будет состоять из 16 собственных векторов, а диагональная матрица Е - из 16 собственных значений матрицы CCT. Рассмотрим матрицу B, определяемую выражением

B = UTC. (1.2.17)

Это прямоугольная матрица, которая, также как и матрица исходных спектров КД базисных белков, имеет размер 1642. Ее строки можно использовать в качестве 16 новых ортогональных базисных спектров КД, каждый из которых представляет собой линейную комбинацию исходных белковых спектров. Разложение произвольного спектра КД по этим новым базисным спектрам, вместо исходных, оказывается более удобным, поскольку “значимость" каждого их них в этом разложении, то есть степень, в которой он представляет исходный набор базисных спектров, пропорциональна квадратному корню из соответствующего собственного значения. Из этого следует, что любой неполный набор из ортогональных базисных спектров, выбранный таким образом, что соответствующие им собственные значения максимальны, будет описывать произвольный белковый спектр КД лучше, чем любой неполный набор из исходных спектров базисных белков.

Ошибка, возникающая при аппроксимации экспериментального белкового спектра КД с помощью неполного набора наиболее “значимых" ортогональных базисных спектров, определяется следующей формулой:

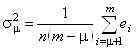. (1.2.18)

Здесь s - среднее квадратичное отклонение, n - число точек в спектре, m - число базисных спектров в исходном наборе,  - число ортогональных базисных спектров в неполном наборе, используемом для реконструкции произвольного белкового спектра, а  - собственные значения, расположенные в ряд в порядке убывания их величины. Случайная ошибка, связанная с погрешностью измерений при снятии спектров КД эталонных белков, приблизительно равна 0.3 единицы De. Сравним ее со значениями s, рассчитанными по формуле (1.2.18) для разных значений m (при m=16):

m	s, ед. De
3	0.38
4	0.24
5	0.17
6	0.12

Из приведенной таблицы видно, что четыре ортогональных базисных спектра дают значение s, нe превышающее уровень случайной ошибки. Но эксперименты показывают, что форма реконструированного таким образом спектра плохо совпадает с реальной. Пять ортогональных базисных спектров дают значение s, в два раза меньшее уровня случайной ошибки, и при этом хорошо воспроизводят форму спектра. Шесть ортогональных базисных спектров дают лишь незначительное улучшение.

Это объясняется тем, что оставшиеся базисные спектры представляют собой ни что иное, как “шум”, и их учет приводит лишь к увеличению ошибки при вычислениях. Авторы данного метода использовали для вычислений пять "наиболее значимых" ортогональных базисных спектров (m=5), полагая это количество оптимальным. Эти спектры представлены на рисунке 1.2.2.

Из выражения (1.2.17) следует, что

С = UB. (1.2.19)

Восстанавливая по сокращенному набору ортогональных базисных спектров исходный набор базисных спектров КД, можем написать:

, (1.2.20)

где  - исходные базисные спектры (i=1,., 16; k=1,.,42), а- - пять "наиболее значимых" ортогональных базисных спектров. Эксперименты по воспроизведению исходных белковых спектров по формуле (1.2.20) показывают, что среднеквадратичная ошибка при этом составляет от 0.08 до 0.25, что является весьма хорошим показателем.

Представим данные рентгеноструктурного анализа для 16 базисных белков в виде матрицы S размером 168, содержащей величины относительного содержания в каждом из белков восьми структурных элементов: спиральной структуры, включая a - и 310-спирали, антипараллельной и параллельной b-структуры, b-изгибов I, II, III типов, других видов b-изгибов и оставшейся (“неупорядоченной”) структуры.

Как можно предполагать из того факта, что исходный набор базисных спектров может быть полностью восстановлен но основе лишь пяти спектров ортогонального базисного набора, спектры КД белков в диапазоне от 178 до 260 нм содержат в себе информацию лишь о пяти независимых типах вторичной структуры.

С точки зрения независимости спектров КД в качестве таких типов вторичной структуры могут быть приняты комбинации обычных типов вторичной структуры (a-спирали, b-структуры и т.д.), соответствующие пяти "наиболее значимым" ортогональным базисным спектрам.

Если для ортогональных базисных спектров также ввести матрицу структурных данных D (168), то аналогично формуле (1.2.19) можно записать

S = UD (1.2.21)

Как показывает эксперимент, структурная матрица S может быть полностью восстановлена на основе лишь пяти комбинаций элементов вторичной структуры матрицы D, соответствующих пяти "наиболее значимым" ортогональным базисным спектрам. Таким образом, эти комбинации обычных типов вторичной структуры являются (с точки зрения независимости спектров КД) независимыми вторичными "суперструктурами":

Номер "супер-структуры"	a, 310	b ­¯	b ­­	b-изг. I	b-изг. II	b-изг. III	b-изг. др.	Ост. типы
1	1.77	0.30	0.20	0.16	0.07	0.12	0.14	1.06
2	0.56	-0.47	-0.06	-0.04	-0.07	-0.01	-0.09	-0.76
3	0.06	0.38	-0.12	0.01	0.02	0.01	0.01	-0.18
4	0.00	0.06	0.27	-0.04	-0.02	0.00	0.03	-0.06
5	-0.01	-0.01	0.02	0.16	0.02	0.05	0.00	-0.03

Следовательно, восемь рассматриваемых в данном методе стандартных структурных классов, вообще говоря, не являются строго независимыми, так как все они также могут быть описаны с помощью пяти независимых “суперструктур”, описанных выше.

Страницы: 1, 2, 3, 4