 | |
МЕНЮ
- Главная
- Языкознание филология
- Финансовые науки
- Управленческие науки
- Товароведение
- Технология
- Теплотехника
- Теория организации
- Теория государства и права
- Таможенная система
- Схемотехника
- Строительство
- Страхование
- Статистика
- Религия и мифология
- Психология и педагогика
- Промышленность производство
- Медицинские науки
- Медицина
- Краеведение и этнография
- Компьютерные науки
- История
- Искусство и культура
- Информатика
- Инвестиции
- Издательское дело и полиграфия
- Зоология
- Журналистика
- Естествознание
- Деньги и кредит
- Делопроизводство
- Гражданское право и процесс
- Государство и право
- Геополитика
- Геология
- Геодезия
- География
- Военная кафедра
- Ветеринария
- Валютные отношения
- Бухгалтерский учет и аудит
- Ботаника и сельское хоз-во
- Биржевое дело
- Биология и химия
- Биология
- Безопасность жизнедеятельности
- Банковское дело
- Астрономия
- Астрология
- Архитектура
- Арбитражный процесс
- Административное право
- Авиация и космонавтика
- Карта сайта
Курсовая работа: Водяной насос
Проверка: 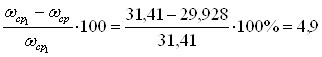 %
%
2. Динамический анализ рычажного механизма
Силовой расчет механизма
Задачей силового анализа является определение при заданном законе движения неизвестной внутренней силы, то есть усилия (реакции) в кинематических парах. Эта задача решается с применением принципа Даламбера. Силовой расчет плоских рычажных механизмов выполняется по группам Асура в порядке обратном их присоединения к входному звену.
2.1 Определение углового ускорения звена приведения
Угловое ускорение определяем из дифференциального уравнения машинного агрегата:
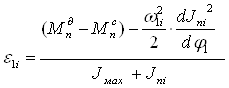 ;
;
где 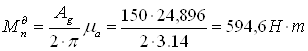
Расчет производим для 10-го положения механизма (Мпр10 - максимальный).
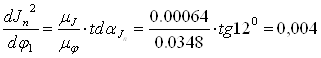
![]() -угол наклона касательной
к кривой графика
-угол наклона касательной
к кривой графика ![]() к оси абсцисс в
исследуемой точке.
к оси абсцисс в
исследуемой точке.
Подставляем ранее определенные значения и получим:
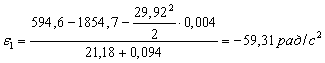
Ведущее звено движется замедленно.
2.2 Определение линейных и угловых скоростей, ускорений точек и звеньев механизма
Для
построения плана механизма в 10-ом положении примем масштабный коэффициент ![]() м/мм
м/мм
Для построения плана скоростей определим скорость точки В.
![]() м/с
м/с
Приняв отрезок pb=340 мм, определим масштабный коэффициент.
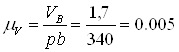 м/(с·мм)
м/(с·мм)
Построение плана ведется в соответствии с векторными уравнениями рассмотренными в положении №10. Тогда действительные скорости:
![]() м/c
м/c
![]() м/c
м/c
![]() с-1
с-1
![]() м/c
м/c
Направление ![]() получим,
поместив вектор
получим,
поместив вектор ![]() в точку С звена 2 и рассмотрев
поворот звена под его действием относительно точки В.
в точку С звена 2 и рассмотрев
поворот звена под его действием относительно точки В.
Так как кривошип вращается неравномерно, ускорение точки В кривошипа равно:
![]()
![]()
![]()
Выбираем
масштабный коэффициент для ускорения ![]() .
.
Вычисляем
отрезки изображающие ![]() и
и ![]()
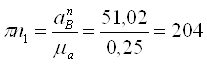 мм,
мм,
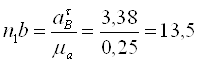 мм
мм
Из полюса ![]() откладываем
откладываем ![]() ║ АВ направленный к
центру вращения, отрезок
║ АВ направленный к
центру вращения, отрезок ![]() ┴
АВ в направлении
┴
АВ в направлении ![]() .
.
Ускорение точки С найдем, решив графически систему векторных уравнений.
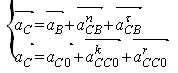
где
нормальная составляющая ![]() ║
СВ и равна:
║
СВ и равна:
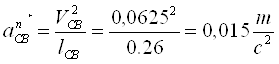
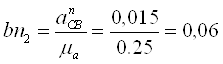 мм
мм
тангенциальная
составляющая ![]() ┴ СВ.
┴ СВ.
Точка ![]() принадлежит стойке,
поэтому
принадлежит стойке,
поэтому ![]() ║.
║.
Положение
точки ![]() найдем по теореме подобия:
найдем по теореме подобия:
![]() мм
мм
Тогда действительные ускорения точек и звеньев равны:
![]() м/с2
м/с2
![]() м/с2
м/с2
![]() м/с2
м/с2
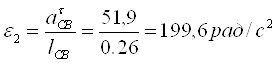
Направление ![]() получим, помещая
получим, помещая ![]() в точку С и рассматривая
поворот звена 2 под его действием относительно точки В. Звено движется ускоренно.
в точку С и рассматривая
поворот звена 2 под его действием относительно точки В. Звено движется ускоренно.
2.3 Расчет сил, действующих на звенья механизма
Определим силы тяжести звеньев, главные векторы и главные моменты сил инерции звеньев.
Звено 1: ![]()
![]() - т.к. кривошип
уравновешен.
- т.к. кривошип
уравновешен.
![]()
Звено 2: ![]()
![]()
![]()
Звено 3: ![]()
![]()
![]()
Ф2= ![]() ; Ф3=
; Ф3= ![]()
2.4 Определение значений динамических реакций в кинематических парах групп Ассура
Fc[10] = 33221,2 H
Отсоединим
группу Асура (2; 3). Приложим все известные внешние силы, главный вектор сил
инерции Fи2 и главный момент сил инерции Ми2, а вместо отброшенных звеньев 1 и стойки 0
приложим реакции F21 и
F30, причем неизвестного по
величине F21 представим как сумму: ![]() , а реакцию F30 направим перпендикулярно
направляющей ползуна.
, а реакцию F30 направим перпендикулярно
направляющей ползуна.
Определим
реакцию ![]() из условия
из условия ![]() для звена 2
для звена 2
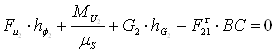

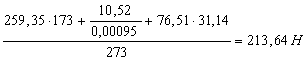
Для
определения составляющей ![]() и реакции F30 запишем на основании
принципа Даламбера векторное уравнение статики для групп Ассура (2; 3)
и реакции F30 запишем на основании
принципа Даламбера векторное уравнение статики для групп Ассура (2; 3)
![]()
Выбираем
масштабный коэффициент ![]() Н/мм
Н/мм
Определим чертежные отрезки, изображающие силы на чертеже:
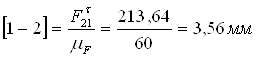
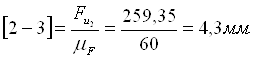
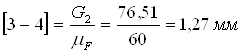
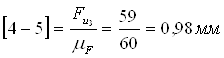
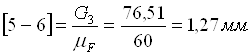
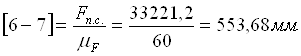
Строим план сил группы Асура (2; 3)
Из плана определяем:
![]()
![]()
![]()
Переходим к
силовому расчету механизма 1 класса. В точку В приложим реакцию ![]() . К звену 1 прикладываем
главный момент сил инерции
. К звену 1 прикладываем
главный момент сил инерции ![]() и
движущий момент. Рассмотрим равновесие звена 1 относительно точки А.
и
движущий момент. Рассмотрим равновесие звена 1 относительно точки А.
![]()
Из плана сил
определяем: ![]() .
.
2.5 Оценка точности расчетов
Находим относительную погрешность:
![]()
![]()
594,6 + 1258,8 – 33600·58,05·0,00095 = 1853,4 – 1852,9 = 0,5 ≈ 0.
3. Синтез зубчатого механизма
Исходные данные:
Параметры планетарного редуктора:
U1H = 5,5; k = 4; m1 = 7 мм.
Параметры открытой зубчатой передачи:
Z4 = 15; Z5 = 28; m = 12 мм.
Параметры исходного контура по ГОСТ 16532–70:
a = 20 град; ha* = 1; c* = 0,25.
3.1 Подбор чисел зубьев
Подбор чисел
зубьев и числа сателлитов производим с учетом условия соосности:![]() воспользуемся формулой
Виллиса с учетом
воспользуемся формулой
Виллиса с учетом![]()
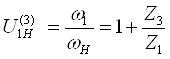 ;
; 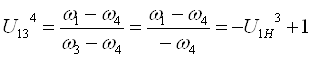
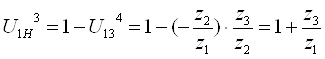 ;
; 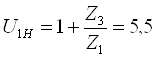
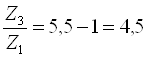
Подбор зубьев производим путем подбора с учетом ряда ограничений:
Для колес с внешними зубьями: Z1 ≥ Zmin = 17
Для колес с внутренними зубьями: Z3 ≥ Zmin = 85 при ha* = 1
Принимаем Z1 = 24, Z3 = (U1H – 1)*Z1 = 4.5 * 24 = 108
Число зубьев Z2 определяем из условия соседства:
Z1 + Z2 = Z3 – Z2
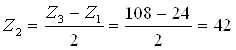 - условие целостности выполняется.
- условие целостности выполняется.
Сборка нескольких сателлитов должна выполняться без натягов при равных окружных шагах между ними. Оно выражается следующим соотношением:
![]() , где Ц = 1, 2, 3, … – целое число;
p = 0
, где Ц = 1, 2, 3, … – целое число;
p = 0
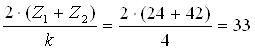 - условие целостности выполняется
- условие целостности выполняется
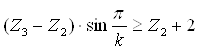 ;
; 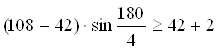
![]() - выполняется.
- выполняется.
Окончательно принимаем Z1 = 24; Z2 = 42; Z3 = 108.
Определяем диаметры колес планетарного редуктора. Редуктор собирается из колес без смещения.
![]()
![]() мм
мм
![]() мм
мм
![]() мм
мм
Вычерчиваем схему редуктора в масштабе 1: 3
3.2 Проектирование цилиндрической эвольвенты зубчатой передачи внешнего зацепления
Исходные данные:
Z1 =13, Z2 =28 – числа зубьев колёс;
m = 8 мм – модуль зацепления;
h*a = 1 – коэффициент высоты головки зуба;
с* = 0,25 – коэффициент радиального зазора.
3.2.1 Выбор коэффициентов смещения x1 и x2 исходного контура
Коэффициенты
смещения ![]() и
и ![]() должны соответствовать
условию: (При отсутствии подрезания зубьев.)
должны соответствовать
условию: (При отсутствии подрезания зубьев.)
x1 ³ xmin1; x2 ³ xmin2
xmin1 и xmin2 определяем по формуле:
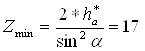 ;
;
Наименьший коэффициент смещения по критерию отсутствия подрезания зуба при заданных числах зубьев:
![]() ;
;
![]() ;
;
Выбираем
коэффициенты смещения ![]() и
и ![]() из таблицы коэффициента смещения
для силовых передач при свободном выборе межосевого расстояния (Z1 = 10…30, Z2 ≤ 30): x1=0.3; x2=0; xå= x1+ x2=0,3.
из таблицы коэффициента смещения
для силовых передач при свободном выборе межосевого расстояния (Z1 = 10…30, Z2 ≤ 30): x1=0.3; x2=0; xå= x1+ x2=0,3.
3.2.2 Угол зацепления 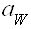
![]() ;
;
aw=22.06160=2204’
3.2.3 Делительные диаметры d1 и d2
d1 = m*z1 = 8*13 = 104 мм
d2 = m*z2 = 18*28 = 224 мм
3.2.8 Радиусы основных окружностей
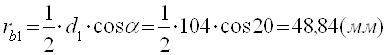 ;
;
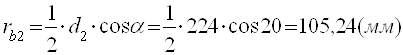 .
.
3.2.4 Делительное межосевое расстояние передачи
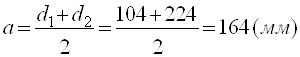
3.2.5 Межосевое расстояние передачи
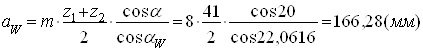
3.2.6 Коэффициент воспринимаемого смещения
![]()
3.2.7 Коэффициент уравнительного смещения
![]()
3.2.8 Радиусы начальных окружностей
![]()
![]()
Проверка вычислений:
aw = rw1 + rw2 = 52.72 + 113.56 = 166.28 (мм)
Радиусы вершин зубьев
![]()
![]()
3.2.9 Радиусы впадин
![]()
![]()
Высота зубьев колес
![]()
h = ra1 – rf1 = ra2 – rf2 = 56,68 – 44,4 = 114,28 – 102 = 12,28 (мм)
Основной делительный шаг зубьев
![]() мм
мм
Относительные толщины зубьев на вершинах в пределах нормы.
Вычерчиваем по полученным данным эвольвенту зубчатого зацепления в масштабе М 2,5: 1.
4. Синтез кулачкового механизма
4.1 Основные положения и определения
Кулачковым механизмом называется трехзвенный механизм, составленный из стойки и двух подвижных звеньев (кулачка и толкателя), связанных между собой посредством высшей кинематической пары. Механизм служит для воспроизведения заданного периодического закона движения ведомого звена. Ведущим звеном в кулачковом механизме является, как правило, кулачок, ведомым звеном толкатель.
Толкатель в кулачковом механизме заканчивается, как правило, вращающимся роликом, который касается кулачка непосредственно. Наличие ролика никак не отражается на законе движения толкателя. Назначение ролика – перевод трения скольжения толкателя по кулачку, в трение качения ролика по поверхности кулачка. В итоге получаем повышение долговечности кулачкового механизма по износу.
Кулачку в кулачковом механизме присущи два профиля – действительный (рабочий) и теоретический.
Действительным профилем является профиль кулачка, с которым непосредственно соприкасается ролик толкателя.
Теоретический профиль – это кривая, которую описывает центр ролика толкателя при движении относительно кулачка.
Действительный и теоретический профили кулачка являются эквидистантными (равноудаленными друг от друга) кривыми.
В движении кулачкового механизма различают в общем случае четыре этапа (фазы):
1 этап – удаление
толкателя, фазовый угол ![]() , 2 этап
– дальнее стояние толкателя, фазовый угол
, 2 этап
– дальнее стояние толкателя, фазовый угол ![]() .
Профиль кулачка на этапе дальнего стояния есть окружность радиуса
.
Профиль кулачка на этапе дальнего стояния есть окружность радиуса ![]() с центром на оси О вращения
кулачка.
с центром на оси О вращения
кулачка.
3 этап – приближение
толкателя, фазовый угол ![]() . 4 этап
– ближнее стояние толкателя, фазовый угол
. 4 этап
– ближнее стояние толкателя, фазовый угол ![]() .
.
Профиль
кулачка на этапе ближнего стояния толкателя, является дугой окружности радиуса ![]() , с центром на оси О
вращения кулачка. При этом
, с центром на оси О
вращения кулачка. При этом ![]() .
.
Соответствие между фазовыми углами в движении кулачка и перемещением толкателя устанавливается, так называемой, циклограммой работы кулачкового механизма.
4.2 Исходные данные
![]() ход толкателя, мм;
ход толкателя, мм;
![]() фазовые углы кулачка, соответствующие
этапам удаления и приближения толкателя, градусы;
фазовые углы кулачка, соответствующие
этапам удаления и приближения толкателя, градусы;
![]() фазовые углы кулачка, соответствующие
дальнему и ближнему стоянию толкателя, градусы;
фазовые углы кулачка, соответствующие
дальнему и ближнему стоянию толкателя, градусы;
Законы движения:
– при удалении: трапецеидальный
– при приближении: параболический симметричный
4.3 Расчет передаточных функций выходного звена
Рассчитаем перемещения Si и аналог ускорения Si¢ по соответствующим заданному закону формулам.
Фаза удаления:
![]() , при
, при ![]()
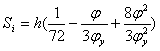 , при
, при ![]()
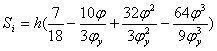 , при
, при ![]()
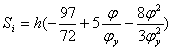 , при
, при ![]()
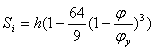 , при
, при ![]()
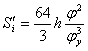 , при
, при ![]()
![]() , при
, при ![]()
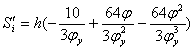 , при
, при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]()
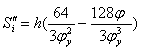 , при
, при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]()
h = 20 (мм); φy = 120º = 2.093 рад; ji=0, 0.348, 0.697, 1.046, 1.395, 1.744, 2.093 рад
Фаза возвращения:
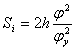 , при
, при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]()
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |