Курсовая работа: Расчет кривошипного механизма

1.3.4. Определение основных размеров маховика

Для определения момента инерции маховика методом исключения параметра j строи зависимость приращения кинетической энергии DТ от приведённого момента инерции звеньев (кривую Виттенбауэра).

Определим углы наклона касательных к кривой Виттенбауэра.

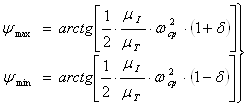       (1.23)

где: wср – частота вращения, мин-1.

mI и mТ – масштабные коэффициенты диаграммы энергомас.

d - коэффициент неравномерности движения (задан в ТЗ).

ymax=0030’ ymin=0020’.

После нахождения углов ymax ymin которые отсчитываем от оси Iпр и проводим две касательные к кривой Виттенбауэра, при этом они ни в одной точке не должны пересекать данную кривую. Касательные на оси DТ отсекают отрезок ав, с помощью которого и находим потребную составляющую приведённого момента инерции обеспечивающая движение звена приведения с заданным коэффициентом неравномерности движения.

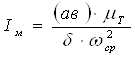           (1.24)

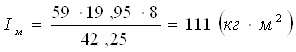
Определяем основные размеры литого маховика по формуле:

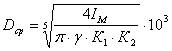   (1.25)

где: Dср – средний диаметр обода маховика;

g - плотность материала маховика, кг/м3;

К1,2- принимаем исходя из конструктивных соображений, с учётом приделов(0,1…0,2). К1,2=0,2.

Определим размеры поперечного сечения обода маховика.

а=К1.Dср; а=0,2.854=170(мм);

в=К2.Dср; в=0,2.854=170(мм).

2.Силовое исследование механизма

Задачей силового исследования рычажного механизма является определение реакций в кинематические парах от действия заданных сил. При этом закон движения начальных звеньев является заданным. Результаты силового исследования применяются при определении: сил трения, возникающих в кинематических парах; геометрических параметров звеньев механизма; мощности, потребляемой механизмом для преодоления внешних сил.

При определении реакций в кинематических парах будем использовать принцип Даламбера, согласно которому звено механизма можно рассматривать как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции. Составим уравнения равновесия, которые называют уравнениями кинетостатики.

В результате движении механизма на его звенья действуют силы: движущие, полезных и вредных сопротивлений, тяжести звеньев, инерции звеньев. Из перечисленных сил нам заданны только силы полезных сопротивлений, а остальные подлежат определению.

Bсe силы инерция звена при его движении сведём к главному вектору сил инерции Fи, проложенному к центру масс эвена, и главному моменту Ми сил инерции.

Сила инерции имеет направление, противоположное ускорению центра масс звена. Момент пары сил инерции направлен противоположно угловому ускорению звена. Ускорения центров масс и угловые ускорения звеньев определяются с помощью планов ускорений.

Строим план механизма в масштабе:

ml=0.003(м/мм).

2.1 Построение плана скоростей

Проводим построение плана скоростей по ранее проделанной методике.

Определим скорость точки А. Зная частоту вращения кривошипа О1А и его длину, определим скорость точки А, используя формулу:

   (2.1)

              (2.2)

где n1 – частота вращения кривошипа.

=6,5(рад/с)

=6,5×0,27=1,76(м/с)

Скорость точки А во всех положениях механизма постоянна, и графически выражается вектором ра.

Определим масштабный коэффициент плана скоростей.

                (2.3)

где ра – отрезок на плане скоростей определяющий скорость точки А, мм.

Дальнейшее построение плана скоростей проводим согласно пункта 1.2, раздела: «Динамический анализ и синтез рычажного механизма».

2.2 Построение плана ускорений

Ускорение точек звеньев механизма определяем с помощью плана ускорений. Запишем полное ускорение точки А.

      (2.4)

Учитывая тот факт, что кривошип вращается с постоянной угловой скоростью то его угловое ускорение аtАО1 равно 0. То есть ускорение точки А состоит только из нормального ускорения, которое направлено по звену к центру вращения кривошипа.

          (2.5)

Определяем масштабный коэффициент плана ускорений.

       (2.6)

Для определения ускорения точки В, принадлежащей звену 3, воспользуемся теоремой о сложении ускорений в переносном и относительном движениях , тогда:

      (2.7)

где:  - нормальное ускорение точки В относительно точки А.

 - тангенциальное ускорение точки В относительно точки А.

аА – ускорение точки А.

 - нормальное ускорение точки В относительно точки О2.

 - тангенциальное ускорение точки В относительно точки О2.

аО2 – ускорение точки О2, равное 0 так как точка О2 неподвижна.

Решив геометрически систему уравнений будем иметь ускорение точки В.

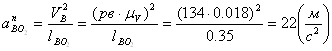
Определим ускорение точки С, для чего составим два векторных уравнения.

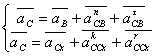       (2.8)

где:  - нормальное ускорение точки С относительно точки В.

 - тангенциальное ускорение точки С относительно точки D.

аВ – ускорение точки В.

 - кориолисово ускорение, определяется поворотом вектора относительной скорости VССx на 90о в сторону угловой скорости звена 4.

 

- релятивное (относительное ) ускорение точки Сx, направлено в вдоль звена 5.

Решив геометрически систему уравнений (2.8) будем иметь ускорение точки С.

2.3 Силовой анализ механизма

Силовое исследование механизма проводим в порядке обратном структурному. Исследование будем проводить без учёта сил трения в кинематических парах. Силы тяжести прикладываем к центру масс.

К диаде (2,3) и (4,5) приложим все силы и момент сил, действующие на неё. Сила сопротивления задана графиком и имеет направление, противоположное рабочему ходу исполнительного органа Величину сил инерции определим по формулам:

         (2.9)

          (2.10)

где: m4 и m5 – массы звеньев 4и5 (кг)

аS4 и (aС=aS5)– ускорение центров масс звеньев (м/с2).

Кроме того на звено 4 действует момент пары сил инерции который имеет направление, противоположно угловому ускорению звена. Его величину определим по формуле:

         (2.11)

где: IS4 – осевой момент инерции звена, кг×м2; e4 – угловое ускорение звена, рад/с2.

      (2,12)

Для определения силы Ft43 составим условие моментного равновесия звена 4.

          (2.13)

Из уравнения (2.13) будем иметь:

   (2.14)

Для определения F50 и Fn43 составим векторное уравнение и строим план сил. Уравнение записываем таким образом чтобы неизвестные реакции стояли по краям уравнения. Для удобства сначала записываем силы, действующие на одно звено, а затем все силы, действующие на другое.

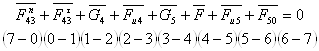  (2.15)

Введём масштабный коэффициент плана сил:

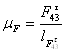      (2.16)

F50=520(H);

Fn43=F43=3000(H);

Рассмотрим диаду 2-3.

Определим силы инерции, действующие на звенья.

         (2.17)

           (2.18)

где: m2 и m3 – массы звеньев 2и3 (кг)

Определим момент пары сил инерции.

Для определения силы Ft21 составим условие моментного равновесия звена 2.

  (2.19)

Из уравнения (2.17) будем иметь:

   (2.20)

Для определения силы Ft30 составим условие моментного равновесия звена 3.

          (2.21)

Из уравнения (2.19) будем иметь:

  (2.22)

Для определения Fn30 и Fn21 составим векторное уравнение и строим план сил. Уравнение записываем таким образом чтобы неизвестные реакции стояли по краям уравнения.

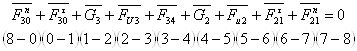    (2.23)

Введём масштабный коэффициент плана сил:

Fn30= F30=4400(H);    Fn21=F21=3200(Н).

2.4 Определение уравновешивающей силы

Определение уравновешивающей силы проводится двумя методами:

Нахождение уравновешивающего момента непосредственно из уравнений равновесия ведущего звена.

Определение уравновешивающей силы и момента с помощью “рычага” Жуковского.

Определим уравновешивающую силу и её момент по первому методу.

Прикладываем к точке А силу F12 равную по модулю ранее найденной силе F21 но противоположную ей по направлению.

Составим уравнение моментов относительно точки О1.

Мур=F12×hF12×ml        (2.24)

Мур=3200×85×0,003=816(Нм)

Определим уравновешивающую силу и её момент с помощью “рычага” Жуковского.

К повёрнутому на 900 плану скоростей в одноимённые точки приложим все силы, действующие на механизм, в том числе и силы инерции. Составим уравнение моментов всех сил относительно полюса плана скоростей с учётом знаков и определим уравновешивающую силу.

Определим расхождение результатов расчёта уравновешивающего момента, полученных выше использованными методами.

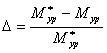       (2.25)

Полученная погрешность составляет 1%, что меньше предельно допускаемого значения в 5%.

3.Синтез кинематической схемы планетарного редуктора и построение картины эвольвентного зацепления

3.1 Задание

3.1.1 Модуль зубчатых колёс планетарного механизма: m1= 3 мм

Числа зубьев колёс простой передачи: Z1=15 , Z2=30;

Модуль зубчатых колёс Z1и Z2: m=6 мм;

Все зубчатые колёса должны быть нулевыми. А это значить, что во избежание подреза ножки зуба для колёс с внешним зацеплением принимают Z>17, для колёс с внутренним зацеплением Z>85.

Подберём числа зубьев Z1,Z2,Z3 для зубчатой передачи с передаточным отношением U=nдв/n1=720/62=11,6.

Задаёмся числом зубьев Z1 из ряда Z1=17,18,19,…. Пусть Z1=20. Число зубьев Z3 найдём из выражения:

           (3.1)

где: U1H – передаточное отношение планетарной передачи входного колеса к выходному звену (водилу) при неподвижном опорном колесе.

          (3.2)

где: Uр – передаточное число одной ступени редуктора.

     (3.3)

      (3.4)

Из формулы (1.1) найдём Z3.

Условие Z3>Zmin=85 выполняется.

Оси центральных колёс и водила должны совпадать между собой, т.е. должно соблюдаться условие соосности, которое имеет вид:

Z1+2Z2=Z3         (3.5)

Из условия соосности находим Z2.

Z2=(Z3-Z1)/2=(96-20)/2=38

Сателлиты должны быть с таким окружным шагом, чтобы между окружностями вершин соседних сателлитов обеспечивался гарантированный зазор- условие соседства:

Sin(1800/k)>(Z2+2)/(Z1+Z2) (3.6)

где: к - число сателитов.

Из условия соседства определяем возможное число сателлитов в механизме.

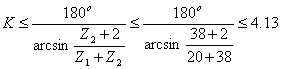
Значит, для этого механизма число сателлитов может быть взято равным 2,3 и 4. Принимаем k=4. Проверяем условие сборки.

Сборка сателлитов должна осуществляться без натягов при равных окружных шагах между ними. Это возможно при выполнении следующего условия:

где: Ц и р целые числа.

        (3.7)

Проверку ведём при р=0.

Условие сборки выполняется т.к. Ц получилось целое число.

Все условия выполняются, значит окончательно принимаем Z1=20; Z2=38; Z3=96; k=4.

Для построения кинематической схемы механизма определим радиусы делительных окружностей.

         (3.8)

  (3.9)

          (3.10)

3.1.2 Расчёт внешнего зацепления пары прямозубых колёс эвольвентных профилей с неподвижными осями, нарезанных стандартной инструментальной рейкой

Окружной шаг по делительной окружности:

Р=p.m        (3.11)

где: m – модуль зубчатой передачи.

Р=3.14.6=18,85(мм)

Угловые шаги:

t=2p/Z        (3.12)

t1=2×3,14/15=0,42        t2=2×3,14/30=0,21

Радиус делительной окружности:

r=0.5m.Z    (3.13)

r1=0.5×6.15=45(мм);     r2=0.5×6.30=90(мм)

Радиус основной окружности:

rв=0.5.m.Z.cosa; (3.14)

где: a - угол профиля рейки rв=0.5.m.Z.cosa;, a=200:

rв1=0.5.6.15.cos20 =42,29(мм) rв2=0.5.6.30.cos20 =84,57 (мм)

Определим относительное смещение инструментальной рейки при нарезании

Х1=Х2=0,5

Толщина зуба по делительной окружности:

S=m(p/2+2x.tga);         (3.15)

S1=6(3.14/2+2×0,5×tg20)=11,61(мм) S2=6(3,14/2+2×0,5×tg20)=11,61(мм);

Инволюта угла зацепления:

invaw= inva + 2[(x1+x2)/(Z1+Z2)]tga;   (3.16)

Invaw= inv20 + 2[(0,5+0,5)/(15+30)]tg20=0,03108;

aw=25017’

Радиус начальной окружности:

rw=0.5m.Z1.cosa/cosaw;      (3.17)

rw1=0.5×6.15.cos20/cos25о17’=46,77(мм) rw2=0.5×6.30.cos20/cos25о17’=93,53(мм);

Межосевое расстояние:

aw=0.5m(.Z1+Z2).cosa/cosaw;       (3.18)

aw=0.5×6×(.15+30).cos20/cos25о17’=140,30(мм);

Радиус окружности впадин:

rf=0.5m(Z1-2.5+2x);     (3.19)

rf1=0.5×6×(15-2.5+2×0.5)=40,5(мм) rf2=0.5×6×(30-2.5+2×0.5)=85,5(мм)

Радиус окружности вершин:

ra1=aw-rf2-0.25m;        (3.20)

ra2=aw-rf1-0.25m;        (3.21)

ra1=140,30-85,5-0.25×6=53,3(м) ra2=140,30-40,5-0.25×6=98,3(мм);

3.1.3 Построение графика коэффициентов относительных скольжений

Теоретическую линию зацепления N1 N2 делим на равные отрезки. По формулам (3.32) и (3.33)определяем величины коэффициентов l1, l2 и сводим в таблицу.

l1=         (3.22)

l2=        (3.21)

U21=Z1/Z2=15/30=0,5;

U12=Z2/Z1=30/15=2.

Таблица 8. Значение коэффициентов l1 и l2.

X	0	24	48	72	96	120	144	168	192	216	240
l1	-¥	-3,50	-1,00	-0,17	0,25	0,5	0,67	0,79	0,88	0,94	1
l2	1	0,78	0,5	0,14	-0,33	-1,0	-2,00	-3,67	-7,00	-17	-¥

По полученным значениям коэффициентов удельных скольжений строим графики.

4. Синтез кулачкового механизма

4.1 Задание

4.1.1 Для построения профиля кулачка достаточно иметь зависимость S= S(j). Для этого дважды проинтегрируем зависимость .

Для получения наглядного результата целесообразно применить метод графического интегрирования зависимости  и .

Заменяя график  ступенчатым, по принципу равенства прибавляемых и вычитаемых площадок с целью выполнения операции графического интегрирования. В результате интегрирования получаем график .

Интегрируя тем же способом график , получаем график .

Определим масштабные коэффициенты для графиков.

Масштаб углов поворота:

mj=;        (4.1)

где: j = jп:

j =60о:

mj==0.25=0.00436

Таблица 9. Значения hS и S,Ls.

Отрезок	hS, мм	S,мм	Ls,мм
0	0	0	0
1	13	1	3
2	46	5	15
3	91	10	30
4	136	15	45
5	170	19	57
6	183	20	60

Введём масштабный коэффициентграфиков.

mS=0.109(м/мм); (4.2)

mS=    (4.3)

  (4.4)

где: Н1,Н2-полюсные расстояния, мм;

Н1=70

Н2=80(мм).

Из 4.3 получаем:

.

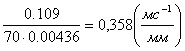Из 4.4 будем иметь:

.

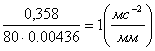4.2.2 Задачей динамического синтеза является определение такого минимального радиуса-вектора Rmin профиля кулачка и такого расстояния d между центрами вращения кулачка и толкателя при наличии которых переменный угол передачи движения ни в одном положении кулачкового механизма не будет меньше gmin

Графическое построение для определения минимального радиуса кулачка будем проводить в масштабе mS. Чтобы определить минимальный радиус кулачка нам нужно построить графики зависимости S-dS/dj. Для этого выберем масштабный коэффициент mS=0,333.

Для определения S и dS/dj воспользуемся формулами:

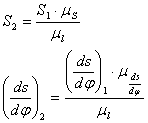        (4.5)

где: S2,S1-расстояния на диаграмме S-dS/dj и S-j соответственно, мм.

(ds/dj)2,(ds/dj)1 – значение скорости на диаграмме S-ds/dj и ds/dj -j, соответственно.

Точка В - центр вращения толкателя. Дуга радиуса lявляется ходом толкателя h= l Sмах. Эта дуга размечена в соответствии с осью ординат диаграммы y-S.

Полученные значения заносим в таблицу- 10

Таблица 10.

отрезок	hdy/dj, мм	ds/dj, мм	l(ds/dj)мм
0	0	0	0
1	42	15	45
2	72	26	78
3	84	30	90
4	72	26	78
5	42	15	45
6	0	0	0

Направление отрезков определяется поворотом вектора скорости точки А толкателя на 90о в сторону вращения кулачка. Через концы этих отрезков проводим прямые образующие с соответствующими лучами углы gmin.

gmin>gдоп; (4.6)

gmin=90о-gдоп

gmin=90о-30о=60о

60о>30о

Rmin=0,042 (м);

4.2.3 Предполагаем, что кулачок вращается противоположно вращению часовой стрелки. Все построения ведём в масштабе:

Для получения практического профиля кулачка нужно построить огибающую дугу радиуса r ролика, имеющих центры на теоретическом профиле.

Для устранения самопересечения профиля кулачка, а также из конструктивных соображений длина r радиуса ролика должна удовлетворять условию:

r <(0.4¸0.5)r0;     (4.7)

где: r0 – минимальный радиус кулачка,r0=0.042(м).

0,042×0,4>0.014;

Принимаем радиус ролика r=0.014(м)=14(мм).