Курсовая работа: Технико-экономическая оптимизация систем теплогазоснабжения (ТЭО)

11. Коэффициент эффективности капитальных вложений Е=0,12 1/год.

Общая длина магистрали.

l=l1+l2+l3=650+550+750=1950 м.

Гидравлическим расчетом Rо=80 кПа , получим следующие диаметры сети по участкам: d1,0=377×9 мм, d2,0=273×7 мм, d3,0=194×5мм.

Материальная характеристика сети.

Мо=0,377·650+0,273·550+0,194·750=540,7 м².

Определим долю потери давления в местных сопротивлениях: m=Z

Определим оптимальное значение удельной линейной потери давления

Определение оптимальной толщины тепловой изоляции трубопроводов тепловой сети.

С увеличением толщины изоляции возрастают затраты в сооружение и эксплуатацию теплоизолированного трубопровода. Вместе с тем, снижается теплопотери, а значит и годовая стоимость теряемой теплоты.

Задача сводится к минимизации функции следующего вида:

З=(Ен+φ)Киз+Итп , (1.3.1)

где Ен – коэффициент эффективности кап вложений 1/год;

φ – доля годовых отчислений на эксплуатацию тепловой изоляции 1/год;

Киз – капитальные вложения в теплоизоляцию 1/год;

Итп – стоимость теплопотерь, руб/год.

Решение задачи рассмотрим на примере двухтрубного подземного теплопровода при бесканальной прокладке.

Капитальные вложения в тепловую изоляцию 1м двухтрубного теплопровода определяется по формуле:

, (1.3.2)

где Сиз – удельная стоимость тепловой изоляции «в деле» , руб/год;

Vиз – объем тепловой изоляции, м;

d – диаметр трубопровода, м;

δиз – толщина тепловой изоляции, м.

Годовая стоимость тепла, теряемого теплопроводом, определяется по формуле

Ит.п = (qп + qо) τ Ст (1+β) , (1.3.3)

где qп , qо - удельные потери тепла 1 м подающего и обратного трубопроводов тепловой сети, Вт/м;

Ст – районные замыкающие затраты на тепловую энергию, руб/(Вт ч);

τ – годовая продолжительность эксплуатации тепловой сети, ч/год;

β - коэффициент, учитывающий теплопотери через не изолированные участки трубопровода.

Удельные теплопотери трубопроводами находятся

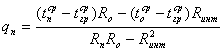, (1.3.4)

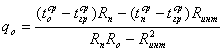, (1.3.5)

где ,-среднегодовая температура теплоносителя в подающей и обратной магистрали, ˚С;

- средняя температура грунта на глубите заложения трубопроводов, принимаются по климатическим справочникам - 5ºС;

Rп, Rо, - термическое сопротивления подающего и обратного трубопроводов тепловой сети, м К/Вт;

Rинт - дополнительное термическое сопротивление, учитывающее тепловую интерференцию теплопроводов, м К/Вт.

Термические сопротивления трубопроводов определяются по формулам:

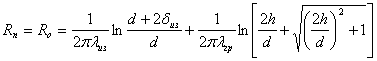, (1.3.6)

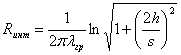, (1.3.7)

где , - теплопроводность теплоизоляции и грунта, Вт/(м К);

h – глубина заложения трубопровода , м;

s – шаг между трубами, м.

Подставляя вышеприведенные выражения в целевую функцию получим (1.3.8)

Задаваясь рядом значений 1,2, …n вычислим затраты З1, З2, …Зn . Условию З=min соответствует оптимальная толщина тепловой изоляции .

Определим оптимальную толщину тепловой изоляции 2х трубного теплопровода водяной теплосети при исходных данных:

1. Прокладка трубопровода – бескональная.

2. Тип тепловой изоляции – битумоперлит.

3. Наружный диаметр трубопровода, dн = 0,219м.

4. Глубина заложения трубопровода , м.

5. Шаг между трубами, ,м.

6. Теплопроводность изоляции, λиз= 0,12 Вт/мк.

7. Теплопроводность грунта, λгр=1,7 Вт/мк.

8. средне годовая температура грунта , = 5ºС.

9. Среднегодовая температура теплоносителя, =90, =50ºС.

10. Годовое число часов работы тепловой сети , τ= 6000 ч/год.

11. Удельная стоимость тепловой изоляцию, Сиз=1330 руб/м3.

12. Удельная стоимость тепловой энергии, СТ=348·руб/(Вт ч).

13. Доля годовых отчислений на эксплуатацию теплоизоляции φ=0,093 1/год.

14. Коэффициент эффективности кап вложений Е=0,12 1/год.

Все расчеты производятся на ЭВМ и результаты заносятся в таблицу 1.

З, руб/год	431	372	339	322	314	313	317	325	336	350	367	386	408	431
,м	0,04	0,06	0,08	0,10	0,12	0,14	0,16	0,18	0,20	0,22	0,24	0,26	0,28	0,30

Минимальному значению удельных приведенных затрат Зmin= 321 руб/(год·м) соответствует оптимальная толщина изоляции = 134 мм. Выявим зону экономической неопределенности управляющего параметра . Для этого примем минимальную погрешность определения расчетных затрат ± 3%. Как видно из графика, наличие погрешности ±ΔЗ обуславливает зону экономической неопределенности управляющего параметра от =86 мм до =192 мм, в пределах которой все значения являются равноэкономичными. Критерию минимума затрат в тепловую изоляцию соответствует =86 мм. Критерию минимума теплопотерь =192 мм.

2. ТЭО СИСТЕМ ГАЗОСНАБЖЕНИЯ.

Выбор оптимальной трассировки межпоселкового распределительного газопровода.

Выбор оптимального варианта трассы сводится к выявлению такого положения головной магистрали, при котором суммарная металлоемкость ответвлений к потребителям имеет минимальное значение. С математической точки зрения, задачи сводятся к нахождению уравнения прямой линии, расположенной на минимальном расстоянии от нескольких случайных точек.

Суть метода заключается в следующем. На генеральном плане местности наносится координатная сетка, на которой фиксируются координаты отдельных потребителей. Поскольку общая металлоемкость ответвлений прямо пропорциональна их суммарной длине и среднему диаметру, при выборе оптимального варианта трассировки головной магистрали необходимо учитывать не только количество и положение потребителей, но их нагрузки.

Для определения расчетных координат головной магистрали распределительного трубопровода используется следующее выражение:

y=a+b·x·Gm , (2.1.1)

где x, y – расчетные координаты магистрали;

a, b – искомые параметры прямой.

Задача заключается в нахождении наименьшей суммы квадратов отклонений расчетных значений координат по уравнению

, (2.1.2)

где n – количество ответвлений к потребителям;

xi, yi – заданные координаты потребителей.

Дифференцируя функцию S по искомым параметрам a и b и приравнивая полученные выражения к нулю, получаем систему следующего вида:

(2.1.3)

решая которую, находим aopt, bopt и оптимальную трассировку трубопровода:

В частном случае, когда нагрузки потребителей одинаковы, целевая функция задачи трансформируется в уравнение

(2.1.4)

Нахождение искомых значений параметров аopt, вopt сводится к решению системы уравнения:

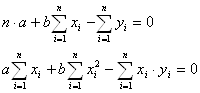(2.1.5)

Необходимо найти оптимальную трассировку межпоселкового газопровода на четыре потребителя со следующими координатами:

x1=2,5 км; y1=8 км;

x2=4,5 км; y2=2,5км;

x3=6,5 км; y3=7,5 км;

x4=10,5 км; y4=7 км.

Нагрузки потребителей одинаковы.

Подставляя координаты в уравнение (2.1.5), получим

4a+b(2,5+4,5+6,5+10,5)-(8+2,5+7,5+7)=0

a(2,5+4,5+6,5+10,5)-b(2,52+4,52+6,52+10,52)-(2,5·8+4,5·2,5+6,5·7,5+10,5·7)=0

После преобразования имеем

4a+24b-25=0

24a+179b-153,5=0

откуда aopt=5,65; bopt=0,1.

Таким образом, оптимальное положение головной магистрали распределительного трубопровода определяется уравнением:

yopt=5,65+0,1x

График полученной зависимости приведен в графической части курсовой работы.

Минимальное расстояние от потребителя до распределительной сети составляет 0,3 м, максимальное – 3,6 м.

Выбор оптимального количества очередей строительства ГРС.

Если строительство объекта осуществляется в течении года и в последующем выходит на проектную эксплуатацию с постоянным уровнем эксплуатационных расходов, годовые приведенные затраты определяются по формуле

З=Ен·к+И , (2.2.1)

где З – приведенные затраты, руб/год;

Ен – нормативный коэффициент эффективности капитальных вложений, 1/год;

к – единовременные вложения в сооружение объекта, руб;

И – текущие издержки по эксплуатации объекта, руб/год.

В том случае, когда капитальные вложения осуществляются в течение нескольких лет, то есть распределены во времени, приведенные затраты определяются с помощью нормативного коэффициента приведения:

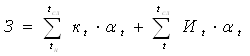, (2.2.2)

где З – суммарные приведенные затраты, руб;

tсл – срок службы объекта;

кt – капитальные вложения в t-том году, руб;

Иt – расходы по эксплуатации в t-том году (без отчислений на реновацию), руб;

αt – коэффициент приведения разновременных затрат базисному году, определяемый по формуле

, (2.2.3)

где Енп – норматив приведения разновременных затрат, равный 0,08;

t – разность мужду годом приведения и базисным годом;

tн – начальный год расчетного периода, определяемый началом финансирования строительства объекта.

В качестве базисного года принимается первый год эксплуатации объекта.

ГРС может быть построена сразу на полную мощность при сметной стоимости к1=2850 тыс. рублей или в две очереди (вторая через 4 года) при сметной стоимости к2=3762 тыс. рублей, в том числе затраты на первую очередь 1180 тыс. рублей. Переменная часть годовых эксплуатационных расходов составляет 5% от соответствующих капитальных вложений. Срок службы станции tсл=25 лет. Необходимо определить экономически более целесообразный вариант строительства.

Расчетные затраты по вариантам определяем, используя формулу (2.2.2):

А) При строительстве ГРС в одну очередь

=2850+131,94+122,17+113,12+104,74+96,98+89,8+83,15+76,99+71,29+66+61,12+56,59+52,4+48,52+44,92+41,59+38,51+35,66+33,02+30,57+28,31+26,21+24,27+22,47+20,81=4371,13 тыс. руб.

Б) При строительстве ГРС в две очереди

=2280+1089,31+105,56+97,74+90,5+138,26+128,02+118,53+109,75+101,62+94,1+87,13+80,67+74,7+69,16+64,04+59,3+54,9+50,84+47,07+43,59+40,36+37,37+34,6+32,04+29,66+27,47=5186,28 тыс.руб.

Вывод: экономически целесообразным является строительство ГРС в одну очередь.

Определение оптимальной мощности и радиуса действия газорегуляторного пункта.

С увеличением радиуса действия ГРП (с уменьшением количества ГРП в жилом массиве) снижаются приведенные затраты по самим ГРП, а так же по распределительным сетям высокого давления. Вместе с тем возрастают затраты в распределительной сети низкого давления за счет увеличения их среднего диаметра. Под радиусом действия ГРП R подразумевают расстояние по прямой от ГРП до точки встречи потоков газа на границе между соседними ГРП. Выявим связь между радиусом действия ГРП R и радиусом действия газопровода Rr. Рассмотрим два варианта размещения ГРП на газоснабжаемой территории: шахматный и коридорный.

В качестве расчетной модели газоснабжаемой территории примем жилой массив с квадратной конфигурацией, с квадратными кварталами и кольцевыми сетями низкого давления.

— - газопровод низкого давления

→ - радиус действия ГРП

● - ГРП

---→ - радиус действия газопровода Rr.

- граница газоснабжаемой территории.

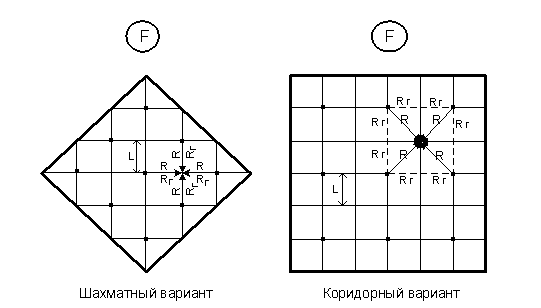
Рис. 2. Схемы размещения ГРС на территории населенного пункта.

Rr=R Rr=R

Rr=L*R L=1/ L=1,3.

Выявим связь между радиусом действия ГРП R, их количеством n и площадью газоснабжаемых территорий F.

R= L , (2.3.1)

L=½ . (2.3.2)

Подставим (2.3.2) в (2.3.1).

, (2.3.3)

. (2.3.4)

Капитальные вложения в ГРП определяются по формуле:

Кгпр = К' · n (2.3.5)

или с учетом (2.3.4)

Кгпр = К'гпр , (2.3.6)

где К'гпр – удельные капитальные вложения в один ГРП, руб.

Затраты по эксплуатации ГРП могут быть выражены в виде годовых отчислений от капитальных вложений.

Игрп=φ·Кгрп (2.3.7)

Приведенные затраты в газорегуляторные пункты с учетом (2.3.6) и (2.3.7) определяются функцией:

Згпр = Ен· Кгпр + Игпр = (Ен + φ) К'гпр (2.3.8)

Определим расчетные затраты в сети низкого давления. Полагаем, что газопроводы работают в режиме гладких труб.

d=a·Q( , (2.3.9)

где d – диаметр газопровода, см;

а – коэффициент пропорциональности, зависящий от состава газа;

Q – расход газа по трубопроводу, м³/ч;

L – длина газопровода, м;

ΔΡ – потеря давления в газопроводе, Па.

Введем подстановку: d = dср; L = Rr = α·R; Q = Qср; ΔΡ = ΔΡн.

получим для среднего диаметра распределительных газопроводов низкого давления

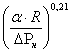dср= a·Qср, (2.3.10)

где ΔΡн – нормативный перепад давлений в уличных распределительных сетях, Па.

Полагаем, что газопроводы несут только путевую нагрузку, можно записать для среднего расхода газа:

Qср=0,55·q· Rr=0,55·q· R·α , (2.3.11)

где q – удельный путевой расход газа, м3/(ч м).

Численные значения указанного параметра определяются по формуле

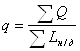, (2.3.12)

где ∑Q – максимальный часовой расход газа жилым массивом;

- суммарная протяженность уличных газопроводов низкого давления.

Подставив (2.3.11) в (2.3.10) и преобразуя полученное выражение, имеем

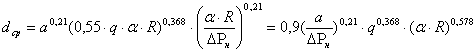(2.3.13)

Удельные капитальные вложения в 1 м газопровода определяются по формуле:

К'н/д=а+в·d , (2.3.14)

где а,в – стоимостные параметры 1 м газопровода, руб/м;

d – диаметр газопровода, см.

Для подземных газопроводов низкого давления допускается применение упрощенной зависимости:

К'н/д ≈в·d (2.3.15)

Общие капитальные вложения в сети низкого давления:

Кн/д= К'н/д (2.3.16)

Расходы на эксплуатацию одного м подземного газопровода низкого давления определяются по формуле:

И'н/д= 0,033К'н/д+0,2 (2.3.17)

Суммарные расходы на эксплуатацию сетей низкого давления:

Ин/д= И'н/д· (2.3.18)

Или с учетом (2.3.13) и (2.3.15)

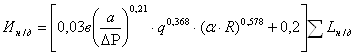(2.3.19)

Приведенные затраты в сети низкого давления

Зн/д = Ен· Кн/д + Ин/д =f(R) (2.3.20)

Определим затраты в сети высокого (среднего) давления. Изменение радиуса действия ГРП мало сказывается но общей конфигурации сети высокого (среднего) давления. В основном изменяется количество и протяженность ответвлений от ГРП к потребителю.

Суммарная протяженность ответвлений определяется количеством ГРП и их радиусом по формуле

(2.3.21)

Капитальные вложения в сети среднего давления:

(2.3.22)

или с учетом (2.3.15)

, (2.3.23)

где dср – средний диаметр ответвлений, см.

Подставив в уравнение (2.3.23) уравнения (2.3.21) и (2.3.4) получим

(2.3.24)

Расходы по эксплуатации одного м газопровода среднего, высокого давления :

И'с/д=0,033Кс/д+0,5 (2.3.25)

Переменная часть эксплуатационных затрат по сетям высокого (среднего) давления

Ис/д = И'с/д (2.3.26)

или с учетом (2.3.15), (2.3.21) и (2.3.4)

(2.3.27)

Переменная часть приведенных затрат по сетям высокого (среднего) давления

Зс/д = Ен· Кс/д + Ис/д (2.3.28)

Подставляя приведенные выражения в исходную целевую функцию получим:

З = Згпр + Зс/д + Зн/д =f(R) (2.3.29)

Для нахождения оптимального радиуса действия ГРП необходимо взять первую производную от затрат и приравнять ее к нулю.

В результате детальной проработки приведенных уравнений получится следующее выражение для оптимального радиуса действия ГРП:

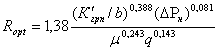, (2.3.30)

где μ – коэффициент плотности сети низкого давления, 1/м;

q – удельная нагрузка сети низкого давления, м3/ч м.

На основании статистического анализа технико-экономических показателей реальных проектов газоснабжения предложены следующие расчетные уравнения:

, (2.3.31)

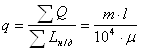, (2.3.32)

где m – плотность населения газоснабжаемой территории, чел/га;

l – удельный часовой расход газа на одного человека, м3/(ч чел);

ΣQ – максимальный часовой расход газа населенным пунктом, м3/ч;

F – площадь газоснабжаемой территории, га.

Положив в уравнении (2.3.30) b=0,55 руб/м см, получим с учетом (2.3.31) и (2.3.32):

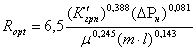(2.3.33)

При известном значении радиуса Ropt оптимальную нагрузку ГРП находим по формуле

(2.3.34)

Оптимальное количество ГПР:

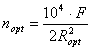(2.3.35)

Определим оптимальный радиус действия, количество и оптимальную пропускную способность ГПР для систем газоснабжения со следующими исходными данными:

1. Стоимость одного ГПР К’гпр =142500 руб.

2. Нормируемый перепад давлений в уличных газопроводах низкого давления ΔΡн=1200 Па.

3. Плотность населения m=684 ч/га.

4. Удельный головной расход газа на отдельного человека l=0,08 м³/(ч чел).

5. Площадь газоснабжаемой территории F=779 га.

Коэффициент плотности сети низкого давления:

μ=(75+0,3·684)10=280,2·10 1/м

Оптимальный радиус действия ГРП:

Оптимальная пропускная способность 1 ГРП:

м³/ч.

Оптимальное количество ГРП:

шт.

Оптимальный радиус действия 1555,3 м, оптимальная пропускная способность 26472,2 м³/ч и оптимальное количество – 2 штук.

Определение оптимальной мощности и радиуса действия газонаполнительной станции сжиженного газа.

Примем в качестве критерия оптимальности минимум удельных приведенных затрат по комплексу ГНС – потребитель:

Згнс-п=Згнс+За.т.+Зпсг=min , (2.4.1)

где Згнс – удельные приведенные затраты по ГНС, руб/т;

За.т – то же в доставку газа автомобильным транспортом, руб/т;

Зпсг – то же в поселковую систему газоснабжения, руб/т.

Поскольку затраты в поселковые системы газоснабжения в сравниваемых вариантах остаются неизменными, примем в качестве целевой функции переменную часть удельных приведенных затрат:

Згнс-п=Згнс+За.т.=min (2.4.2)

Полагая, что потребители сжиженного газа распределены равномерно по всей территории, прилегающей к ГНС, можно записать:

, (2.4.3)

где q – плотность газопотребления на территории, обслуживаемой станцией, т/(год км2);

N – мощность станции, т/год;

F - площадь газоснабжаемой территории, км2.

Связь между мощностью станции и радиусом ее действия устанавливается уравнением:

, (2.4.4)

где R0 – радиус действия станции, км.

Доставка сжиженного газа с населенные пункты осуществляется:

· по кратчайшему расстоянию от ГНС до потребителя (радиальная дорожная сеть);

· по наиболее протяженному маршруту (прямоугольная дорожная сеть).

Рис. 3. Расчетная схема доставки сжиженного газа потребителям.

При среднем варианте доставки продукта

l≈1,2R (2.4.5)

Удельные приведенные затраты в ГНС определяются по формуле:

, (2.4.6)

где А – стоимостной параметр,, численное значение которого зависит от способа реализации сжиженного газа.

Удельные приведенные затраты в автомобильный транспорт сжиженного газа

, (2.4.7)

где а и в – стоимостные параметры, руб/т, численные значения которых зависят от способа доставки сжиженного газа, дорожных условий и других обстоятельств.

Подставив (2.4.5) в (2.4.7) имеем

(2.4.8)

Прирост реализации сжиженного газа соответствует приращению радиуса газоснабжения на величину dR:

Согласно (2.4.8), переменная часть транспортных затрат составляет 1,2вR. Таким образом, общее приращение затрат по доставке сжиженного газа на всей территории, прилегающей к ГНС:

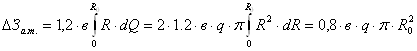, (2.4.9)

где R0 – радиус действия газонаполнительной станции, км, или в перерасчете на 1 т реализуемого газа по (2.4.4)

(2.4.10)

Подставив (2.4.10) в (2.4.8), имеем

(2.4.11)

Тогда с учетом (2.4.6) и (2.4.11) целевая функция задачи (2.4.2) примет следующий вид:

(2.4.12)

Выразим мощность станции через радиус ее действия по уравнению (2.4.4):

(2.4.13)

Для нахождения оптимального радиуса действия ГНС возьмем первую производную от целевой функции и приравняем ее к нулю:

(2.4.14)

откуда

(2.4.15)

а оптимальная мощность станции по (2.4.4) будет

(2.4.16)

Населенный пункт снабжают сжиженным газом от ГНС по следующей схеме:

· 85% квартир – от баллонных установок;

· 15% квартир – от резервуарных установок.

1. Средняя плотность потребления газа на территории, обслуживаемой станцией q= 5 т/(год км2).

2. Удельные экономические показатели баллонных систем газоснабжения Аб=3477000; вб=16,017 руб/(Т км).

3. Удельные экономические показатели резервуарных систем газоснабжения Ар=1858200; вр=3,135 руб/(Т км).

Оптимальный радиус действия ГНС:

· Для баллонного варианта

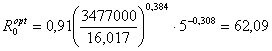км

· Для резервуарного варианта

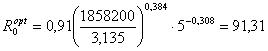км

При заданном соотношении баллонного и резервуарного газоснабжения

км

Оптимальная мощность станции:

тыс.т/год.

Заключение.

В результате технико–экономический расчетов, проведенных по критерию минимума приведенных затрат:

1. Обоснованы оптимальные технические решения и проектные разработки в области ТГС и В, получены оптимальные параметры технологического оборудования, систем и установок.

2. Изучено влияние фактора времени и неопределенности исходной информаций.

3. Проведена экономическая оценка полученных результатов и выявлена экономическая эффективность оптимизации.

Список литературы.

1. Богуславский Л.Д. Экономика теплогазоснабжения и вентиляции. – М.: Стройиздат, 1988. – 351 с.

2. Ионин А.А. Газоснабжение. – М.: Стройиздат, 1989 – 438 с.

3. Ионин А.А., Хлынов Б.М., Братенков В.Н., Терлецная Е.Н. Теплогазоснабжение. – М. Стройиздат 1982 – 162 с.

4. Курицын Б.Н. Оптимизация систем теплогазоснабжения и вентиляции .- Саратов: Издательство СГТУ, 1992 – 162 с.