Курсовая работа: Обработка результатов измерений

Поэтому уравнения системы (2.3.18) иногда называют условными.

Оценим случайную погрешность совместных измерений. Пусть погрешность  имеет нормальный закон распределения с нулевым математическим ожиданием и дисперсией. Измерения  независимы. В этом случае по аналогии с обработкой прямых измерений может быть построена функция максимального правдоподобия:

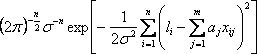  (2.3.21)

Для нахождения экстремума функции правдоподобия (2.3.21) воспользуемся уже известной процедурой. Прологарифмируем (2.3.21) и найдём значения, при которых функция достигает экстремума. Условие максимума функции (2.3.21) является:

 (2.3.22)

Таким образом ((2.3.22)) отвечает требованиям метода наименьших квадратов. Следовательно, при нормальном распределении случайной погрешности оценки по методу максимального правдоподобия и по методу наименьших квадратов совпадает.

Для нахождения оценки  удовлетворяющей (2.3.22) необходимо добиться равенства нулю всех частных производных этой функции по

Для каждого значения  эта оценка будет находиться из следующего уравнения:

 (2.3.23)

Система уравнений (2.3.23) является линейной относительно  и называется системой нормальных уравнений. Число уравнений в системе всегда совпадает с числом .

Система (2.3.23) решается методом определителей

Где D – определитель матрицы  а определитель Dj получается из определителя D заменой j-го столбца столбцом свободных членов.

Для нахождения оценки дисперсии результатов  найдем условие максимума после логарифмирования (2.3.21) и подставим  (см. (2.3.8–2.3.10)), получим:

Построение функциональной зависимости при однофакторном эксперименте

Пусть при однофакторном эксперименте имеется выборка, описывающая изменения входных параметров, и набор выходных величин (рис. 3.1). Необходимо построить зависимость .

Рис. 3.1

Для анализа экспериментальных данных существует очень много способов задания этой зависимости аналитическими и численными методами. Мы отметим лишь самые распространенные из них:

1.  Дальнейшая обработка может проводиться при непосредственном численном использовании массива значений .

2.  2. В случае, когда количество измерений i не слишком велико и разброс значений  мал, зависимость  может быть построена путем интерполяции (аппроксимации) через все экспериментальные точки. В этом случае проводится зависимость  через все точки с координатами . Простейший вариант проведения такой зависимости заключается в построении полинома (степенного ряда).

Пусть  (3.1.1)

Интерполирующая функция

Многочлен  имеет n +1 член.

Требуя выполнения условия (3.1.1), получим систему из  уравнений с  неизвестными:

 (3.1.2)

где каждому  соответствует свое уравнение.

Вместо решения системы уравнений (3.1.2) на практике используются более удобные и менее трудоемкие способы, в частности:

· интерполирование многочленом Лагранжа;

· интерполирование многочленом Ньютона.

Интерполяционные формулы Ньютона особенно удобны в случае равноотстоящих узлов ( одинаково для всех i). В случае, если i велико (большое число узлов), интерполяционный многочлен имеет высокую степень и оказывается неудобным для вычислений.

3.  При слишком высокой степени полинома проблемы можно избежать, разбив отрезок интерполяции на несколько частей с построением для каждой из них своего интерполяционного многочлена. Такое интерполирование имеет серьезный недостаток: в точках стыка интерполяционных многочленов оказывается разрывной первая производная. На рисунке 3.2 показан простейший способ такой интерполяции экспериментальной зависимости – соединение соседних точек прямыми (многочлен степени ).

4. Если необходимо, чтобы зависимость имела непрерывные производные, пользуются сплайнами.

Сплайн (от англ. spline – рейка) – функция, являющаяся алгебраическим многочленом на каждом отрезке  и непрерывная во всей области вместе со своими производными. Чаще всего пользуются сплайнами третьей степени. Соответствующая зависимость показана на рис. 3.2 курсивом.

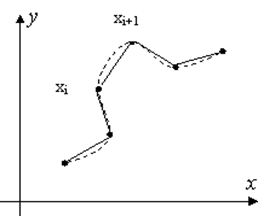
Рис. 3.2.

5. При однофакторном эксперименте, когда имеются результаты многократных измерений со случайной погрешностью (см. параграф 2.2 настоящего пособия), проведение зависимости через все экспериментальные точки бессмысленно. Чаще всего в этом случае для построения функциональной зависимости пользуются методом наименьших квадратов (МНК).

Построение функциональной зависимости при помощи метода наименьших квадратов. Данный метод используется тогда, когда число точек i (узлов) велико и построение плавной зависимости

 (3.1.3)

проходящей через все точки  невозможно из-за большого разброса значений. Функция (3.1.3) называется уравнением регрессии y на x. Пусть приближенная функция, описывающая  зависит от трех параметров  Эта функция не будет проходить через все точки с координатами  тогда можно найти сумму квадратов разностей

 (3.1.4)

Задача сводится к отысканию минимума , т.е. к решению системы уравнений

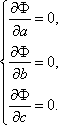 А именно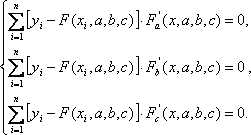

(3.1.5)

Решив систему (3.1.5) относительно параметров a, b, c находим конкретный вид искомой функции.

Приближающая (приближенная) функция может иметь любой вид: линейная зависимость, парабола, синусоида и т.д. Чаще всего используются алгебраические многочлены не выше третьего порядка. В большинстве случаев анализируется линейная регрессия, когда

 (3.1.6)

Главная особенность регрессионного анализа состоит в том, что регрессия y на x не соответствует регрессии x на y (см. рис. 3.3).

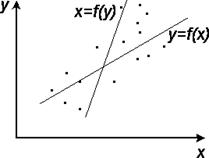
Рис. 3.3.

Поясним это свойство регрессионных зависимостей. Пусть формула регрессии имеет вид (3.1.6), приведем ее обратную функцию:

 (3.1.7)

Обратим внимание, что в (3.1.7) свободный член  зависит от коэффициента наклона a прямой зависимости (3.1.6). При построении же регрессии прямая проходит приблизительно через середину области, охватывающей экспериментальные точки и ее наклон определяется отношением разброса значений по осям x и y (пересечение функций  и  находится в середине области экспериментальных значений). Таким образом, регрессия x(y), построенная по экспериментальным данным, не будет совпадать с (3.1.7) из-за наличия свободного члена.

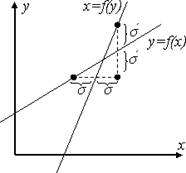
Рис. 3.4

Графически это поясняется на рис. 3.4, где по трем экспериментальным точкам построены регрессии y(x) и x(y), которые не совпадают. Для минимизации СКО трех экспериментальных точек от прямой, зависимость должна проходить через одну из них и в середине между двумя другими точками. Как видно из рис. 3.4, линейные регрессии, построенные из этих соображений пресекаются в центре области экспериментальных значений и имеют разный наклон.

Быстрые методы построения функциональных зависимостей

Задача выбора вида функциональной зависимости – задача неформализуемая, так как одна и та же экспериментальная зависимость может быть описана разными аналитическими выражениями приблизительно с одинаковой точностью. Например, U – образная кривая может быть описана как параболой, так и куском синусоиды.

Основное требование к математической модели – компактность и удобство использования, потому чаще всего пользуются алгебраическими многочленами, экспоненциальными и тригонометрическими функциями. Другое требование – интерпретируемость. Например, если экспериментальная зависимость описывает изменение амплитуды затухающих колебаний, то функциональная зависимость может быть построена в виде  или  В этом случае, из знания природы зависимости (теоретической модели затухающих колебаний), будет выбрана экспоненциальная зависимость .

Погрешность в выборе функциональной зависимости называется погрешностью адекватности модели. Для ее устранения надо рассматривать теоретическую модель описываемого явления или процесса.

Быстрые методы установления графического вида однофакторных зависимостей. Простейший экспресс-метод статистической обработки – метод контура (рис. 3.5, а, б).

Его суть – обведение экспериментальных точек плавными границами. Требование плавности подразумевает, что некоторые точки могут оказаться вне контура (рис. 3.5, а). Метод контура можно использовать тогда, когда разброс экспериментальных точек не слишком велик (рис. 3.5, б).

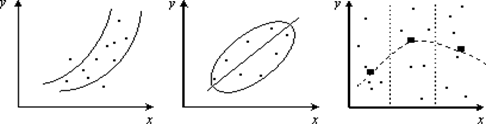
а б в

Рис. 3.5

На рисунке 3.5, в показано построение экспериментальной зависимости более строгим экспресс-методом, – методом медианных центров. Для этого область экспериментальных данных разбивается вертикальными линиями на несколько областей (в данном случае – три области), в каждой из которых находится равное количество экспериментальных точек. Медианными центрами каждой из этих областей по координате x являются точки, справа и слева от которых находится равное количество экспериментальных отсчетов. Найдя таким образом координаты  медианных центров, аналогичным образом в каждой области находят их вертикальные координаты  выше и ниже которых находилось бы равное количество точек. Затем по точкам с координатами  строится плавная экспериментальная кривая. Необходимо помнить, что координаты () медианных центров не совпадают со средними значениями экспериментальных данных.

Связь коэффициента линейной регрессии, коэффициента корреляции и относительной погрешности. Пусть по результатам однофакторного эксперимента строится линейная регрессия  тогда из системы (3.1.5) следует:

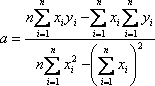
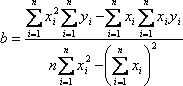  (3.2.1)

С другой стороны коэффициент корреляции, характеризующий связь между  и , по определению

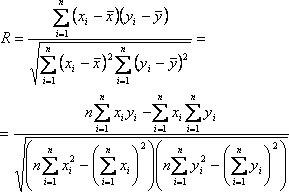 (3.2.2)

Сопоставляя (3.2.1) и (3.2.2), найдем связь между коэффициентом регрессии a и коэффициентом корреляции R:

 (3.2.3)

где  – среднеквадратичные отклонения  и  Таким образом, коэффициент корреляции связан с разбросом значений по осям x, y и определяет возможную степень отклонения линии регрессионной зависимости по наклону. Пусть величина  фиксирована,

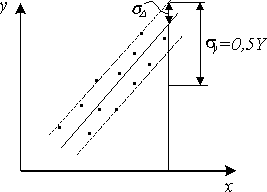
Рис. 3.6

тогда возможное отклонение по оси y от среднего значения  составляет  где  среднеквадратичное отклонение от линии регрессии (см. рис. 3.6). В связи с этим, учитывая (3.2.3), коэффициент корреляции очень часто определяют как

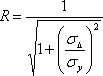 (3.2.4)

где  – ширина полосы погрешностей по y;  – разброс значений  который определяется диапазоном изменения величины .

Поскольку в практических случаях  то формулу (3.2.4) с учетом приближенного разложения до первого члена в ряд Тейлора приводят к виду

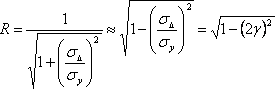 (3.2.5)

Где  приведенная погрешность. Таким образом, в большинстве практических случаев связь между коэффициентом корреляции и приведенной погрешностью может быть установлена при помощи простейшей приближенной формулы (3.2.5).

Быстрая оценка коэффициента корреляции исходных данных. Быструю оценку коэффициента корреляции и погрешности исходных данных можно провести также методом медианных центров (рис. 3.7).

Разобьем поле экспериментальных точек вертикальной чертой на две равные по числу точек области ( точек). В левой и правой частях найдем медианные центры. Проведенная через эти медианные центры, обозначенные звездочкой, прямая a регрессия y на x Теперь разобьем экспериментальную область на равное количество точек по вертикали горизонтальной чертой и, после нахождения соответствующих медианных центров, получим прямую b – регрессию x на y. Прямые a и b совпадут только в том случае, когда коэффициент корреляции между  и  равен единице, то есть R = 1.

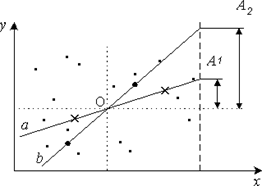
Рис. 3.7

По различию прямых a и b можно с учетом (3.2.3) оценить коэффициент корреляции:

 (3.2.6)

где  определяется отношением углов их наклона. Для быстрой оценки относительной погрешности подставим величину R из (3.2.6) в обращенную формулу (3.2.5):

 (3.2.7)

Таким образом, быстрая оценка коэффициента корреляции и значения относительной погрешности основывается на том, что прямые a и b обязательно проходят через точку пересечения границ О. При этом, чем выше разброс экспериментальных данных (невытянутая область), тем больше будет угол между прямыми a и b.

При построении регрессионных зависимостей методом медианных центров, необходимо помнить, что полученные линии регрессии в общем случае отличаются от соответствующих зависимостей, полученных при помощи МНК. Их различия будут уменьшаться при увеличении количества экспериментальных точек, если разброс экспериментальных данных подчиняется нормальному закону распределения.

Классификация погрешностей измерений

Погрешность средств измерения и результатов измерения. В первую очередь погрешность измерений следует разделить на погрешность средств измерений и погрешность результатов измерений.

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

Погрешность результата измерения – отклонение результата измерения х изм. от действительного (истинного) значения измеряемой величины  определяемая по формуле  – погрешность измерения.

В свою очередь погрешности средств измерений можно разделить на инструментальную и методическую погрешности.

Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности. Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.

Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. Более подробно соотношение между этими погрешностями рассмотрено в главе 4, где описаны виды регистрирующей аппаратуры.

Систематические и случайные погрешности. Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Страницы: 1, 2, 3