Контрольная работа: Электрические цепи постоянного и переменного тока

Далее строится общую ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически "сворачиваем" цепь. Начнем с элемента I1=f(U1) (нэ1), он подсоединен параллельно цепи и его ВАХ будет таким же, как и при дано. Далее делаем характеристики линейного элемента I3=f(U3) и нелинейного элемента (нэ2) I2=f(U2), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I23=f(U23). Затем строим ВАХ нелинейного элемента I1=f(U1) и I23=f(U23), они подсоединены в цепи параллельно, значит, их ток будет равен сумме токов I1=f(U1) и I23=f(U23), значит складываем на графике их общий ток I=f(U).

Дальнейший расчет цепи производим по полученным графикам.

Чтобы найти токи и напряжение на всех элементах цепи поступим так: по оси напряжение находим напряжение равное 200 В (точка а). Из этой точки восстанавливаем перпендикуляр до пересечения I1=f(U1), получаем точку "в". Из точки "в" опустим перпендикуляр на ось тока и получим точку "о", и получим ток (нэ1). Iнэ1=5,2А. Так же восстановим перпендикуляр из точки "а" до пересечение I23=f(U23) и опустим его на ось тока, получим ток во второй ветви I3,не2=I3=Iне2=3А. Отрезке "нд" пересекает ВАХ I3=f(U3) и I2=f(U2) в точках "з" и "г", опустим там перпендикуляры мы получим напряжение на элементах R3 (U3=95В) и (нэ2) (Uнэ2=105В).

2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов в электрических цепях

2.1 Расчет однофазных линейных электрических цепей переменного тока

К зажимам электрической цепи (рис 2.1), подключен синусоидальное напряжение u=54sin(ωt+60º) В частотой f=50Гц.

Выполнить следующее:

1)  определить реактивное сопротивление элементов цепи;

2)  определить действующие значения токов во всех ветвях цепи;

3)  записать уравнение мгновенного значения тока источника;

4)  составить баланс активных и реактивных мощностей;

5)  построить векторную диаграмму токов, совместимую с топографической векторной диаграммой напряжений.

Дано:

R1=10 Ом;

R2=20 Ом;

L1=31,8 мГн;

L2=50,9 мГн;

C1=318 мкФ;

C2=199 мкФ.

Определить: XL1, XL2, XC1, XC2, I, I1, I2, I3, I4, i.

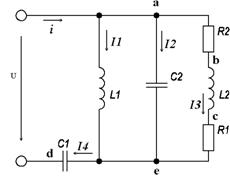
рис 2.1

1) Реактивное сопротивление элементов цепи.

Ом,

Ом,

Ом,

Ом.

2) Расчет токов в ветвях цепи выполнен методом эквивалентных преобразований.

Представим схему, приведенную на рисунке 2.1, в виде:

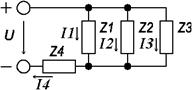
рис 2.2

Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:

Ом;

Ом;

Ом;

Ом;

Ом;

Ом.

Выразим действительное значение напряжение в комплексной форме:

В.

Вычисляем общий ток цепи:

А.

Для определения токов параллельных ветвей I1, I2, I3, рассчитываем напряжение на зажимах:

В

Вычисляем токи ветвей:

А;

А;

А.

3) Уравнение мгновенного значения тока источника:

;

А.

4) Составить баланс активных и реактивных мощностей:

где

Sист=150,488 ВּА,

Pист=122,96 Вт,

Qист= -86,74 вар.

Активная Pпр и реактивная Qпр мощность приемников:

Pпр=I32(R1+R2)=2,032ּ30=123,62 Вт;

Qпр=I12(XL1)+I22(-XC2)+I32(XL2)+I42(-XC1)=6,892ּ10+4,32ּ(-16)+2,032ּ16+3,962ּ(-10)=-88вар

Баланс мощностей выполняется:

Pист=Pпр, Qист=Qпр

123Вт=124Вт, -87вар=-88вар.

Баланс мощностей практически сходится.

5) Напряжения на элементах:

Uab=I3R2=2,03ּ20=40,6 B;	Uae=I2XC1=4,3ּ10=43 B;
Ubc=I3XL2=2,03ּ16=32,48 B;	Ued=IּXC1=3,96ּ16=63,36 B.
Uce=I3R1=2,03ּ10=20,3 B;

6) Строим топографическую векторную диаграмму на комплексной плоскости.

Выбираем масштаб: MI=1 А/см, MU=10 В/см.

Определяем длины векторов токов и напряжений:

см;	см;	см;
см;	см;	см.
см;	см;
см;	см;

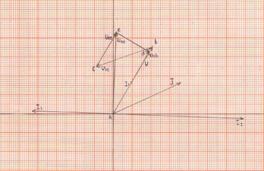
рис 2.3

На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелке, а отрицательные - по часовой стрелке.

Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электрической цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относительно векторов тока: на активном сопротивлении ток и напряжение совпадают по фазе, на индуктивном элементе напряжение опережает ток на 90°, а на емкостном напряжение отстает от тока на 90°.

2.2 Расчет трехфазной линейной цепи переменного тока

В цепи, изображенной на схеме (рис. 2.4), потребители соединены треугольником. Известно линейное напряжение Uл=38 В и сопротивление фаз. RAB=18,8 Ом; RBC=3,8 Ом; RCA=3,1 Ом; XLAB=0,68 Ом; XLAC=2,57 Ом; XCBC=2,2 Ом.

Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.

Дано:

Uл=38 В;

RAB=18,8 Ом;

RCA=3,1 Ом;

XLAB=0,68 Ом;

XLCA=2,57 Ом;

XCBC=2,2 Ом.

Определить: IA, IB, IC, IAB, IBC, ICA, P, Q, S.

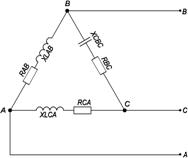
рис 2.4

При соединении трехфазной цепи треугольником расчет будет вести символическим методом.

1) Модули фазных напряжений при соединении треугольником равны линейным напряжениям.

UЛ=UФ=38 В, то есть В

Комплексы данных напряжений запишем из условия, что вектор  совмещен с действующей осью комплексной плоскости;

В;

В;

В.

2) Вычислить комплексы фазных сопротивлений.

Ом,

где

ZAB=2 Ом, φAB=19,9º;

Ом,

где

ZBC=4,82 Ом, φBC=30º;

Ом,

где

ZCA=4,03 Ом, φCA=39,5º.

3) Определить фазные токи:

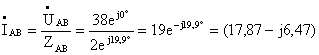А,

модуль IAB=19 А, ψAB=-19,9º;

,

модуль IBC=7,88 А, ψBC=-90º;

А,

модуль ICA=9,43 А, ψCA=80,5º.

4) Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов A, B, C.

А,

модуль IА=22,69 А, аргумент ψА=44º;

А,

модуль IB=17,93 А, аргумент ψB=-4,5º;

A,

модуль IC=17,25 А, аргумент ψC=84,9º.

5) Вычислить мощность каждой фазы и всей цепи:

ВּА,

где

SAB=722 BּA, PAB=679,89 Вт, QAB=-245,75 вар;

ВּА,

где

SВС=299,44 BּA, PBС=-259,32 Вт, QAB=149,72 вар;

ВּА,

где

SCA=360,24 BּA, PCA=-337,43 Вт, QAB=-126,16 вар;

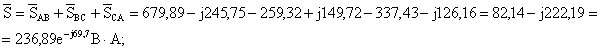
где

S=236,89 BּA, P=82,14 Вт, QAB=-222,19 вар.

6) Строим в масштабе векторную диаграмму напряжений и токов.

Векторы фазных токов , ,  строятся под углами ψAB, ψBC, ψCA к действительной оси. К концам векторов , ,  пристраиваются отрицательные фазные токи согласно уравнениям:

,

,

.

Замыкающие векторные треугольники векторов , ,  представляют в выбранном масштабе линейные токи.

Выбираем масштаб: MI=3 А/см.

см;

см;

см.

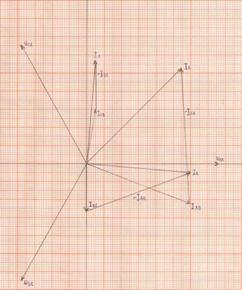
рис 2.5

2.3 Исследование переходных процессов в электрических цепях, содержащих конденсатор и сопротивление

Цепь с последовательно включенными конденсатором емкостью С = 50 мкФ и сопротивлением R = 10 КОм подсоединяется к источнику постоянного напряжения U = 50 В (переключатель в положении 1). Определить законы изменения переходных напряжений и тока при заряде конденсатора и построить их графики. Затем цепь отключается от источника и одновременно переключатель переводится в положение 2. Определить законы изменения переходных напряжений и тока при разряде конденсатора и построить их графики. Определить фактическую длительность заряда и разряда конденсатора и энергию электрического поля при 1 = Зτ. Схема цепи приведена на рис. 2.6.

Дано:

С = 50 мкФ,

R = 10 КОм,

U = 50 В.

Определить: i=f(t),t; uc=f(t),W.

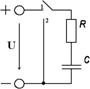
рис 2.6

1) Переключатель в положении 1 (заряд конденсатора)

τ =RּC=104ּ50ּ16-6=0,5c

На основании второго закона коммутации получены законы, характеризующие напряжение и ток при заряде конденсатора.

где U – напряжение источника

uуст=U – установившееся значение напряжения при заряде конденсатора

 – свободная составляющая напряжения при заряде конденсатора.

Зарядный ток равен свободной составляющей, т.к. ток установившегося режима равен 0(iуст=0).

Длительность заряда конденсатора:

t=5τ=5ּ0,5=2,5 с.

Вычисляем значение напряжения на конденсаторе при его заряде для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

t=0, В;

t=τ, B;

t=2τ, B;

t=3τ, B;

t=4τ, B;

t=5τ, B.

Аналогично вычисляем значения зарядного тока согласно закону изменения переходного тока при заряде конденсатора для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

t, c	0	τ	2τ	3τ	4τ	5τ
i, мкА	25	9,19	3,38	1,24	0,46	0,17

Согласно полученным результатам строим графики зарядного напряжения и тока в зависимости от τ. (рис 2.7)

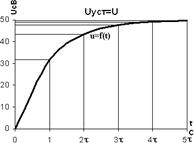
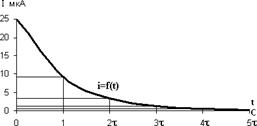
рис 2.7

Из построенных графиков u(t) и i(t) можно для любого момента времени определить значение u и i, а также рассчитать запасенную энергию в электрическом поле заряженного конденсатора.

Например, при t=3τ:

Дж.

2) Переключатель в положении 2 (разряд конденсатора).

Быстрота разряда конденсатора также зависит от параметров цепи и характеризуется постоянной времени, разряда конденсатора:

τ =RC=104ּ50ּ10-6=0,5 с

На основании второго закона коммутации получены законы, характеризующие напряжение и ток при разряде конденсатора:

где U – напряжение заряженного конденсатора до начала разряда.

Разрядные напряжения и ток равны их свободным составляющим, т.к. напряжение и ток установившегося режима после разряда равны 0 (uc уст=0, iуст=0).

Длительность разряда конденсатора:

t=5τ=0,5ּ5=2,5 с.

Вычисляем значения напряжения конденсатора при его разряде для, значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

t=0, В;

t=τ, B;

t=2τ, B;

t=3τ, B;

t=4τ, B;

t=5τ, B.

Аналогично вычисляем значения разрядного тока согласно закону изменения переходного тока при разряде конденсатора для тех же значений времени.

А.

Знак "-" говорит о том, что разрядный ток имеет обратное направление зарядному.

t=0,мкА;

t=τ, мкА;

t=2τ, мкА;

t=3τ, мкА;

t=4τ, мкА;

t=5τ, мкА.

Согласно полученным расчетам строим графики разрядного напряжения и тока в зависимости от τ (рис 2.8).

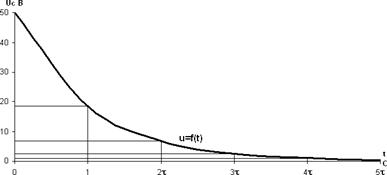
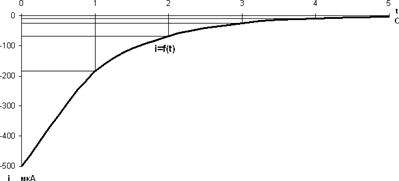
рис 2.8

Энергия электрического поля конденсатора в момент времени t=3τ:

Дж.

Литература

1  Галицкая Л.Н. "Теоретические основы электротехники. Курсовое проектирование" – Минск 1997г.

2  Попов В.С. "Теоретическая электротехника" - Москва 1990г.

3  Евдокимов Ф.Е. "Теоретические основы электротехники". Издательство "Высшая школа" - Москва 2002г.

4  Вычисляем токи ветвей исходной цепи, выполняя алгебраическое сложение частных токов, учитывая их направления.