Курсовая работа: Статистическое изучение результатов деятельности организаций методом группировок

Определим шаг группировки по формуле:

h = ,

где Хmax и Хmin - максимальное и минимальное значение признака

 

 млн. руб.

Обозначим границы групп:

1-я группа - 4667 - 10095,2 (4677+5418,2=10095,2)

2-я группа - 10095,2 - 15513,4 (10095,2+5418,2=15513,4) 3-я группа - 15513,4 - 20931,6 (15513,4+5418,2=20931,6)

4-я группа - 20931,6 - 26349,8 (20931,6+5418,2=26349,8)

5-я группа - 26349,8 - 31768 (26349,8+5418,2=31768)

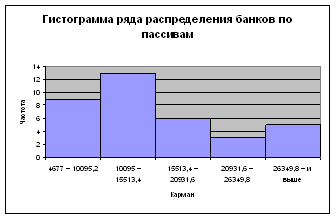
После того как определен группированный признак - пассивы, задано число групп и образованы сами группы, необходимо отобразить ряд распределения.

Таблица 1.3. Ряд распределения предприятий по пассивам

№ п/п	Группы предприятий по пассивам млн. руб.	Число банков в группе	Удельный вес банков группы % (к итогу)
I	4677 - 10095,2	9	25
II	10095 - 15513,4	13	36,1
III	15513,4 - 20931,6	6	16,7
IV	20931,6 - 26349,8	3	8,3
V	26349,8 - и выше	5	13,9
Итого	-	36	100

В данном ряду распределения наиболее многочисленной является вторая группа (13 банков). Наименьшее число банков содержит четвертая группа (3 банка) и по ней наблюдается близкая к средним показателям по пассивам (от 10095 до 15513,4 млн. руб.). Остальные группы по числу входящих в них банков относят к однородным, они содержат по 9, 6 и 5 банков в группе.

Рис 2.

Определим моду

Mo = xo + i * (fмо - fмо-1) / (fмо - fмо-1) + (fмо - fмо+1)

Мо = 10095,2+5418,2* (13-9) / (13-9) + (13+9) = 10897,89 млн. руб.

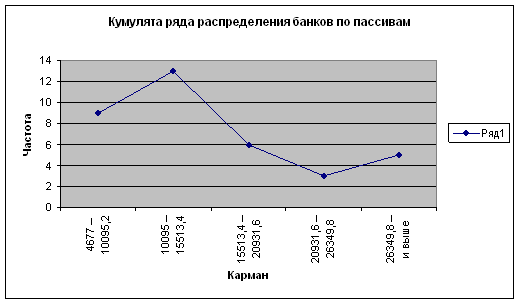
Рис 3

Определим медиану

Me = xo + i * (Σf/2 - Sme-1) / fme

Me = 10095.2+5418.2* (36/2-9) /13 = 13846,261млн. руб.

Рассчитаем среднюю арифметическую по формуле:

X = ,

Где f - частота,

х - середина интервала.

X = = 15513,4 млн. руб.

Рассчитаем среднее квадратическое отклонение

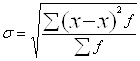
Коэффициент вариации

V=

V=

Так как 46,2% > 33% - это означает, что совокупность неоднородна и средняя величина нетипична для этой совокупности.

При сравнении средней арифметической по исходным данным (10897,89 млн. руб) и средней арифметической, вычисленной по интервальным группам (7167,6 млн. руб) видим разницу между данными показателями 3730,29 млн. руб. Данная неточность возникает за счет того, что при расчете средней арифметической по интервальному ряду делается предположение о равномерности распределения единиц признака внутри группы.

Задание 2.

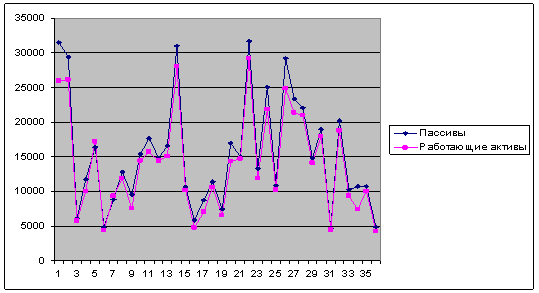
Связь между признаками - пассив и активы.

Определение связи между признаками.

Определим наличие связи между признаками методом аналитической таблицы. Построим аналитическую таблицу.

Таблица 2.1. Аналитическая таблица по сгруппированным данным пассивов

Группы банков по пассивам млн. руб.	Число банков	Пассивы млн. руб.		Работающие активы млн. руб.
		всего	в среднем	всего	в среднем
4677 - 10095,2	9	60848	6761	54230	6026
10095,2 - 15513,4	13	162527	12502	149426	11494
15513,4 - 20931,6	6	106987	17831	98999	16410
20931,6 - 26349,8	3	70465	23488	64207	21402
26349,8 - 31768	5	152954	30591	134284	26857
итого	36	553781	18234,6	501146	16437,8

Определим наличие связи между признаками методом аналитической таблицы. Данные таблицы, представленной в задании 1, показывают, что работающие активы увеличились в среднем в 4,45раз (26857/6026=4,45) от первой группы к пятой, пассивы увеличились в 4,52 раз (30591/6761=4,52)

Это свидетельствует о том, что между рассматриваемыми показателями существует прямая корреляционная связь.

Для того, чтобы определить наличие связи между признаками методом корреляционной таблицы нам необходимо разбить совокупность на группы с равными интервалами по обоим признакам и построить таблицу, в которой необходимо сопоставить эти группы с целью определения сосредоточения частот. Построим группировку по работающим активам. Определим шаг группировки

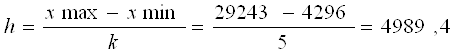 млн. руб.

1-я группа - 4296 - 9285,4 (4296+4989,4)

2-я группа - 9285,4 - 14274,8 (9285,4+4989,4) 3-я группа - 14274,8 - 19264,2 (14274,8 +4989,4)

4-я группа - 19264,2 - 24253,6 (19264,2+4989,4)

5-я группа - 24253,6 - 29243 (24253,6 +4989,4)

Построим корреляционную таблицу

Таблица 2.2. Корреляционная таблица

Группировка банков по активам млн. руб.	Группировка банков по пассивам млн. руб.
	4677 - 10095,2	10095,2 - 15513,4	15513,4 - 20931,6	20931,6 - 26349,8	26349,8 - 31768	∑fу
4296 - 9285,4	9	−	−	−	−	9
9285,4 - 14274,8	−	10	−	−	−	10
14274,8 - 19264,2	−	3	6	−	−	9
19264,2 - 24253,6	−	−	−	3	−	3
24253,6 - 29243	−	−	−	−	5	5
∑fу	9	10	6	3	5	36

Сосредоточение частот по диагонали из левого верхнего угла в правый нижний угол дают возможность предположить о наличии прямой разнонаправленной связи. Рассчитаем тесноту связи между признаками по формулам:

Страницы: 1, 2, 3, 4, 5